机器学习笔记 - 偏最小二乘回归 (PLSR)

发布时间：2024年01月03日

一、偏最小二乘回归：简介

        PLS 方法构成了一个非常大的方法族。虽然回归方法可能是最流行的 PLS 技术，但它绝不是唯一的一种。即使在 PLSR 中，也有多种不同的算法可以获得解决方案。PLS 回归主要由斯堪的纳维亚化学计量学家 Svante Wold 和 Harald Martens 在 20 世纪 80 年代初开发。理论背景基于Herman Wold（Svante 的父亲）的PLS 建模框架。

        偏最小二乘回归（PLSR）是机器学习和预测分析领域的一种流行算法。是一种用于监督学习的降维技术。PLSR是一种在因素较多且高度共线性时构建预测模型的方法。

        它是一种基于回归的方法，旨在找到预测变量空间中解释预测变量和响应之间最大协方差的方向。算法找到与响应变量最密切相关的预测变量的线性组合。该方法在处理大量预测变量时特别有用，因为它有助于降低数据集的维数而不丢失太多信息。

        PLSR 属于监督学习的范畴，这意味着该算法需要标记的训练数据来构建模型。它通常用于生物信息学、化学计量学和金融等领域，这些领域的变量数量通常远大于观测值的数量，并且传统的线性回归模型可能不适合。

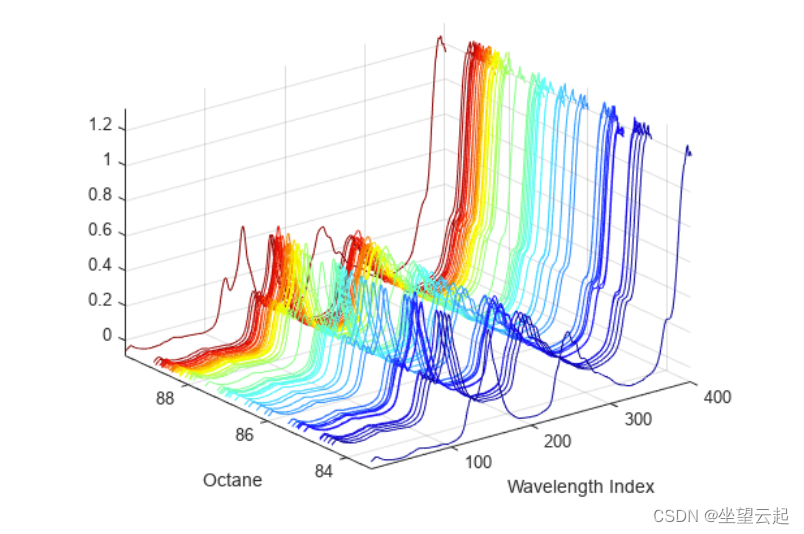
        通过利用 PLSR，工程师和数据科学家可以构建更准确的预测模型，并深入了解具有高

文章来源:https://blog.csdn.net/bashendixie5/article/details/134986140
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章