深度学习 | 深度RNN、Bi-RNN、LSTM、GRU

发布时间：2023年12月27日

?1、深度循环神经网络

1.1、基本思想

????????能捕捉数据中更复杂模式并更好地处理长期依赖关系。

????????深度分层模型比浅层模型更有效率。

????????Deep RNN比传统RNN表征能力更强。

??????? 那么该如何引入深层结构呢？

传统的RNN在每个时间步的迭代都可以分为三个部分：

1.2、三种深层方式

????????

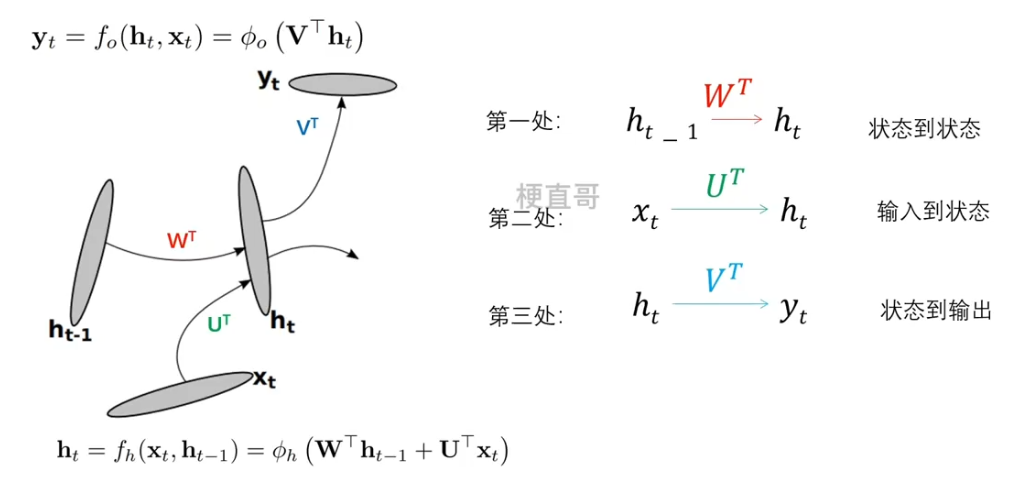
??????? 在传统RNN中，这三处都没有中间层，变换函数都是线性变换紧跟着一个非线性函数，也就是所谓的浅层变换。

??????? 所以就有三种思路，来看看各个思路的变体：

DT-RNN

??????? 这样的好处就是它允许隐变量 ht 适应输入模式 xt 的快速变换，而且它保留了对过去训练的提炼和总结。

??????? 既能适应新变换又不忘初心。这种高度非线性转换可以通过若干个 MLP 全连接层（多层感知机）来实现。

????????

DT(S) - RNN

??????? 由于DT-RNN增加了Loss的梯度，沿着时间反向传播时需要遍历更多的非线性的步数。

????????

DOT-RNN

????????

Stacked RNN

????????????????

模型比较

????????

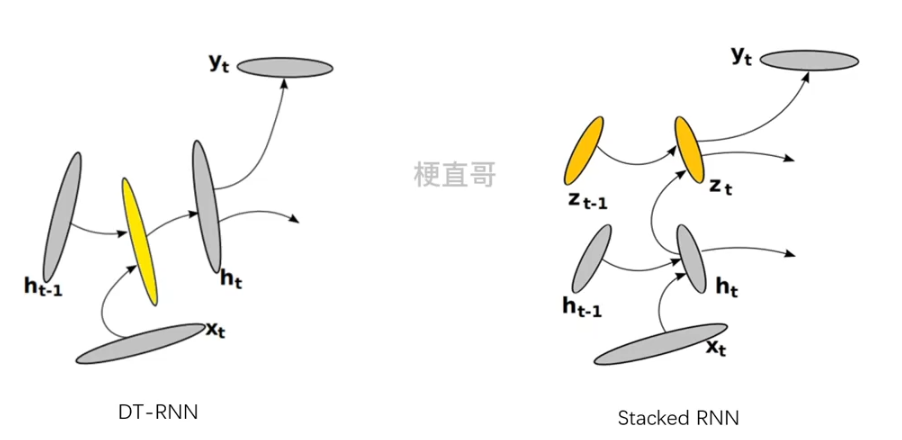
??????? DT-RNN 和 Stacked? RNN 是正交的：

??????? 堆叠的RNN可以出来输入序列中多个时间尺度，而DT-RNN做不到，但是如果将多个DT-RNN堆叠起来，他就可以同时拥有DT-RNN和Stacked RNN 的能力了。

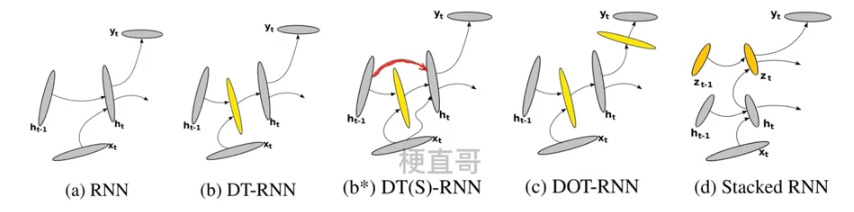
小结

????????在传统RNN的基础上，增加多个浅变换结构的隐藏层，实现对复杂特征更有效的捕捉和处理。

????????

?2、双向循环神经网络

2.1、单向RNN的局限

????????多数RNN只有一个因果结构；

????????许多应用中，输出预测可能依赖整个输入序列；

????????往往需要捕捉序列中上下文之间的关系；

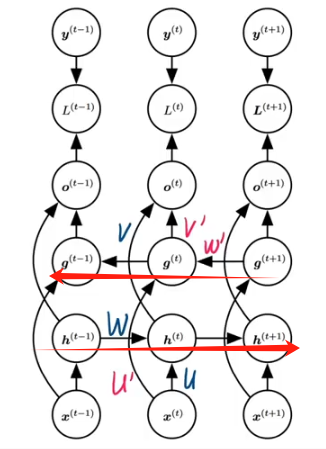
2.2、双向网络结构 —— 两个互相叠加的RNN

???????

??????? 输入不仅取决于先前，还取决于未来。

????????

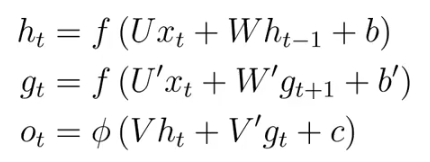
??????? 六个权重矩阵。

????????

?2.3、训练过程

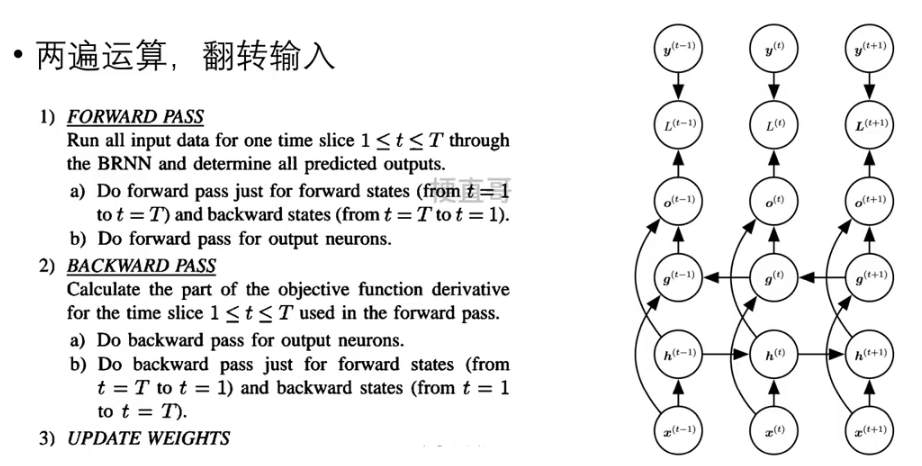
??????? 两遍运算，输入翻转。

?????????

2.4、主要特点分析

????????使用来自序列两端的信息来估计输出；

????????前向传播需要在双向层中进行，反向传播依赖前向传播结果；

????????计算速度慢，梯度求解链很长，训练代价高；

????????主要用于序列编码和双向上下文观测统计。

?3、长短期记忆网络 LSTM

?????????Long-Short Term Memory

?3.1、RNN的问题

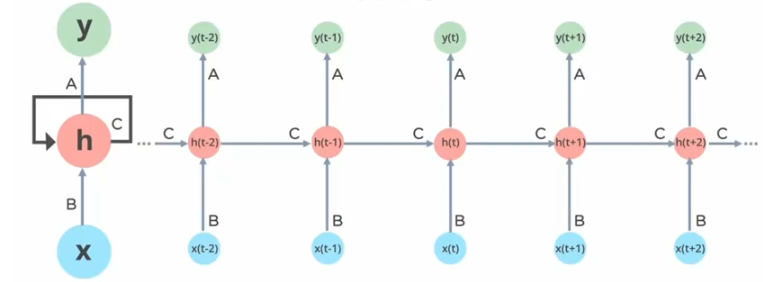
??????? 处理长序列数据时会有梯度消失或爆炸的问题（权重矩阵连乘）

??????? RNN的计算效率相对较低。

????????

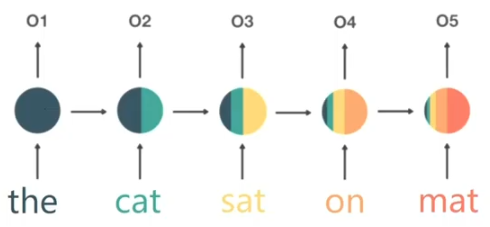
??????? 长时间以前的记忆基本对现在没有什么影响了。

????????

3.2、基本思想

??????? 保留较长序列数据中重要信息，忽略不重要信息。

????????

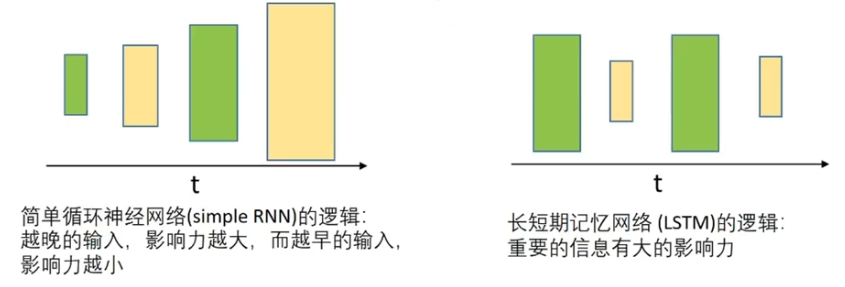
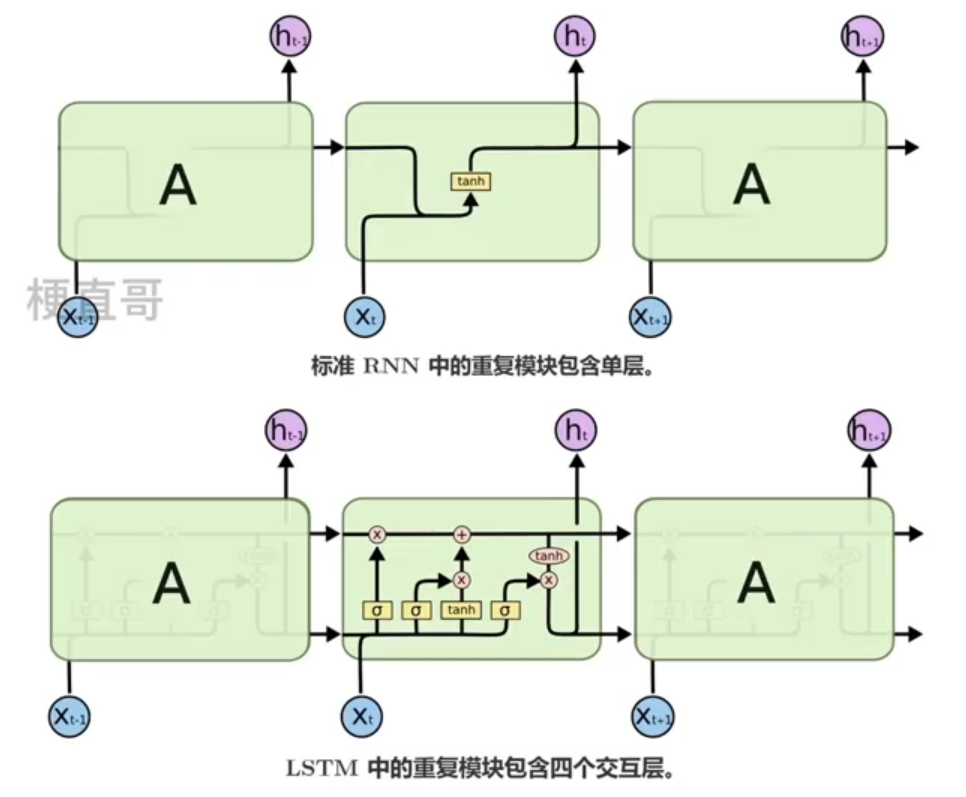
????????RNN都有重复链式结构；

????????标准RNN结构简单；

????????LSTM链式结构特殊；

????????

3.3、门控记忆单元

????????门(gate)控制记忆单元，信息可以沿着这个链条传送。

??????? 原来的RNN隐藏层中只有一个状态 h ，它对短期输入是很敏感的。

??????? 现在人为添加状态 c ，来保持长期记忆。

??????? 打个比方来讲，底下的短期链条相当于时刻发生的事情，上面的链条相当于日记本，记录了长期的记忆 Cells statement 。

??????? 那该怎么控制这种长期的状态 c 呢？

??????? 在任意的时刻 t ，我们需要三件事情：

????????????????t-1 时刻传入的状态 c t-1 中要决定有多少信息需要保留；

??????????????? 当前时刻的输入信息有多少需要传递到 t+1 时刻；

??????????????? 当前时刻的隐层输出 ht 是什么。

??????? ———— LSTM专门设计了 GRU门控记忆单元来控制信息的保留和丢弃。具体来说包括了三种门。每个门就是选择信息通过的方式。

????????

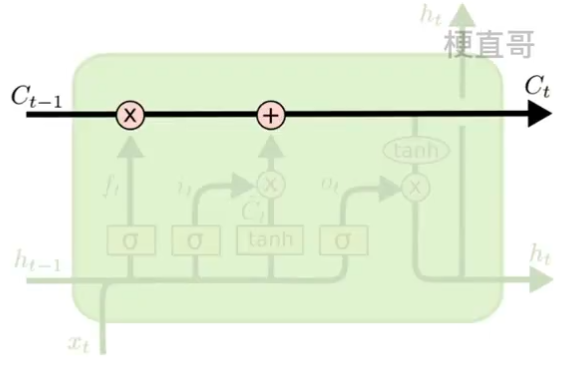
??????? 先来介绍下他们的基本工作原理，之所以称之为门，一定要有一个控制信号，每个门是由一个sigmoid神经网络层以及逐点乘法运算组成的。

????????三个门的作用可以分别理解为：橡皮擦（擦除一些没有用的记忆）、铅笔（写上一些新的记忆）、再输出。

??????? 1、遗忘门（forget gate）

????????????????决定去除那些信息。过滤重要的信息，忽略无关的信息。

??????? ??????? h t-1：上一时刻记忆的状态；

??????????????? x t：当前时间步输入的信息；

??????????????? 这两个的加权和经过一个sigmiod函数，产生遗忘门的输出 f t ，再作用到 c t-1。

????????????????因为 f t 是一个0到1之间的数（橡皮擦），相当于对 c t-1 里面的信息进行了一些选择。

????????????????

??????? 2、输入门（input gate）

????????????????决定什么新的信息将被保留下来。

????????????????在日记本上增加那些记录。

??????????????????????? sigmiod层决定我们将更新哪些值；

??????????????????????? tanh 层创建一个新的候选值向量。

????????????????

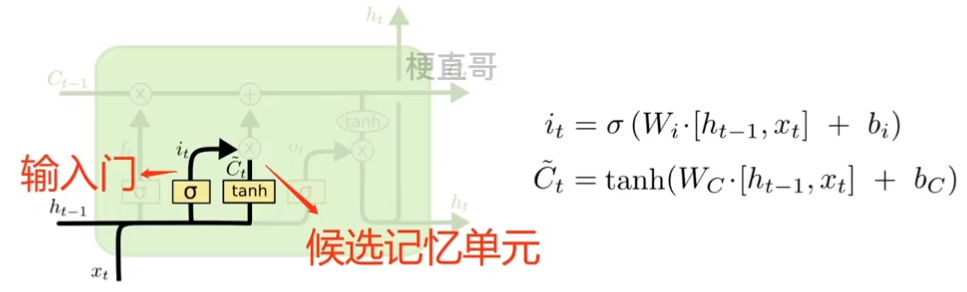
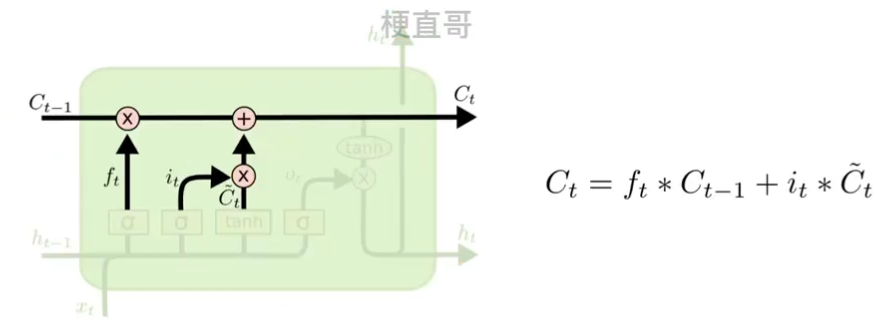
??????? 输入门和候选记忆单元联合更新状态。

????????用橡皮在日记本上删减，再用铅笔添加记录。最后得到了新的长期记忆 c t 。

????????????????

?????????

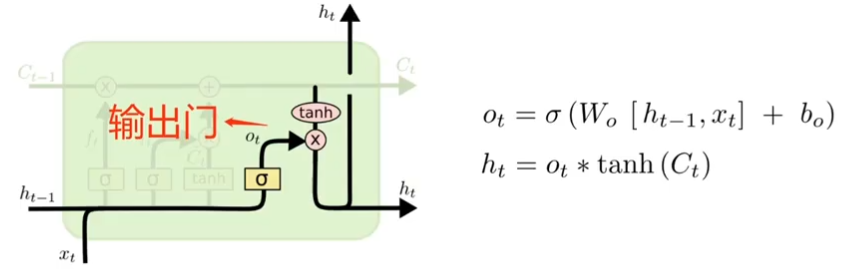
??????? 3、输出门（output gate）

????????????????控制记忆细胞更新时所使用的输入信息。

??????????????? 日记更新当前短期记忆。

???????????????? 控制长期记忆更新并输出给短期记忆 h t 。

???????????????? 先运行一个 sigmoid 层决定要输出 cell 状态的哪些部分 o t （告诉长期记忆哪些部分要去输出）；

?????????????? ? 将cell状态 o t 加上tanh函数之后得到输出 h t 。 tanh函数将c t 值推到 -1 到 1之间。

???????????????

?4、门控循环单元 GRU

?????????Gated Recurrent Unit

??????? 2014年提出，主要针对LSTM模型计算比较复杂容易出现梯度消失或爆炸等问题进行改进。

4.1、与LSTM的区别

????????1、将LSTM原来的三个门简化成为两个：重置门和更新门

????????2、不保留单元状态，只保留隐藏状态作为单元输出

????????3、重置门直接作用于前一时刻的隐藏状态

????????

4.2、基本原理

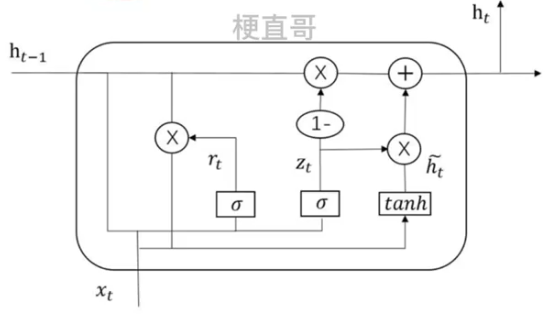
????????引入了两种“门”来控制信息的流动，即重置门(reset gate) 和更新门 (update gate）。

??????? 这两种门都是由一个神经元组成的，通过对输入和上一时刻隐藏状态进行计算来得到当前时刻的输出。

????????

4.2.1、重置门（Reset Gate）

????????用来决定从上一时刻的隐藏状态中“复制”多少信息。

??????? 重置门的输出值在0到1之间，表示从上一时刻的隐藏状态中复制的信息量。

????????

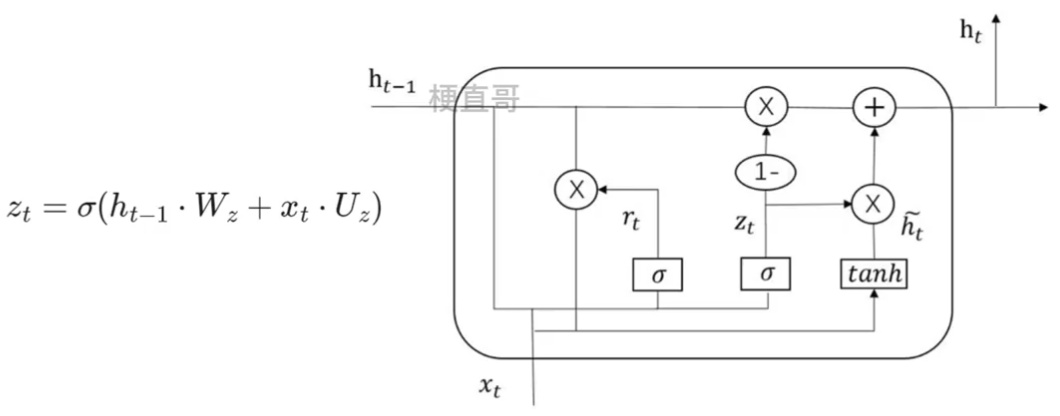
4.2.2、更新门 (Update Gate）

????????用来决定从上一时刻的隐藏状态中“更新”多少信息。

????????

4.2.3、候选隐状态

??????? 候选隐状态是用来计算当前时刻隐藏状态的一个中间结果，将当前时刻的输入与上一时刻隐藏状态结合起来从而得到当前时刻隐藏状态输出 h t 。

??????? 由当前时刻的输入 x t 和上一时刻的隐藏状态 h t-1 通过权重矩阵和偏置向量计算向量得到，并且通过 tanh 函数得到。

??????? 中间小圆圈表示的是元素级别的乘法运算，不同于矩阵乘法。

????????

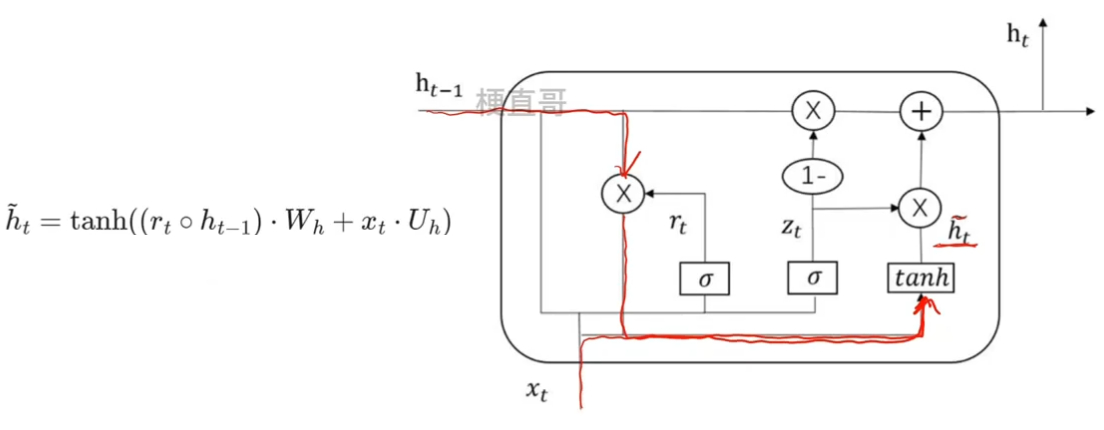
??????? 在计算当前时刻的隐藏状态 h t 时，会与更新门的输出 z t 一起计算，

????????当 z t 比较大时，隐藏状态会更多的使用候选隐状态；反之则使用上一时刻的隐藏状态 h t-1；

4.2.4、隐状态

?????????模型在处理序列数据时记录的当前时刻之前的信息。

???????? 隐状态在计算中主要有两个作用，

??????????????? 1、记录序列数据的上下文信息，帮助模型更好的处理序列数据。

??????????????? 2、控制信息流动，来解决梯度消失和梯度爆炸的问题，提高模型效率。

????????

4.3、计算步骤

??????? 1、计算重置门输出 rt

??????? 2、计算更新门输出 zt

??????? 3、计算候选隐状态（注意私用tanh 和元素级相乘）

??????? 4、计算最终隐藏层输出 ht

????????

5、复杂RNN代码实现

????????DRNN-更深的网络结构

????????BRNN-双向的训练方向

????????LSTM-更强的记忆能力

????????GRU-更简洁而高效

5.1. 模型定义

1.1 深度循环神经网络

from torch import nn
from tqdm import *

class DRNN(nn.Module):
    def __init__(self, input_size, output_size, hidden_size, num_layers):
        super(DRNN, self).__init__()
        self.hidden_size = hidden_size
        self.num_layers = num_layers
        self.rnn = nn.RNN(input_size, hidden_size, num_layers, batch_first=True) 
        # batch_first 为 True时output的tensor为（batch,seq,feature）,否则为（seq,batch,feature）
        self.linear = nn.Linear(hidden_size, output_size)
    
    def forward(self, x):
        # 初始化隐藏状态和细胞状态
        state = torch.zeros(self.num_layers, x.size(0), self.hidden_size)
        # 计算输出和最终隐藏状态
        output, _ = self.rnn(x, state)
        output = self.linear(output)
        return output

# 网络结构
model = DRNN(16, 16, 64, 2)
for name,parameters in model.named_parameters():
    print(name,':',parameters.size())

rnn.weight_ih_l0 : torch.Size([64, 16])
rnn.weight_hh_l0 : torch.Size([64, 64])
rnn.bias_ih_l0 : torch.Size([64])
rnn.bias_hh_l0 : torch.Size([64])
rnn.weight_ih_l1 : torch.Size([64, 64])
rnn.weight_hh_l1 : torch.Size([64, 64])
rnn.bias_ih_l1 : torch.Size([64])
rnn.bias_hh_l1 : torch.Size([64])
linear.weight : torch.Size([16, 64])
linear.bias : torch.Size([16])

1.2 双向循环神经网络

class BRNN(nn.Module):
    def __init__(self, input_size, output_size, hidden_size, num_layers):
        super(BRNN, self).__init__()
        self.hidden_size = hidden_size
        self.num_layers = num_layers
        self.rnn = nn.RNN(input_size, hidden_size, num_layers, batch_first=True, bidirectional=True) # bidirectional为True是双向
        self.linear = nn.Linear(hidden_size * 2, output_size)  # 双向网络，因此有双倍hidden_size
    
    def forward(self, x):
        # 初始化隐藏状态
        state = torch.zeros(self.num_layers * 2, x.size(0), self.hidden_size) # 需要双倍的隐藏层
        output, _ = self.rnn(x, state)
        output = self.linear(output)
        return output

# 网络结构
model = BRNN(16, 16, 64, 2)
for name,parameters in model.named_parameters():
    print(name,':',parameters.size())

rnn.weight_ih_l0 : torch.Size([64, 16])
rnn.weight_hh_l0 : torch.Size([64, 64])
rnn.bias_ih_l0 : torch.Size([64])
rnn.bias_hh_l0 : torch.Size([64])
rnn.weight_ih_l0_reverse : torch.Size([64, 16])
rnn.weight_hh_l0_reverse : torch.Size([64, 64])
rnn.bias_ih_l0_reverse : torch.Size([64])
rnn.bias_hh_l0_reverse : torch.Size([64])
rnn.weight_ih_l1 : torch.Size([64, 128])
rnn.weight_hh_l1 : torch.Size([64, 64])
rnn.bias_ih_l1 : torch.Size([64])
rnn.bias_hh_l1 : torch.Size([64])
rnn.weight_ih_l1_reverse : torch.Size([64, 128])
rnn.weight_hh_l1_reverse : torch.Size([64, 64])
rnn.bias_ih_l1_reverse : torch.Size([64])
rnn.bias_hh_l1_reverse : torch.Size([64])
linear.weight : torch.Size([16, 128])
linear.bias : torch.Size([16])

1.3 长短期记忆网络

class LSTM(nn.Module):
    def __init__(self, input_size, output_size, hidden_size, num_layers):
        super(LSTM, self).__init__()
        self.hidden_size = hidden_size
        self.num_layers = num_layers
        self.lstm = nn.LSTM(input_size, hidden_size, num_layers, batch_first=True) # LSTM
        self.linear = nn.Linear(hidden_size, output_size)
    
    def forward(self, x):
        output, _ = self.lstm(x)
        output = self.linear(output)
        return output

# 网络结构
model = LSTM(16, 16, 64, 2)
for name,parameters in model.named_parameters():
    print(name,':',parameters.size())

lstm.weight_ih_l0 : torch.Size([256, 16])
lstm.weight_hh_l0 : torch.Size([256, 64])
lstm.bias_ih_l0 : torch.Size([256])
lstm.bias_hh_l0 : torch.Size([256])
lstm.weight_ih_l1 : torch.Size([256, 64])
lstm.weight_hh_l1 : torch.Size([256, 64])
lstm.bias_ih_l1 : torch.Size([256])
lstm.bias_hh_l1 : torch.Size([256])
linear.weight : torch.Size([16, 64])
linear.bias : torch.Size([16])

1.4 门控循环单元

class GRU(nn.Module):
    def __init__(self, input_size, output_size, hidden_size, num_layers):
        super(GRU, self).__init__()
        self.hidden_size = hidden_size
        self.num_layers = num_layers
        self.gru = nn.GRU(input_size, hidden_size, num_layers, batch_first=True) # GRU
        self.linear = nn.Linear(hidden_size, output_size)
    
    def forward(self, x):
        output, _ = self.gru(x)
        output = self.linear(output)
        return output

# 网络结构
model = GRU(16, 16, 64, 2)
for name,parameters in model.named_parameters():
    print(name,':',parameters.size())

gru.weight_ih_l0 : torch.Size([192, 16])
gru.weight_hh_l0 : torch.Size([192, 64])
gru.bias_ih_l0 : torch.Size([192])
gru.bias_hh_l0 : torch.Size([192])
gru.weight_ih_l1 : torch.Size([192, 64])
gru.weight_hh_l1 : torch.Size([192, 64])
gru.bias_ih_l1 : torch.Size([192])
gru.bias_hh_l1 : torch.Size([192])
linear.weight : torch.Size([16, 64])
linear.bias : torch.Size([16])

5.2. 模型实验

2.1 数据集加载

import pandas_datareader as pdr
dji = pdr.DataReader('^DJI', 'stooq')
dji

	Open	High	Low	Close	Volume
Date
2023-02-10	33671.54	33897.31	33591.99	33869.27	289863415.0
2023-02-09	34105.61	34252.57	33607.13	33699.88	352340883.0
2023-02-08	34132.90	34161.65	33899.79	33949.01	331798754.0
2023-02-07	33769.78	34240.00	33634.10	34156.69	362844008.0
2023-02-06	33874.44	33962.84	33683.58	33891.02	297051674.0
...	...	...	...	...	...
2018-02-20	25124.91	25179.01	24884.19	24964.75	421529658.0
2018-02-16	25165.94	25432.42	25149.26	25219.38	406774321.0
2018-02-15	25047.82	25203.95	24809.42	25200.37	416778260.0
2018-02-14	24535.82	24925.95	24490.36	24893.49	431152512.0
2018-02-13	24540.33	24705.72	24421.03	24640.45	374415694.0

1258 rows × 5 columns

import matplotlib.pyplot as plt
plt.plot(dji['Close'])
plt.show()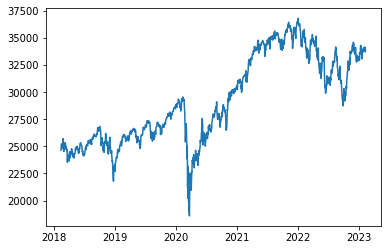

import torch
from torch.utils.data import DataLoader, TensorDataset

num = len(dji)                           # 总数据量
x = torch.tensor(dji['Close'].to_list())  # 股价列表

x = (x - torch.mean(x)) / torch.std(x)

seq_len = 16                               # 预测序列长度
batch_size = 16                            # 设置批大小

X_feature = torch.zeros((num - seq_len, seq_len))      # 构建特征矩阵，num-seq_len行，seq_len列，初始值均为0
Y_label = torch.zeros((num - seq_len, seq_len))        # 构建标签矩阵，形状同特征矩阵
for i in range(seq_len):
    X_feature[:, i] = x[i: num - seq_len + i]    # 为特征矩阵赋值
    Y_label[:, i] = x[i+1: num - seq_len + i + 1]    # 为标签矩阵赋值

train_loader = DataLoader(TensorDataset(
    X_feature[:num-seq_len].unsqueeze(2), Y_label[:num-seq_len]),
    batch_size=batch_size, shuffle=True)  # 构建数据加载器

# 定义超参数
input_size = 1
output_size = 1
num_hiddens = 64
n_layers = 2
lr = 0.001


# 建立模型
model = DRNN(input_size, output_size, num_hiddens, n_layers)
criterion = nn.MSELoss(reduction='none')
trainer = torch.optim.Adam(model.parameters(), lr)

# 训练轮次
num_epochs = 20
rnn_loss_history = []

for epoch in tqdm(range(num_epochs)):
    # 批量训练
    for X, Y in train_loader:
        trainer.zero_grad()
        y_pred = model(X)
        loss = criterion(y_pred.squeeze(), Y.squeeze())
        loss.sum().backward()
        trainer.step()
     # 输出损失
    model.eval()
    with torch.no_grad():
        total_loss = 0
        for X, Y in train_loader:
            y_pred = model(X)
            loss = criterion(y_pred.squeeze(), Y.squeeze())
            total_loss += loss.sum()/loss.numel()
        avg_loss = total_loss / len(train_loader)
        print(f'Epoch {epoch+1}: Validation loss = {avg_loss:.4f}')
        rnn_loss_history.append(avg_loss)
    
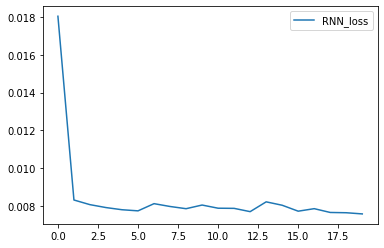
# 绘制损失曲线图
import matplotlib.pyplot as plt
# plt.plot(loss_history, label='loss')
plt.plot(rnn_loss_history, label='RNN_loss')
plt.legend()
plt.show()

  5%|▌         | 1/20 [00:00<00:08,  2.30it/s]Epoch 1: Validation loss = 0.0180

 10%|█         | 2/20 [00:00<00:07,  2.29it/s]Epoch 2: Validation loss = 0.0083

 15%|█▌        | 3/20 [00:01<00:07,  2.29it/s]Epoch 3: Validation loss = 0.0081

 20%|██        | 4/20 [00:01<00:06,  2.29it/s]Epoch 4: Validation loss = 0.0079

 25%|██▌       | 5/20 [00:02<00:06,  2.29it/s]Epoch 5: Validation loss = 0.0078

 30%|███       | 6/20 [00:02<00:06,  2.28it/s]Epoch 6: Validation loss = 0.0077

 35%|███▌      | 7/20 [00:03<00:05,  2.27it/s]Epoch 7: Validation loss = 0.0081

 40%|████      | 8/20 [00:03<00:05,  2.28it/s]Epoch 8: Validation loss = 0.0080

 45%|████▌     | 9/20 [00:03<00:04,  2.28it/s]Epoch 9: Validation loss = 0.0078

 50%|█████     | 10/20 [00:04<00:04,  2.25it/s]Epoch 10: Validation loss = 0.0080

 55%|█████▌    | 11/20 [00:04<00:03,  2.25it/s]Epoch 11: Validation loss = 0.0079

 60%|██████    | 12/20 [00:05<00:03,  2.25it/s]Epoch 12: Validation loss = 0.0079

 65%|██████▌   | 13/20 [00:05<00:03,  2.27it/s]Epoch 13: Validation loss = 0.0077

 70%|███████   | 14/20 [00:06<00:02,  2.25it/s]Epoch 14: Validation loss = 0.0082

 75%|███████▌  | 15/20 [00:06<00:02,  2.26it/s]Epoch 15: Validation loss = 0.0080

 80%|████████  | 16/20 [00:07<00:01,  2.25it/s]Epoch 16: Validation loss = 0.0077

 85%|████████▌ | 17/20 [00:07<00:01,  2.26it/s]Epoch 17: Validation loss = 0.0078

 90%|█████████ | 18/20 [00:07<00:00,  2.28it/s]Epoch 18: Validation loss = 0.0076

 95%|█████████▌| 19/20 [00:08<00:00,  2.28it/s]Epoch 19: Validation loss = 0.0076
100%|██████████| 20/20 [00:08<00:00,  2.27it/s]Epoch 20: Validation loss = 0.0076

rnn_preds = model(X_feature.unsqueeze(2))
rnn_preds.squeeze()
time = torch.arange(1, num+1, dtype= torch.float32)  # 时间轴

plt.plot(time[:num-seq_len], x[seq_len:num], label='dji')
# plt.plot(time[:num-seq_len], preds.detach().numpy(), label='preds')
plt.plot(time[:num-seq_len], rnn_preds[:,seq_len-1].detach(), label='RNN_preds')
plt.legend()
plt.show()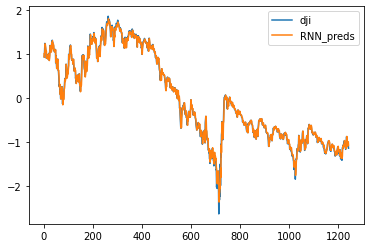

5.3 效果对比

# 定义超参数
input_size = 1
output_size = 1
num_hiddens = 64
n_layers = 2
lr = 0.001


# 建立模型
model_name = ['DRNN', 'BRNN', 'LSTM', 'GRU']
drnn = DRNN(input_size, output_size, num_hiddens, n_layers)
brnn = BRNN(input_size, output_size, num_hiddens, n_layers)
lstm = LSTM(input_size, output_size, num_hiddens, n_layers)
gru = GRU(input_size, output_size, num_hiddens, n_layers)
models = [drnn, brnn, lstm, gru]

opts = [torch.optim.Adam(drnn.parameters(), lr), 
            torch.optim.Adam(brnn.parameters(), lr), 
            torch.optim.Adam(lstm.parameters(), lr), 
            torch.optim.Adam(gru.parameters(), lr)]
criterion = nn.MSELoss(reduction='none')

num_epochs = 20
rnn_loss_history = []
lr = 0.1
for epoch in tqdm(range(num_epochs)):
    # 批量训练
    for X, Y in train_loader:
        for index, model, optimizer in zip(range(len(models)), models, opts):
            y_pred = model(X)
            loss = criterion(y_pred.squeeze(), Y.squeeze())
            trainer.zero_grad()
            loss.sum().backward()
            trainer.step()

100%|██████████| 20/20 [00:59<00:00,  2.95s/it]

for i in range(4):
    rnn_preds = models[i](X_feature.unsqueeze(2))
    bias = torch.sum(x[seq_len:num] - rnn_preds[:,seq_len-1].detach().numpy())
    print ('{} bias : {}'.format(model_name[i],str(bias)))

DRNN bias : tensor(125995.9453)
BRNN bias : tensor(-24902.6758)
LSTM bias : tensor(130150.6797)
GRU bias : tensor(102981.3438)

参考来源

Chapter-10/10.5 复杂循环神经网络代码实现.ipynb · 梗直哥/Deep-Learning-Code - Gitee.com

文章来源:https://blog.csdn.net/weixin_47187147/article/details/135237338
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！

深度学习 | 深度RNN、Bi-RNN、LSTM、GRU

?1、深度循环神经网络

1.2、三种深层方式

DT-RNN

DT(S) - RNN

DOT-RNN

Stacked RNN

?2、双向循环神经网络

2.2、双向网络结构 —— 两个互相叠加的RNN

?3、长短期记忆网络 LSTM

3.3、门控记忆单元

??????? 1、遗忘门（forget gate）

??????? 2、输入门 （input gate）

??????? 3、输出门（output gate）

?4、门控循环单元 GRU

4.2、基本原理

4.2.1、重置门（Reset Gate）

4.2.2、更新门 (Update Gate）

4.2.3、候选隐状态

4.2.4、隐状态

5、复杂RNN代码实现

5.1. 模型定义

1.1 深度循环神经网络

1.2 双向循环神经网络

1.3 长短期记忆网络

1.4 门控循环单元

5.2. 模型实验

2.1 数据集加载

5.3 效果对比

??????? 2、输入门（input gate）