秋招复习之迭代与递归
目录
前言
复习中ing,递归我总是迷迷糊糊的,这里有点醍醐灌顶。迭代是自下而上,从最基础的步骤开始,然后不断重复或累加这些步骤,直到任务完成。递归是自上而下,找到终止条件,然后向上“归”。
之前也刷过类似题:力扣刷题篇之递归-CSDN博客
参考2.2 ? 迭代与递归 - Hello 算法 (hello-algo.com)
递归
「递归 recursion」是一种算法策略,通过函数调用自身来解决问题。它主要包含两个阶段。
- 递:程序不断深入地调用自身,通常传入更小或更简化的参数,直到达到“终止条件”。
- 归:触发“终止条件”后,程序从最深层的递归函数开始逐层返回,汇聚每一层的结果。
而从实现的角度看,递归代码主要包含三个要素。
- 终止条件:用于决定什么时候由“递”转“归”。
- 递归调用:对应“递”,函数调用自身,通常输入更小或更简化的参数。
- 返回结果:对应“归”,将当前递归层级的结果返回至上一层。
观察以下代码,我们只需调用函数?recur(n)?,就可以完成?1+2+?+n 的计算:
/* 递归 */
int recur(int n) {
// 终止条件
if (n == 1)
return 1;
// 递:递归调用
int res = recur(n - 1);
// 归:返回结果
return n + res;
}?该函数的递归过程:

虽然从计算角度看,迭代与递归可以得到相同的结果,但它们代表了两种完全不同的思考和解决问题的范式。
- 迭代:“自下而上”地解决问题。从最基础的步骤开始,然后不断重复或累加这些步骤,直到任务完成。
- 递归:“自上而下”地解决问题。将原问题分解为更小的子问题,这些子问题和原问题具有相同的形式。接下来将子问题继续分解为更小的子问题,直到基本情况时停止(基本情况的解是已知的)。
以上述求和函数为例,设问题
- 迭代:在循环中模拟求和过程,从?1?遍历到?n?,每轮执行求和操作,即可求得?f(n)。
- 递归:将问题分解为子问题?
,不断(递归地)分解下去,直至基本情况?f(1)=1?时终止。
1. ?调用栈
递归函数每次调用自身时,系统都会为新开启的函数分配内存,以存储局部变量、调用地址和其他信息等。这将导致两方面的结果。
- 函数的上下文数据都存储在称为“栈帧空间”的内存区域中,直至函数返回后才会被释放。因此,递归通常比迭代更加耗费内存空间。
- 递归调用函数会产生额外的开销。因此递归通常比循环的时间效率更低。
如图 2-4 所示,在触发终止条件前,同时存在n个未返回的递归函数,递归深度为 n。

在实际中,编程语言允许的递归深度通常是有限的,过深的递归可能导致栈溢出错误。
2. ?尾递归
有趣的是,如果函数在返回前的最后一步才进行递归调用,则该函数可以被编译器或解释器优化,使其在空间效率上与迭代相当。这种情况被称为「尾递归 tail recursion」。
- 普通递归:当函数返回到上一层级的函数后,需要继续执行代码,因此系统需要保存上一层调用的上下文。
- 尾递归:递归调用是函数返回前的最后一个操作,这意味着函数返回到上一层级后,无须继续执行其他操作,因此系统无须保存上一层函数的上下文。
以计算?1+2+?+n?为例,我们可以将结果变量?res?设为函数参数,从而实现尾递归:
/* 尾递归 */
int tailRecur(int n, int res) {
// 终止条件
if (n == 0)
return res;
// 尾递归调用
return tailRecur(n - 1, res + n);
}尾递归的执行过程如图所示。对比普通递归和尾递归,两者的求和操作的执行点是不同的。
- 普通递归:求和操作是在“归”的过程中执行的,每层返回后都要再执行一次求和操作。
- 尾递归:求和操作是在“递”的过程中执行的,“归”的过程只需层层返回。

请注意,许多编译器或解释器并不支持尾递归优化。例如,Python 默认不支持尾递归优化,因此即使函数是尾递归形式,仍然可能会遇到栈溢出问题。
3. ?递归树
当处理与“分治”相关的算法问题时,递归往往比迭代的思路更加直观、代码更加易读。以“斐波那契数列”为例。
Question
给定一个斐波那契数列?0,1,1,2,3,5,8,13,…?,求该数列的第?�?个数字。
设斐波那契数列的第?n个数字为?f(n)?,易得两个结论。
- 数列的前两个数字为?f(1)=0?和?f(2)=1?。
- 数列中的每个数字是前两个数字的和,即?f(n)=f(n?1)+f(n?2)?。
按照递推关系进行递归调用,将前两个数字作为终止条件,便可写出递归代码。调用?fib(n)?即可得到斐波那契数列的第?n?个数字:
/* 斐波那契数列:递归 */
int fib(int n) {
// 终止条件 f(1) = 0, f(2) = 1
if (n == 1 || n == 2)
return n - 1;
// 递归调用 f(n) = f(n-1) + f(n-2)
int res = fib(n - 1) + fib(n - 2);
// 返回结果 f(n)
return res;
}观察以上代码,我们在函数内递归调用了两个函数,这意味着从一个调用产生了两个调用分支。如图所示,这样不断递归调用下去,最终将产生一棵层数为?n?的「递归树 recursion tree」。

从本质上看,递归体现了“将问题分解为更小子问题”的思维范式,这种分治策略至关重要。
- 从算法角度看,搜索、排序、回溯、分治、动态规划等许多重要算法策略直接或间接地应用了这种思维方式。
- 从数据结构角度看,递归天然适合处理链表、树和图的相关问题,因为它们非常适合用分治思想进行分析。
总结
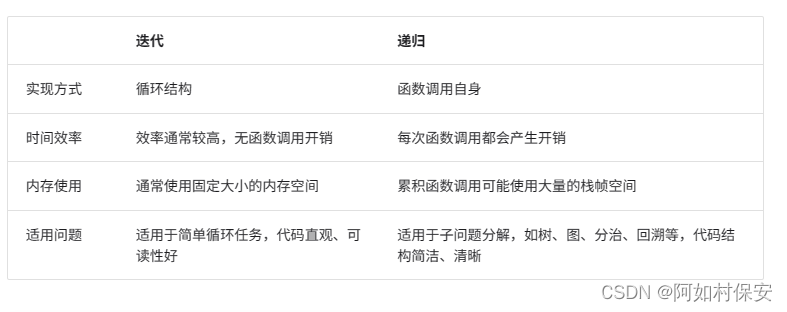
总之,选择迭代还是递归取决于特定问题的性质。在编程实践中,权衡两者的优劣并根据情境选择合适的方法至关重要。?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Python内置类属性__class__属性的使用教程
- 传智杯省赛第一次(C题)
- JAVA毕业设计115—基于Java+Springboot+Vue的教务管理系统(源代码+数据库)
- CRM管理系统好用与否,看这五点!
- 学习笔记|电动汽车上CAN报文解析
- 寒假冬令营(算法编程)1月12日(字符串)
- SpringBoot+FastJson 优雅的过滤 Response Body
- alist(docker版本)挂载百度网盘
- 【数据结构——二叉树】二叉树及其应用2023(头歌习题)【合集】
- 论文阅读 BERT GPT - transformer在NLP领域的延伸