【算法专题】记忆化搜索

什么是记忆化搜索呢？记忆化搜索其实就是带了"备忘录"的递归，给递归加上一个"备忘录"，递归每次返回的时候，将结果放到"备忘录"里面，在每次进入递归的时候，往"备忘录"里面看看，当前需要递归的数据时候在"备忘录"里存在，如果存在，那么就可以直接取此次的结果，不用进行这次的递归。

下面我们看一道经典的递归题可以使用记忆化搜索优化：

1. 斐波那契数(记忆化搜索)

题目链接 -> Leetcode -509.斐波那契数(记忆化搜索)

Leetcode -509.斐波那契数(记忆化搜索)

题目：斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1
给定 n ，请计算 F(n) 。

示例 1：
输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1

示例 2：
输入：n = 3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2

示例 3：
输入：n = 4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3

提示：

• 0 <= n <= 30

思路：记忆化搜索：

• 加上一个"备忘录"；
• 每次进入递归的时候，去"备忘录"里面看看；
• 每次返回的时候，将结果加入到"备忘录"里面；

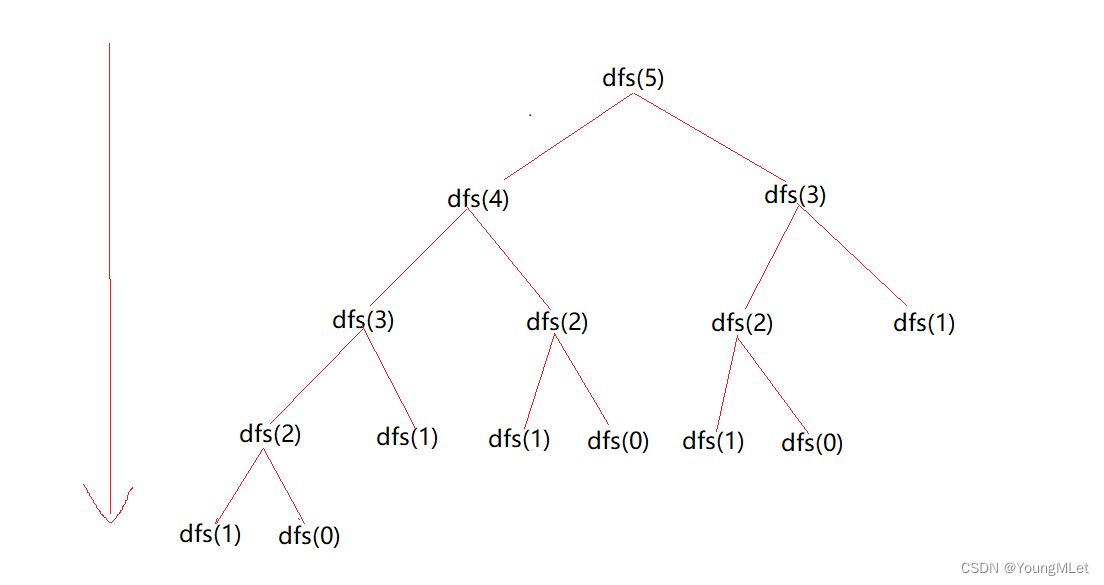
我们可以尝试画图分析一下，假设我们需要求斐波那契的第5个数，假设为 dfs(5)：

如果我们是用暴搜的思路，那么必须是要遍历完整棵树了，如下图，求 dfs(5) 就必须要求 dfs(4) 和 dfs(3)，要得到 dfs(4) 就必须求 dfs(3) 和 dfs(2) …… 以此类推下去：

但是使用记忆化搜索之后，假设当我们求出 dfs(3)，我们就把 dfs(3) 放入"备忘录"，以后如果有需要求 dfs(3) 的时候，我们就往这个"备忘录"上看看是否存在 dfs(3)，如果存在就直接取数据即可；如下图，红框中的数据就是直接从"备忘录"中取即可，因为已经求过了：

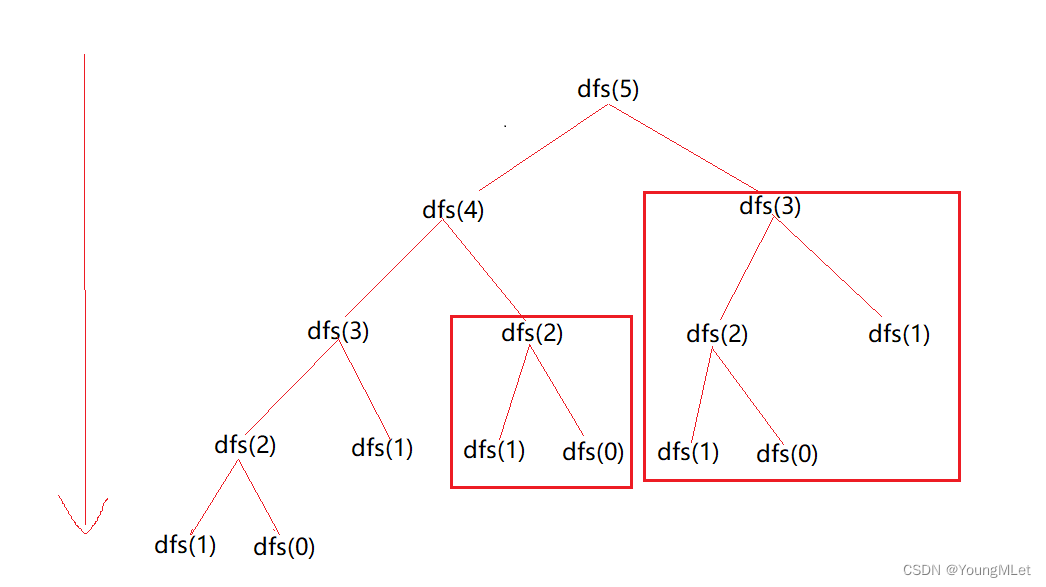
代码如下：

		class Solution 
		{
		public:
		    // 记忆化搜索
		    // 使用一个数组记录已经计算过的值
		    int fib(int n) 
		    {
		        vector<int> memo(31, -1);
		        return dfs(n, memo);
		    }
		
		    int dfs(int n, vector<int>& memo)
		    {
		        if(memo[n] != -1) return memo[n];
		
		        if(n == 0 || n == 1)
		        {
		            memo[n] = n;
		            return n;
		        }
		
		        return dfs(n - 1, memo) + dfs(n - 2, memo);
		    }
		};

2. 不同路径Ⅱ(记忆化搜索)

题目链接 -> Leetcode -62.不同路径Ⅱ(记忆化搜索)

Leetcode -62.不同路径Ⅱ(记忆化搜索)

题目：一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：
输入：m = 3, n = 7
输出：28

示例 2：
输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右->向下->向下
2. 向下->向下->向右
3. 向下->向右->向下

示例 3：
输入：m = 7, n = 3
输出：28

示例 4：
输入：m = 3, n = 3
输出：6

提示：

• 1 <= m, n <= 100
• 题目数据保证答案小于等于 2 * 10^9

思路：记忆化搜索：

• 加上一个备忘录；
• 每次进入递归的时候，去备忘录里面看看；
• 每次返回的时候，将结果加入到备忘录里面；

有了第一题的经验我们直接创建一个"备忘录"即可。

代码如下：

		class Solution 
		{
		    // 记忆化搜索
		public:
		    int uniquePaths(int m, int n) 
		    {
		        // "备忘录"
		        vector<vector<int>> memo(m, vector<int>(n));
		        return dfs(m - 1, n - 1, memo); 
		    }
		
		    int dfs(int m, int n, vector<vector<int>>& vv)
		    {
		        // 如果"备忘录"中有数据，则直接返回
		        if(vv[m][n] != 0) return vv[m][n];
		
		        // 第一个位置
		        if(m == 0 && n == 0) 
		        {
		            vv[m][n] = 1;
		            return 1;
		        }
		
		        // 只能往右走
		        else if(m == 0) 
		        {
		            vv[m][n] = dfs(m, n - 1, vv);
		            return vv[m][n];
		        }
		
		        // 只能往下走
		        else if(n == 0) 
		        {
		            vv[m][n] = dfs(m - 1, n, vv);
		            return vv[m][n];
		        }
		
		        else 
		        {
		            vv[m][n] = dfs(m, n - 1, vv) + dfs(m - 1, n, vv);
		            return vv[m][n];
		        }
		    }
		};

3. 最长递增子序列(记忆化搜索)

题目链接 -> Leetcode -300.最长递增子序列

Leetcode -300.最长递增子序列

题目：给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。
例如，[3, 6, 2, 7] 是数组[0, 3, 1, 6, 2, 2, 7] 的子序列。

示例 1：
输入：nums = [10, 9, 2, 5, 3, 7, 101, 18]
输出：4
解释：最长递增子序列是[2, 3, 7, 101]，因此长度为 4 。

示例 2：
输入：nums = [0, 1, 0, 3, 2, 3]
输出：4

示例 3：
输入：nums = [7, 7, 7, 7, 7, 7, 7]
输出：1

提示：

• 1 <= nums.length <= 2500
• -10^4 <= nums[i] <= 10^4

思路：记忆化搜索：

• 加上一个"备忘录"；
• 每次进入递归的时候，去"备忘录"里面看看；
• 每次返回的时候，将结果加入到"备忘录"里面；

代码如下：

		class Solution {
		public:
		    int lengthOfLIS(vector<int>& nums)
		    {
		        // 记忆化搜索
		        vector<int> memo(nums.size());
		        int ret = 0;
		        for(int i = 0; i < nums.size(); i++)
		        {
		            ret = max(dfs(i, nums, memo), ret);
		        }
		        return ret;
		    }
		
		    int dfs(int start, vector<int>& nums, vector<int>& memo)
		    {
		    	// 如果"备忘录"中没有，则开始计算以当前位置开始的最长递增子序列
		        if (memo[start] == 0)
		        {
		            int ans = 1;
		            for (int i = start + 1; i < nums.size(); i++)
		            {
		                if (nums[i] > nums[start])
		                {
		                    ans = max(ans, dfs(i, nums, memo) + 1);
		                }
		            }
		            memo[start] = ans;
		            return ans;
		        }
		        return memo[start];
		    }
		};

4. 猜数字大小Ⅱ

题目链接 -> Leetcode -375.猜数字大小Ⅱ

Leetcode -375.猜数字大小Ⅱ

题目：我们正在玩一个猜数游戏，游戏规则如下：

我从 1 到 n 之间选择一个数字。
你来猜我选了哪个数字。
如果你猜到正确的数字，就会 赢得游戏 。
如果你猜错了，那么我会告诉你，我选的数字比你的 更大或者更小 ，并且你需要继续猜数。
每当你猜了数字 x 并且猜错了的时候，你需要支付金额为 x 的现金。如果你花光了钱，就会 输掉游戏 。
给你一个特定的数字 n ，返回能够 确保你获胜 的最小现金数，不管我选择那个数字 。

示例 1：

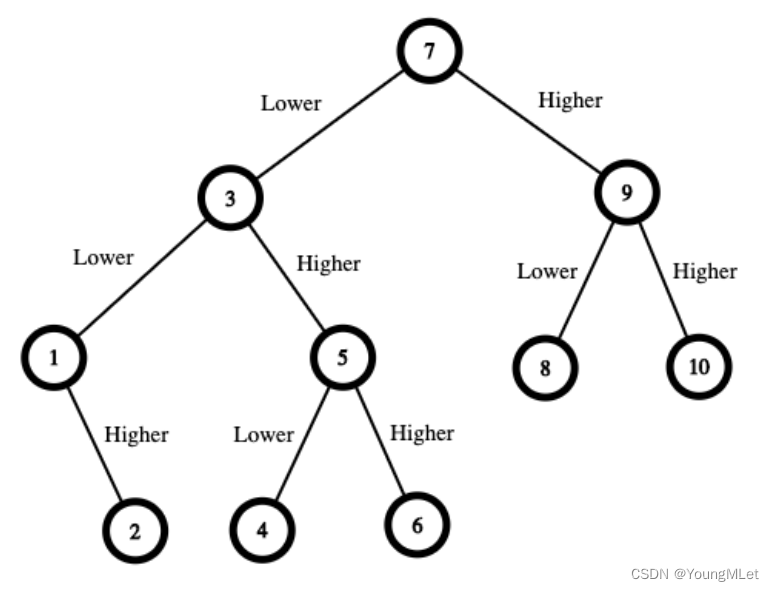
输入：n = 10
输出：16
解释：制胜策略如下：

• 数字范围是[1, 10] 。你先猜测数字为 7 。
• • 如果这是我选中的数字，你的总费用为 $0 。否则，你需要支付 $7 。
• • 如果我的数字更大，则下一步需要猜测的数字范围是[8, 10] ；你可以猜测数字为 9 。
• • • 如果这是我选中的数字，你的总费用为 $7 。否则，你需要支付 $9 。
• • • 如果我的数字更大，那么这个数字一定是 10 。你猜测数字为 10 并赢得游戏，总费用为 $7 + $9 = $16 。
• • • 如果我的数字更小，那么这个数字一定是 8 。你猜测数字为 8 并赢得游戏，总费用为 $7 + $9 = $16 。
• • 如果我的数字更小，则下一步需要猜测的数字范围是[1, 6] 。你可以猜测数字为 3 。
• • • 如果这是我选中的数字，你的总费用为 $7 。否则，你需要支付 $3 。
• • • 如果我的数字更大，则下一步需要猜测的数字范围是[4, 6] 。你可以猜测数字为 5 。
• • • • 如果这是我选中的数字，你的总费用为 $7 + $3 = $10 。否则，你需要支付 $5 。
• • • • 如果我的数字更大，那么这个数字一定是 6 。你猜测数字为 6 并赢得游戏，总费用为 $7 + $3 + $5 = $15 。
• • • • 如果我的数字更小，那么这个数字一定是 4 。你猜测数字为 4 并赢得游戏，总费用为 $7 + $3 + $5 = $15 。
• • • 如果我的数字更小，则下一步需要猜测的数字范围是[1, 2] 。你可以猜测数字为 1 。
• • • • 如果这是我选中的数字，你的总费用为 $7 + $3 = $10 。否则，你需要支付 $1 。
• • • • 如果我的数字更大，那么这个数字一定是 2 。你猜测数字为 2 并赢得游戏，总费用为 $7 + $3 + $1 = $11 。

在最糟糕的情况下，你需要支付 $16 。因此，你只需要 $16 就可以确保自己赢得游戏。

示例 2：
输入：n = 1
输出：0
解释：只有一个可能的数字，所以你可以直接猜 1 并赢得游戏，无需支付任何费用。

示例 3：
输入：n = 2
输出：1
解释：有两个可能的数字 1 和 2 。

• 你可以先猜 1 。
• 如果这是我选中的数字，你的总费用为 $0 。否则，你需要支付 $1 。
• 如果我的数字更大，那么这个数字一定是 2 。你猜测数字为 2 并赢得游戏，总费用为 $1 。

最糟糕的情况下，你需要支付 $1 。

提示：

• 1 <= n <= 200

思路：记忆化搜索：

• 加上一个备忘录；
• 每次进入递归的时候，去备忘录里面看看；
• 每次返回的时候，将结果加入到备忘录里面；

代码如下：

		class Solution 
		{
		    // 记忆化搜索
		    int memo[201][201];
		public:
		    int getMoneyAmount(int n) 
		    {
		        // 返回 1 到 n 区间内能够确保获胜的最小现金数
		        return dfs(1, n);
		    }
		
		    int dfs(int left, int right)
		    {
		        // 非法区间和只有一个数的区间
		        if(left >= right) return 0;
		
		        if(memo[left][right] != 0) return memo[left][right];
		
		        int ret = INT_MAX;
		
		        // 在当前区间内再依次取头节点分区间
		        for(int i = left; i <= right; i++)
		        {
		            int x = dfs(left, i - 1);
		            int y = dfs(i + 1, right);
		
		            // ret 为当前区间能够获胜的最小现金数
		            // max(x, y) 为两个子树中最坏的情况需要支付的现金
		            ret = min(ret, max(x, y) + i);
		        }
		
		        memo[left][right] = ret;
		        return ret;
		    }
		};

5. 矩阵中的最长递增路径

题目链接 -> Leetcode -329.矩阵中的最长递增路径

Leetcode -329.矩阵中的最长递增路径

题目：给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度。

对于每个单元格，你可以往上，下，左，右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）。

示例 1：

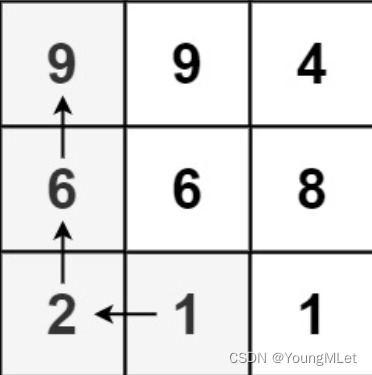
输入：matrix = [[9, 9, 4], [6, 6, 8], [2, 1, 1]]
输出：4
解释：最长递增路径为[1, 2, 6, 9]。

示例 2：

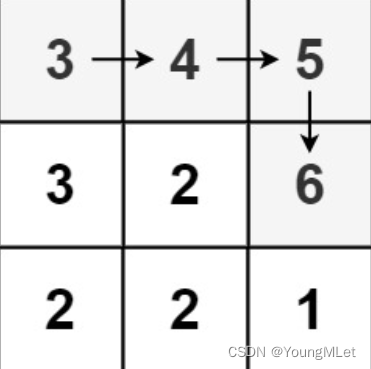
输入：matrix = [[3, 4, 5], [3, 2, 6], [2, 2, 1]]
输出：4
解释：最长递增路径是[3, 4, 5, 6]。注意不允许在对角线方向上移动。

示例 3：
输入：matrix = [[1]]
输出：1

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• 0 <= matrix[i][j] <= 2^31 - 1

思路：记忆化搜索：

• 加上一个"备忘录"；
• 每次进入递归的时候，去"备忘录"里面看看；
• 每次返回的时候，将结果加入到"备忘录"里面；

代码如下：

		class Solution 
		{
		    int dx[4] = {0, 0, 1, -1};
		    int dy[4] = {1, -1, 0, 0};
		    int m, n;
		    int memo[201][201];
		public:
		    // 记忆化搜索
		    int longestIncreasingPath(vector<vector<int>>& matrix) 
		    {
		        m = matrix.size(), n = matrix[0].size();
		        int ret = 1;
		
		        // 枚举从每个位置出发寻找最长递增路径
		        for(int i = 0; i < m; i++)
		        {
		            for(int j = 0; j < n; j++)
		            {
		                ret = max(ret, dfs(i, j, matrix));
		            }
		        }
		        return ret;
		    }
		
		    int dfs(int row, int col, vector<vector<int>>& matrix)
		    {
		        if(memo[row][col] != 0) return memo[row][col];
		
		        int ret = 1;
		        for(int k = 0; k < 4; k++)
		        {
		            int x = row + dx[k], y = col + dy[k];
		            if(x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[row][col])
		            {
		                // 保存当前位置的最长递增路径
		                ret = max(ret, dfs(x, y, matrix) + 1);
		            }
		        }
		        memo[row][col] = ret;
		        return ret;
		    }
		};