【数据结构】- 排序（详细介绍几种排序算法！！！*直接插入排序，*希尔排序，*选择排序，*堆排序，*冒泡排序，*快速排序，*归并排序）

排序无处不在，所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。

内部排序：数据元素全部放在内存中的排序。
外部排序：数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序。

今天介绍几种常见的排序算法：

直接插入排序

直接插入排序是一种稳定的内部排序算法，它适用于 小规模 数据或基本有序的数据集合，其核心思想是将待排序的元素逐个插入已排序序列中的适当位置，最终得到一个有序序列

在日常生活中，摸扑克牌就是运用到了直接插入排序。

直接插入排序过程如动画所示：

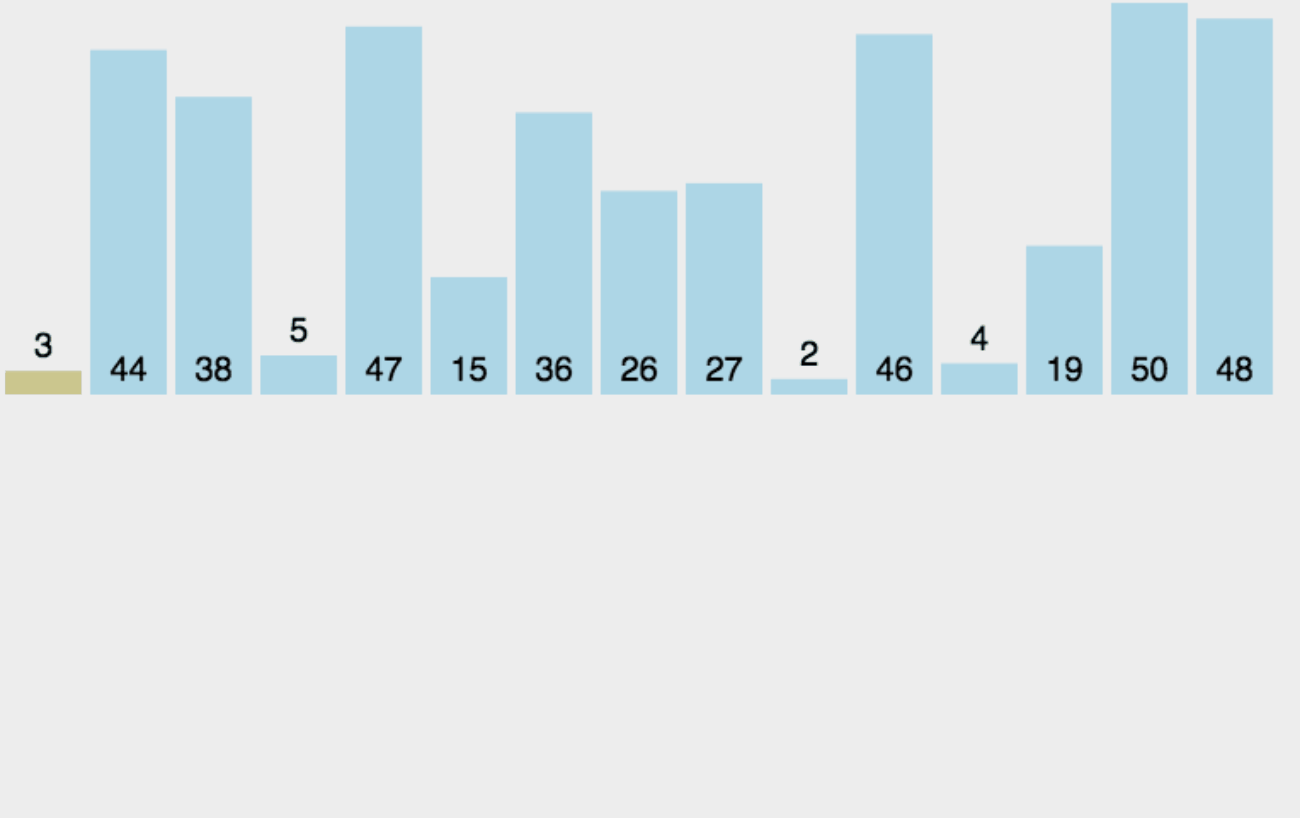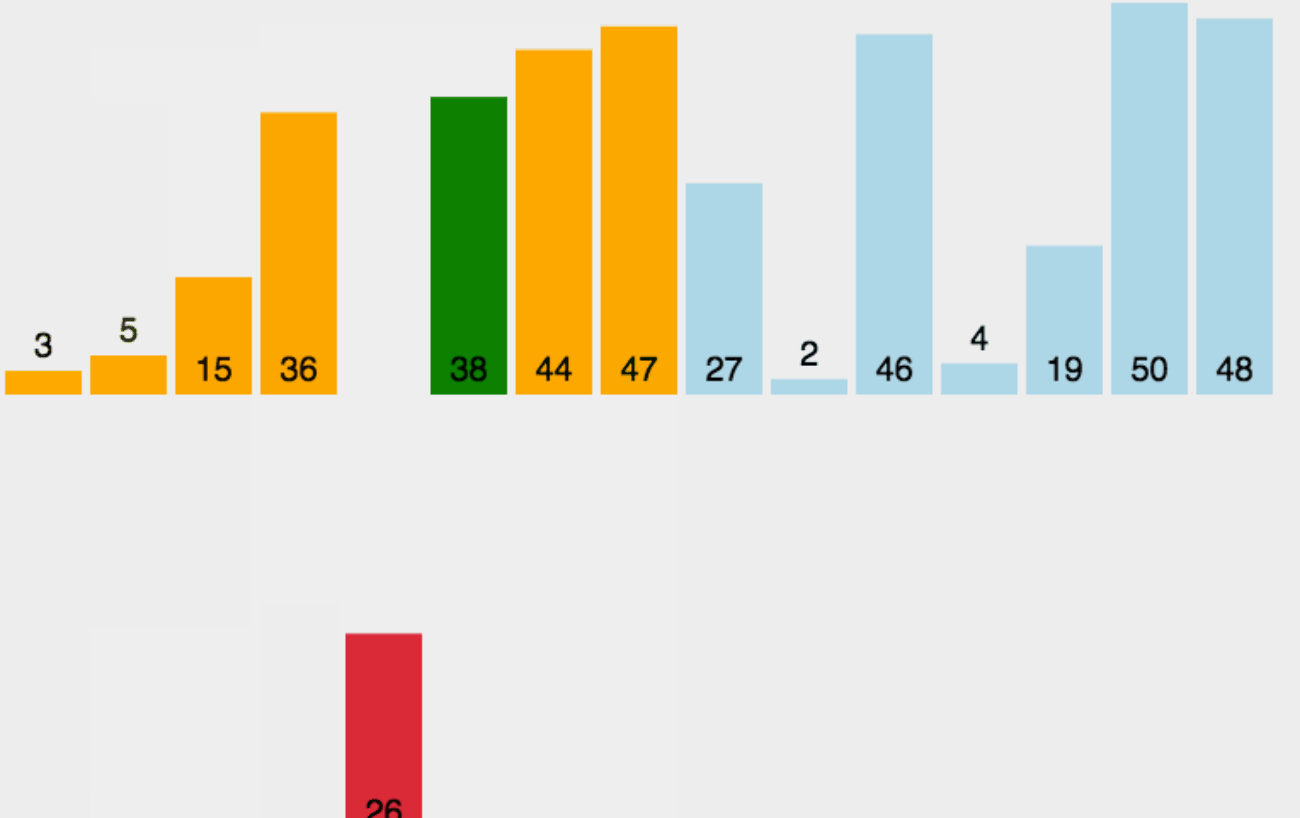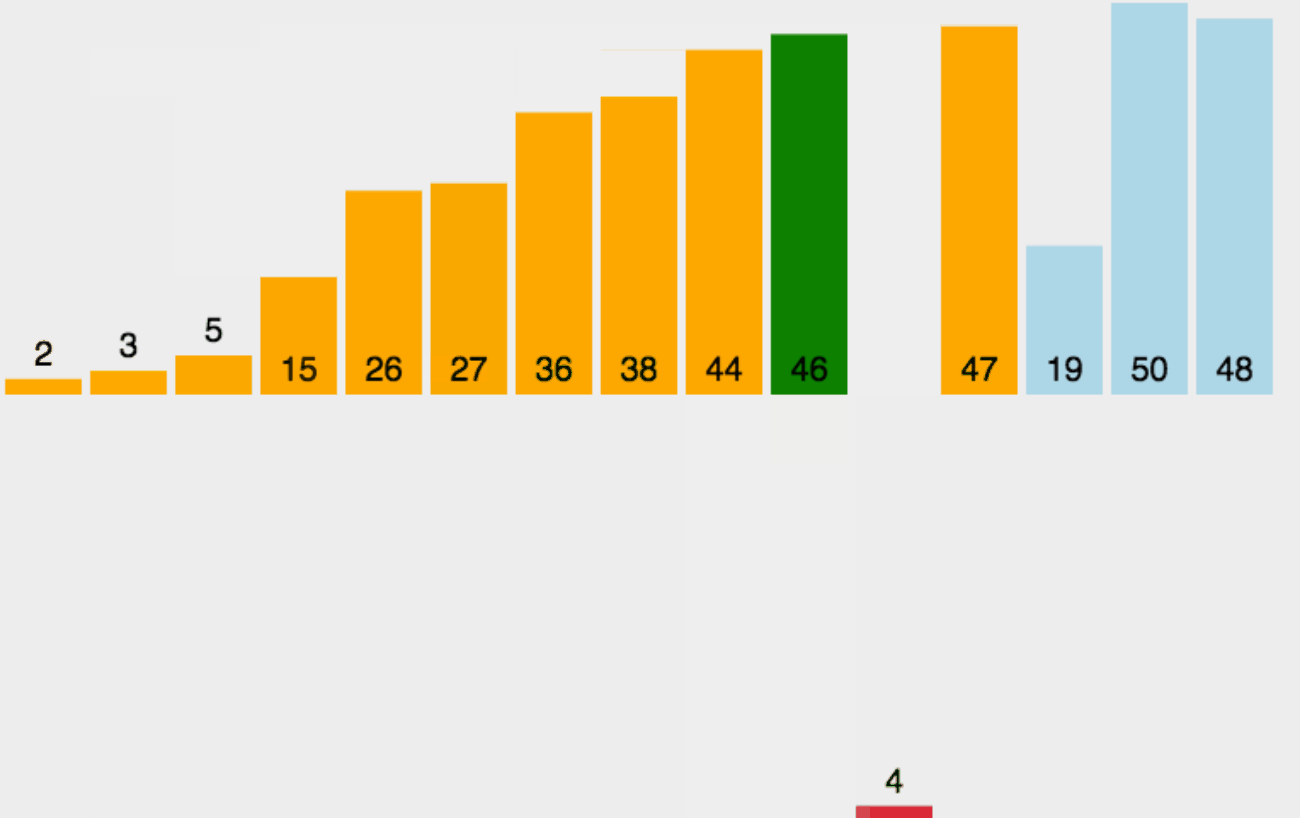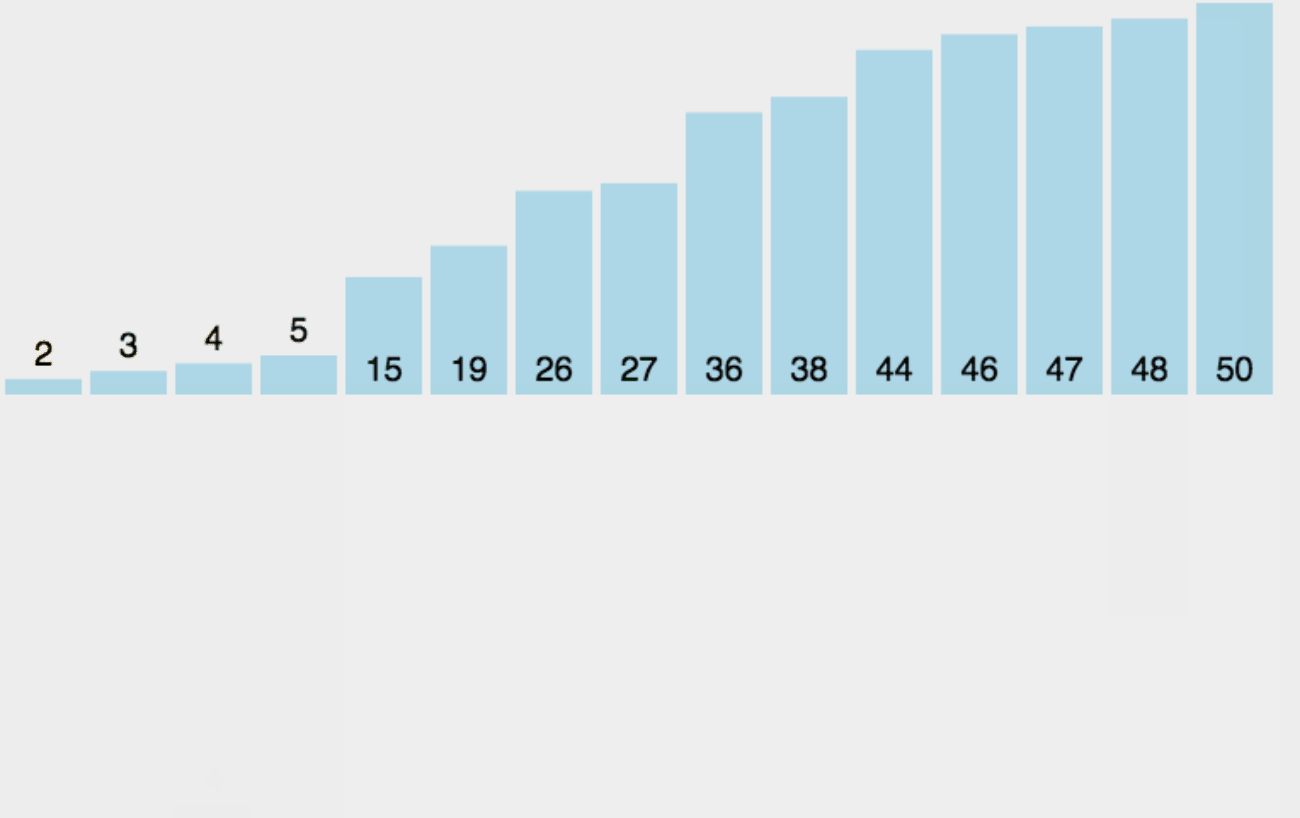
下面是直接插入排序的基本步骤：

• 1.首先，从第二个元素开始，将该元素视为已排序序列。
• 2.将当前元素与已排序序列进行比较，找到合适的插入位置。
• 3.将当前元素插入到已排序序列的适当位置，并将插入位置之后的元素依次后移。
• 4.重复步骤2和步骤3，直到所有元素都被插入到正确的位置。

代码演示：

#include <stdio.h>

void InsertSort(int arr[], int n) {
    int i, key, j;
    for (i = 1; i < n; i++) {
        key = arr[i];
        j = i - 1;
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j = j - 1;
        }
        arr[j + 1] = key;
    }
}

int main() {
    int arr[] = {5, 2, 8, 12, 3};
    int n = sizeof(arr) / sizeof(arr[0]);
    InsertSort(arr, n);
    
    printf("Sorted array: ");
    for (int i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    
    return 0;
}

这个代码中的 InsertSort 函数使用直接插入排序算法对输入的数组进行排序。在主函数中，我们定义了一个整数数组 arr，并使用 sizeof 操作符计算数组的大小。然后，我们调用 InsertSort 函数对数组进行排序，并打印排序后的结果。

运行上述代码，输出将会是 Sorted array: 2 3 5 8 12，表示数组已经按升序排列好了。

通过代码和直接插入排序的过程可知，直接插入排序的时间复杂度为O(n^2)，其中n是待排序序列的长度。在最坏情况下，即待排序序列为逆序时，需要进行n(n-1)/2次比较和移动操作。然而，在最好情况下，即待排序序列已经有序时，只需要进行n-1次比较且无需移动元素，时间复杂度为O(n)。

除了时间复杂度外，当待排序序列规模较大且无序时，直接插入排序的效率较低。
每次插入都需要移动大量元素，耗费时间。

尽管直接插入排序在某些方面存在一些限制，但它作为一种简单而有效的排序算法，在实际应用中仍然有其价值。特别是在处理小规模数据或基本有序的数据集合时，直接插入排序可以提供较好的性能。

总而言之，直接插入排序是一种常用的排序算法，通过将待排序元素逐个插入已排序序列中的适当位置，实现对整个序列的排序。虽然它的时间复杂度较高，但在某些情况下仍然具有一定的优势。对于初学者来说，直接插入排序是一个很好的入门算法，有助于理解和掌握排序算法的基本思想。

希尔排序

介绍完直接插入排序，再说一说希尔排序（Shell Sort），希尔排序是一种高效的排序算法，它是直接插入排序的改进版本，通过引入分组和逐步缩小间隔的方式，可以以更快的速度对大规模数据进行排序。

希尔排序的步骤为：

• 确定一个间距（gap）值，通常是将数组长度除以2，然后不断除以2，直到gap值为1

• 根据当前的gap值，将待排序数组分成若干个子序列。每个子序列相隔gap个位置，即第一个子序列包含第0、第gap、第2gap…位置上的元素，第二个子序列包含第1、第1+gap、第1+2gap…位置上的元素，依此类推。
  

• 对每个子序列进行排序。

• 缩小gap值并重复步骤2和3，在步骤3完成后，将gap减小（通常是除以2），再次进行步骤2和步骤3。不断缩小gap并重复步骤2和3，直到gap值为1时，进行最后一次排序。

动画演示整体过程（动图中d表示的就是gap值）

代码演示希尔排序：

#include <stdio.h>

void hellSort(int arr[], int n) {
    int gap, i, j, temp;
    
    for (gap = n / 2; gap > 0; gap /= 2) {
        for (i = gap; i < n; i++) {
            temp = arr[i];
            
            for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {
                arr[j] = arr[j - gap];
            }
            
            arr[j] = temp;
        }
    }
}

int main() {
    int arr[] = {5, 2, 8, 12, 3};
    int n = sizeof(arr) / sizeof(arr[0]);
    
    ShellSort(arr, n);
    
    printf("Sorted array: ");
    for (int i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    
    return 0;
}

最后输出运行结果Sorted array: 2 3 5 8 12，成功将数组 [5, 2, 8, 12, 3] 进行希尔排序，并输出排序后的结果。数组被排序成升序序列 [2, 3, 5, 8, 12]。

总的来说：希尔排序通过逐步缩小gap值的方式，先对数组中相距较远的元素进行排序，使得整个数组的某些部分变得基本有序，然后逐渐减小gap值，直至为1，完成最后一次排序。

希尔排序的时间复杂度是比较复杂的，它取决于增量序列的选择。希尔排序的最坏时间复杂度是 O(n^2)，但在平均情况下，它的时间复杂度通常为 O(n log n)。希尔排序的时间复杂度分析较为复杂，目前还没有找到一个确定的最佳增量序列。因此，在实际应用中，对于不同的问题规模和数据特点，需要根据实际情况选择合适的增量序列，以达到更好的排序性能。

?希尔排序这种分组和逐步缩小间隔的策略可以提高插入排序的效率，使得希尔排序在处理大规模数据时更加高效。

选择排序

选择排序是一种简单直观的排序算法，它的思想很容易理解并且易于实现。选择排序的基本思想是在待排序数组中找到最小（或最大）元素，将其放到数组的起始位置，然后从剩余未排序的元素中再找到最小（或最大）元素，放到已排序部分的末尾。以此类推，直到整个数组排序完成。

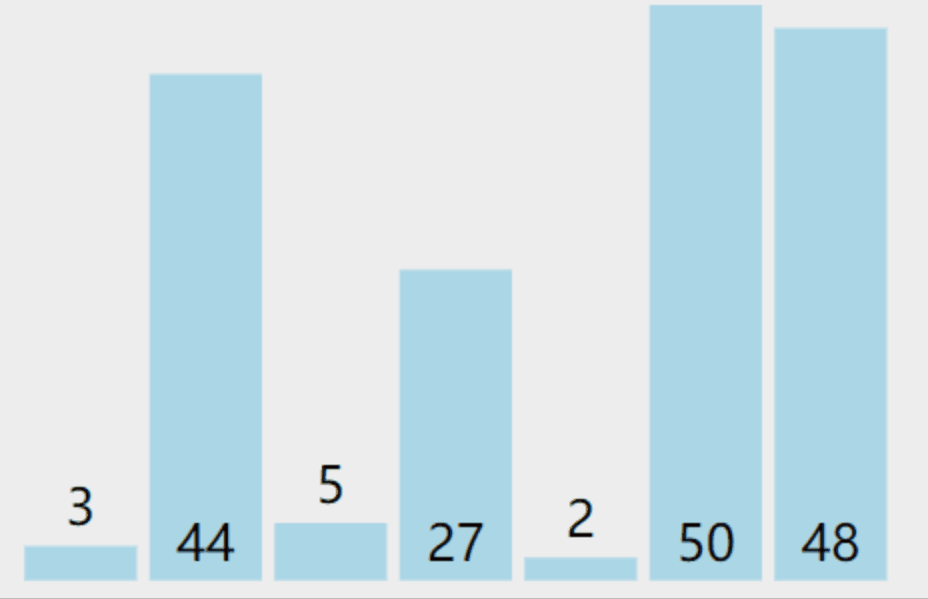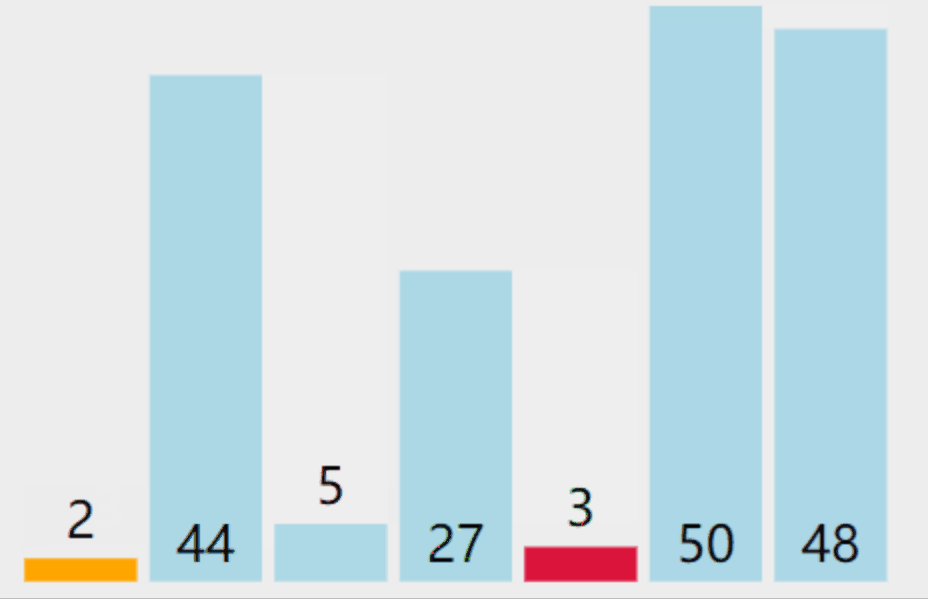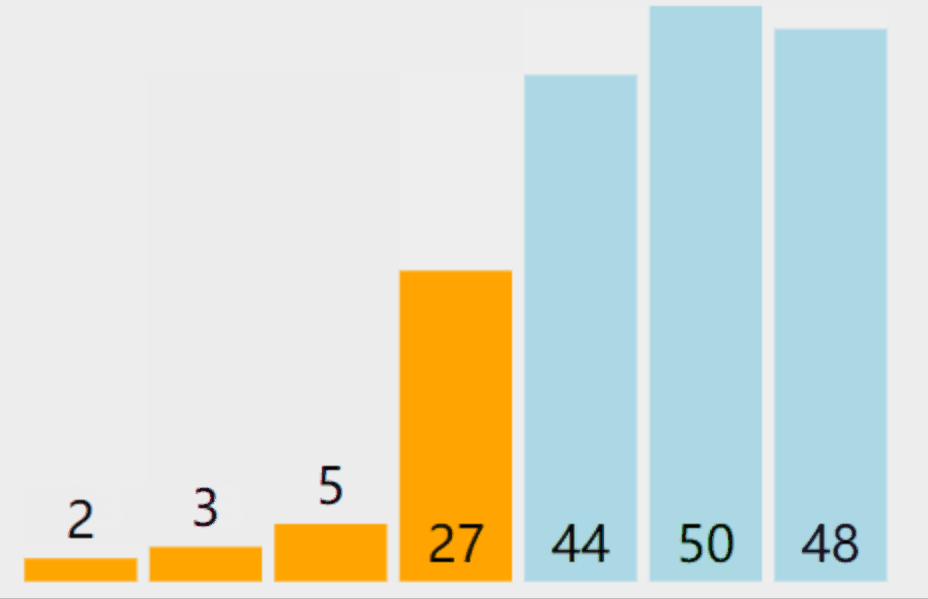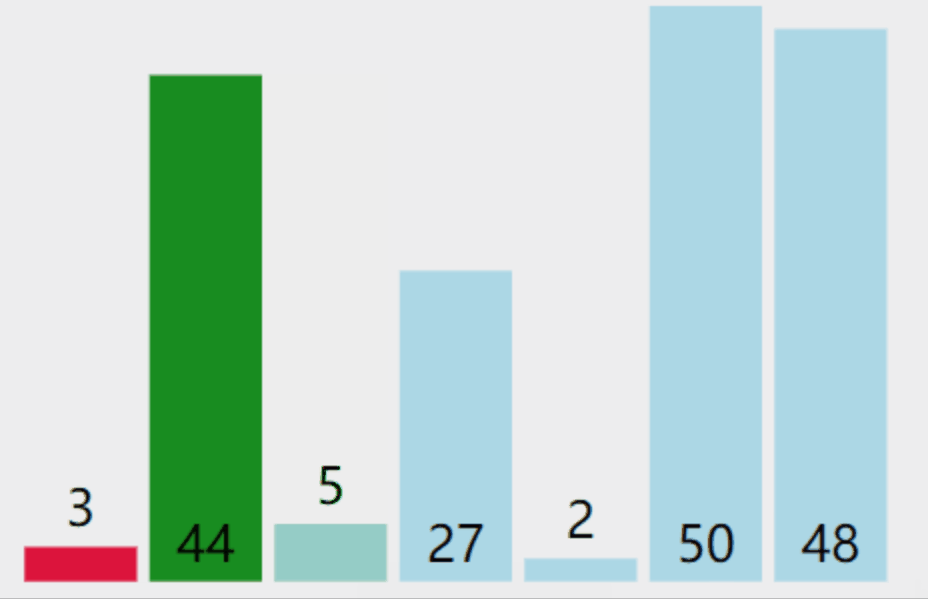
下面详细介绍选择排序基本步骤：

• 从数组中选择最小的元素，将其与数组的第一个元素交换位置。
• 从剩余的未排序元素中选择最小的元素，将其与数组的第二个元素交换位置。
• 重复上述步骤，每次在剩余未排序的元素中选择最小（或最大）的元素，然后将其与当前位置对应的元素交换位置。每一次遍历都能确定一个位置上的元素。
• 重复进行遍历直到所有元素都被放置在正确的位置上。这样整个数组就完成了排序

进行排序的过程中需要注意的是，在每次遍历中，选择排序只进行一次交换操作，即将最小（或最大）的元素放到正确的位置上。因此，选择排序的交换次数相对较少，适用于对于交换操作比较耗时的情况。

下面是使用 C 语言实现的选择排序：

#include <stdio.h>

void swap(int* a, int* b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

void SelectionSort(int arr[], int n) {
    for (int i = 0; i < n - 1; i++) {
        int minIndex = i;
        
        for (int j = i + 1; j < n; j++) {
            if (arr[j] < arr[minIndex]) {
                minIndex = j;
            }
        }
        
        swap(&arr[i], &arr[minIndex]);
    }
}

int main() {
    int arr[] = {5, 2, 8, 12, 3};
    int n = sizeof(arr) / sizeof(arr[0]);
    
    SelectionSort(arr, n);
    
    printf("Sorted array: ");
    for (int i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    
    return 0;
}

代码最后的输出结果为Sorted array: 2 3 5 8 12

选择排序的时间复杂度为 O(n^2)，其中 n 是待排序数组的大小。虽然它不是最优的排序算法，但对于小规模的数据排序来说，它仍然是一个简单且有效的选择。

堆排序

堆排序我认为应该和二叉树结合在一起才对，等赶出二叉树的博客，此处会传送到二叉树…

冒泡排序

冒泡排序作为一种简单但低效的排序算法，常常被用于教学和入门级应用。

冒泡排序是比较简单的排序，这里话不多说直接介绍冒泡排序的步骤：

• 从数组的第一个元素开始，依次比较相邻的两个元素。如果前一个元素比后一个元素大，则交换它们的位置。
• 重复上述步骤，直到没有任何一对相邻元素需要交换位置为止。每次操作会把最大的元素“冒泡”到最后一个未排序的位置。
  
  代码演示：

#include <stdio.h>

// 交换两个元素的位置
void swap(int* a, int* b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

// 冒泡排序函数
void bubbleSort(int arr[], int n) {
    for (int i = 0; i < n - 1; i++) {
        // 在每轮操作中，从第一个元素开始比较相邻的两个元素
        for (int j = 0; j < n - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                swap(&arr[j], &arr[j + 1]);
            }
        }
    }
}

int main() {
    int arr[] = {5, 2, 8, 12, 3};
    int n = sizeof(arr) / sizeof(arr[0]);

    bubbleSort(arr, n);

    printf("Sorted array: ");
    for (int i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }

    return 0;
}

在上述代码中，我们首先实现了一个swap函数用于交换数组中两个元素的位置。然后，在bubbleSort函数中，我们通过两层循环来实现冒泡排序算法。每轮操作会将当前未排序部分中最大的元素“冒泡”到最后。当没有任何一对相邻元素需要交换位置时，排序完成。

冒泡排序的特点：

时间复杂度：冒泡排序的时间复杂度为O(n^2)，其中n是待排序数组的长度。由于需要进行多次比较和交换操作，所以冒泡排序在处理大规模数据时效率较低。
原地排序：冒泡排序是一种原地排序算法，不需要额外的空间。
稳定性：由于冒泡排序中只有相邻元素之间的比较和交换，所以它是一种稳定的排序算法。
适用性：冒泡排序在处理小规模数据时表现出色，但在处理大规模数据时效率较低。因此，它通常被用于教学和入门级应用，而在生产环境中很少使用

尽管冒泡排序算法简单易懂，但其时间复杂度较高，效率较低，因此在实际应用中不太常用。

快速排序

快速排序（Quick Sort）是一种高效的排序算法，它采用了“分治”的思想，通过递归地将问题划分为更小的子问题来解决。相较于其他排序算法，快速排序具有较快的平均时间复杂度和较小的空间复杂度。

快速排序的步骤为：

• 选择一个基准元素（通常选择数组的第一个元素）。
• 将小于等于基准元素的数放在其左侧，大于基准元素的数放在其右侧。
• 对左右两个子数组递归地重复上述步骤，直到子数组的大小为 1 或 0。

用代码实现：

#include <stdio.h>

// 交换数组中两个元素的值
void swap(int* a, int* b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

// 快速排序函数
void quickSort(int arr[], int left, int right) {
    if (left < right) {
        int pivot = arr[left];  // 基准元素
        int i = left, j = right;
        
        while (i < j) {
            // 从右向左找到第一个小于基准元素的数
            while (i < j && arr[j] >= pivot) {
                j--;
            }
            if (i < j) {
                swap(&arr[i], &arr[j]);
                i++;
            }
            
            // 从左向右找到第一个大于基准元素的数
            while (i < j && arr[i] < pivot) {
                i++;
            }
            if (i < j) {
                swap(&arr[i], &arr[j]);
                j--;
            }
        }
        
        // 将基准元素放到最终位置
        arr[i] = pivot;
        
        // 递归地对左右子数组进行排序
        quickSort(arr, left, i - 1);
        quickSort(arr, i + 1, right);
    }
}

// 测试代码
int main() {
    int arr[] = {5, 2, 8, 12, 3};
    int size = sizeof(arr) / sizeof(arr[0]);
    
    quickSort(arr, 0, size - 1);
    
    printf("排序结果：");
    for (int i = 0; i < size; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
    
    return 0;
}

在上面的代码中，我们定义了一个 swap 函数来交换两个元素的值。然后，我们实现了 quickSort 函数来执行快速排序算法。在该函数中，我们选择数组的第一个元素作为基准元素，并使用双指针法将小于等于基准元素的数放在其左侧，大于基准元素的数放在其右侧。最后，我们递归地对左右子数组进行排序。

运行代码后输出：排序结果：2 3 5 8 12 完成排序

在我看来，快速排序是最优的一种排序，它的时间、空间复杂度低。应用广泛。
快速排序的时间复杂度为 O(nlogn)，相比于其他排序算法如冒泡排序和插入排序，它在大规模数据处理上有更快的表现。快速排序只需要一个元素的额外空间来存储递归时的基准元素，因此其空间复杂度为 O(1)。所以可以进行原地排序，即不需要额外的辅助空间，这对于空间有限的场景非常适用。

归并排序

归并排序（Merge Sort）也是一种基于分治思想的排序算法，其主要思路是将待排序数组分成两个子数组，递归地对子数组进行排序，然后将已排序的子数组合并成一个有序数组。相较于其他排序算法，归并排序具有时间复杂度稳定、空间复杂度较低的优点。

归并排序的基本步骤如下：

• 将待排序数组分成两个子数组，每个子数组包含大约一半的元素。
• 递归地对每个子数组进行排序，直到子数组的长度为 1。
• 合并已排序的子数组，产生一个新的已排序的数组。
  

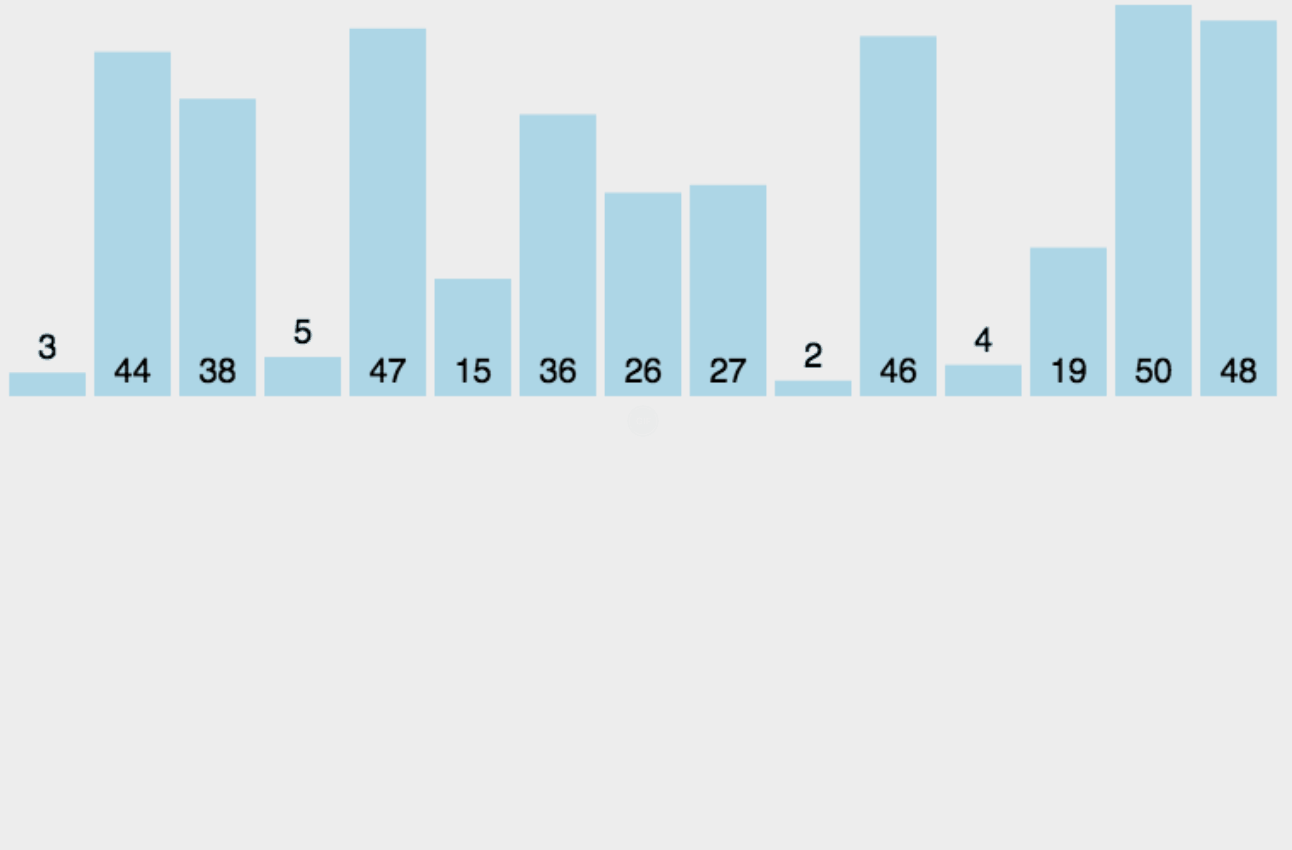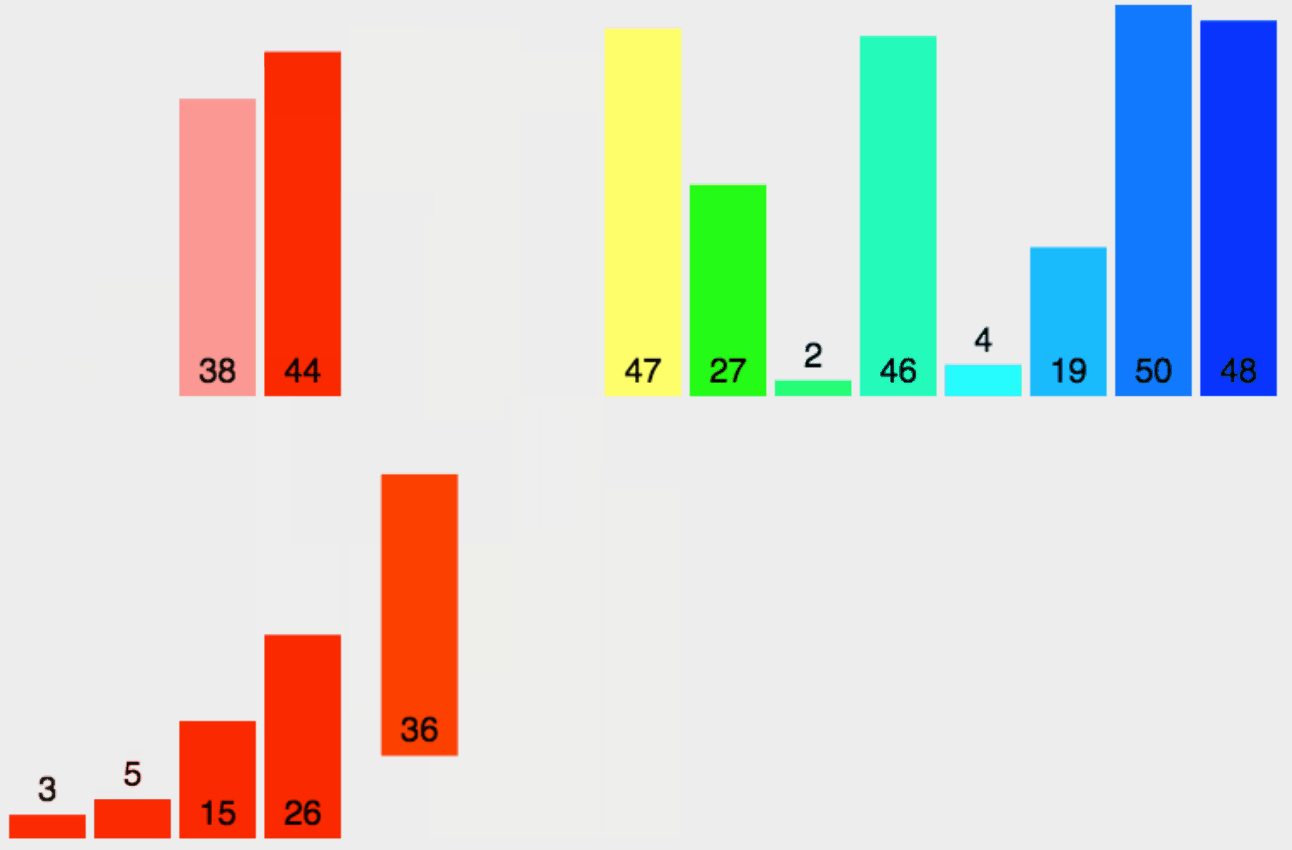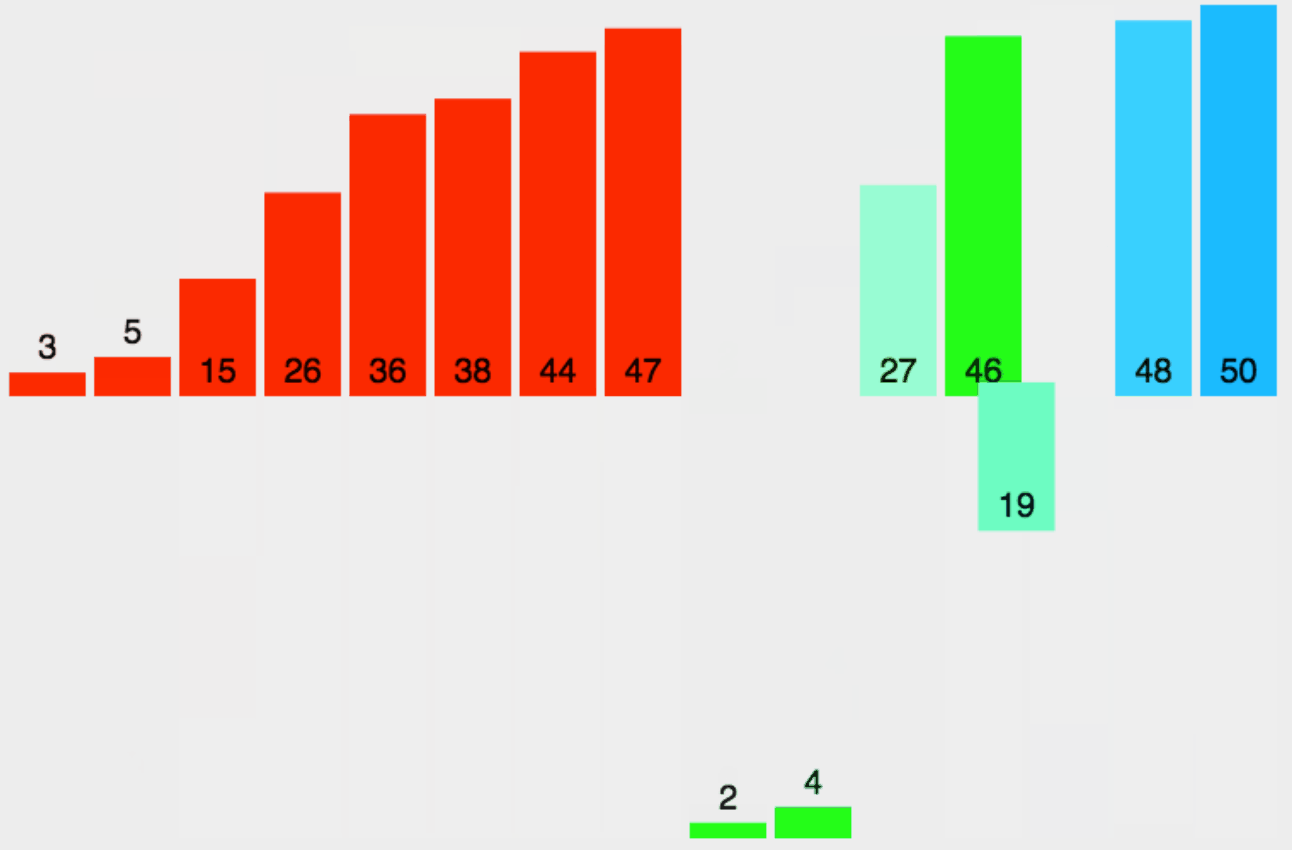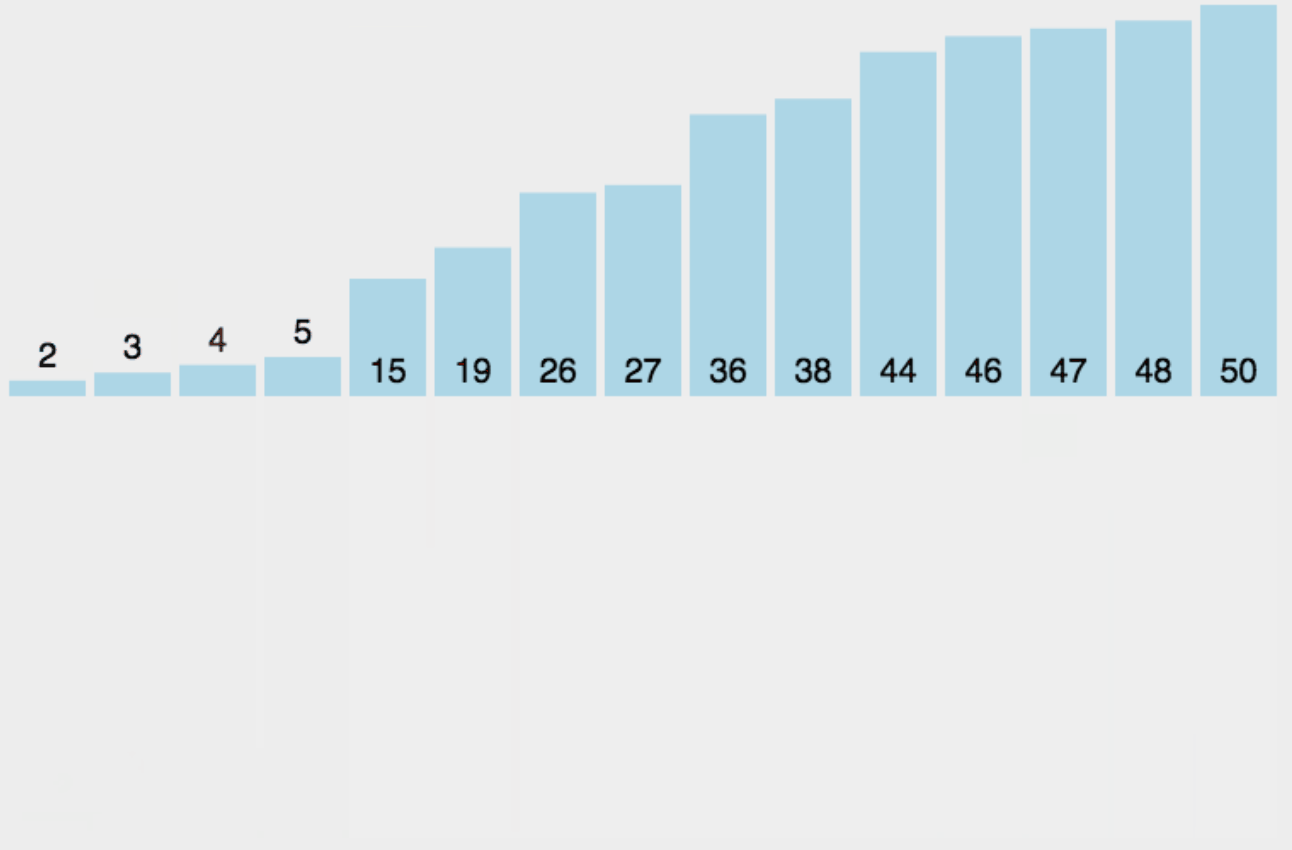
在合并已排序的子数组时，需要比较两个子数组中的元素，并将它们按升序或降序插入到新数组中。具体实现中通常使用一个额外的辅助数组来存储归并过程中的结果。
用代码实现其过程：

#include <stdio.h>
#include <stdlib.h>

// 合并两个已排序的子数组
void merge(int arr[], int left, int mid, int right) {
    int i, j, k;
    int n1 = mid - left + 1;
    int n2 = right - mid;
    
    // 创建临时数组
    int* L = (int*) malloc(n1 * sizeof(int));
    int* R = (int*) malloc(n2 * sizeof(int));
    
    // 将数据拷贝到临时数组中
    for (i = 0; i < n1; i++) {
        L[i] = arr[left + i];
    }
    for (j = 0; j < n2; j++) {
        R[j] = arr[mid + 1 + j];
    }
    
    // 合并两个已排序的子数组
    i = 0;
    j = 0;
    k = left;
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k++] = L[i++];
        }
        else {
            arr[k++] = R[j++];
        }
    }
    
    // 将剩余的元素拷贝到数组中
    while (i < n1) {
        arr[k++] = L[i++];
    }
    while (j < n2) {
        arr[k++] = R[j++];
    }
    
    // 释放临时数组
    free(L);
    free(R);
}

// 归并排序函数
void mergeSort(int arr[], int left, int right) {
    if (left < right) {
        int mid = left + (right - left) / 2;  // 中间位置
        
        // 对左右两个子数组递归地进行排序
        mergeSort(arr, left, mid);
        mergeSort(arr, mid + 1, right);
        
        // 合并两个已排序的子数组
        merge(arr, left, mid, right);
    }
}

// 测试代码
int main() {
    int arr[] = {5, 2, 8, 12, 3};
    int size = sizeof(arr) / sizeof(arr[0]);
    
    mergeSort(arr, 0, size - 1);
    
    printf("排序结果：");
    for (int i = 0; i < size; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
    
    return 0;
}

在上面的代码中，我们定义了一个 merge 函数来合并两个已排序的子数组。然后，我们实现了 mergeSort 函数来执行归并排序算法。在该函数中，我们使用递归将待排序数组分成两个子数组，并对每个子数组进行排序，然后调用 merge 函数将已排序的子数组合并成一个有序数组

运行代码输出结果：排序结果：2 3 5 8 12 完成排序。

归并排序是一种稳定的排序算法，时间复杂度为 O(n log n)，空间复杂度为 O(n)。它的时间复杂度相对稳定，不会因为数据分布的情况而波动，因此在实际应用中也得到了广泛的使用。