场景识别与词袋模型

---

---

1. 任务要求

• 输入：给定测试集图片，预测在15个场景中的类别。
• 任务：
  • 实现Tiny images representation。
  • 实现最近邻分类器nearest neighbor classifier。
  • 实现SIFT特征词袋表示
• 输出：
  • 针对Tiny images representation 和SIFT 词袋表示，报告每个类别的准确度和平均准确度。
  • 对这两种方案，对正确和错误的识别结果挑出示例进行可视化。
  • 探索不同的参数设置对结果的影响，总结成表格。
  • 通过实验讨论词汇量的大小对识别分类结果的影响，比如哪个类别的识别准确率最高/最低，原因是什么。

---

2. 数据集

http://www.cad.zju.edu.cn/home/gfzhang/course/cv/Homework3.zip

---

3. 实现算法

3.1 目标实现

本报告的主题是图像识别，旨在实现输入多个具有label的不同场景的图片，通过Tiny images representation或者特征词袋表示结合最近邻分类器预测给定测试集图片的类别结果以及分类准确率。

本报告主要实现了以下目标：

• 使用Tiny images representation和SIFT或HOG特征词袋对图像进行特征提取和描述。
• 实现了最近邻分类器nearest neighbor classifier和支持向量机support vector machine，并结合提取到的图像特征进行分类。
• 可视化展示15个场景分类准确率的混淆矩阵。
• 通过调整图像特征提取的关键参数，比如小图像特征尺寸和特征词汇量大小等探索不同的参数设置对结果的影响。
• 展示不同图像特征提取方法以及不同分类器的部分样本结果。

3.2 Tiny images representation

Tiny Images Representation（微图像表示）是一种基于图像特征的图像表示方法。它是由Alex Krizhevsky于2009年提出的，旨在通过利用大规模图像数据集的统计信息来表示图像。其主要思想是将每个图像转换为一个固定长度的向量，以便在机器学习任务中使用。这里的转换过程包括以下几个步骤：

• 预处理：首先，将图像调整为统一的大小（默认为16×16px）。
• 特征提取：对于每个调整后的图像，将其转换为一个固定长度的特征向量。我们使用的方法是将图像的像素值展平为一维数组，并对像素值进行归一化处理，以确保特征向量具有相似的尺度。

通过这样的转换过程，每个图像都被表示为一个固定长度的特征向量，其中每个维度对应于图像中的一个像素位置。Tiny Images Representation 的优点是简单且易于计算，同时可以捕捉到大规模图像数据集的统计特征。

3.3 SIFT特征词袋表示

SIFT（Scale-Invariant Feature Transform，尺度不变特征变换）是一种用于图像特征提取的算法。SIFT算法最初由David Lowe于1999年提出，它对图像中的局部特征进行检测和描述，具有尺度不变性和旋转不变性等优点。SIFT特征词袋表示是基于SIFT特征的一种向量表示方法，常用于图像分类和目标识别任务。SIFT特征词袋表示的主要步骤如下：

• 特征提取：使用SIFT算法检测图像中的关键点（keypoints）并计算每个关键点的描述子（descriptor）。SIFT算法通过在不同尺度空间上的高斯差分图像中寻找局部极值点来检测关键点，然后利用关键点周围的图像梯度信息生成描述子。
• 特征量化：将SIFT描述子量化为固定长度的向量。我们使用聚类算法（Mini Batch K-means）对描述子进行聚类，得到一组聚类中心（视觉词汇）。每个描述子被分配到最近的聚类中心，形成一个词袋（bag-of-words）表示。
• 生成特征向量：对于测试集的图像，同样使用SIFT算法检测图像中的关键点并计算其描述子。对于每个图像，统计其词袋中每个聚类中心的出现频率，形成一个特征向量。该特征向量被视为图像的特征表示，反映了图像中不同视觉词汇的分布情况，作为图像特征输入分类器可以对测试数据进行分类。

3.4 相关算法

报告中使用的其他相关算法如HOG、NNS和SVM等这里不做过多详细介绍。

---

4. 实验结果

4.1 基础结果展示

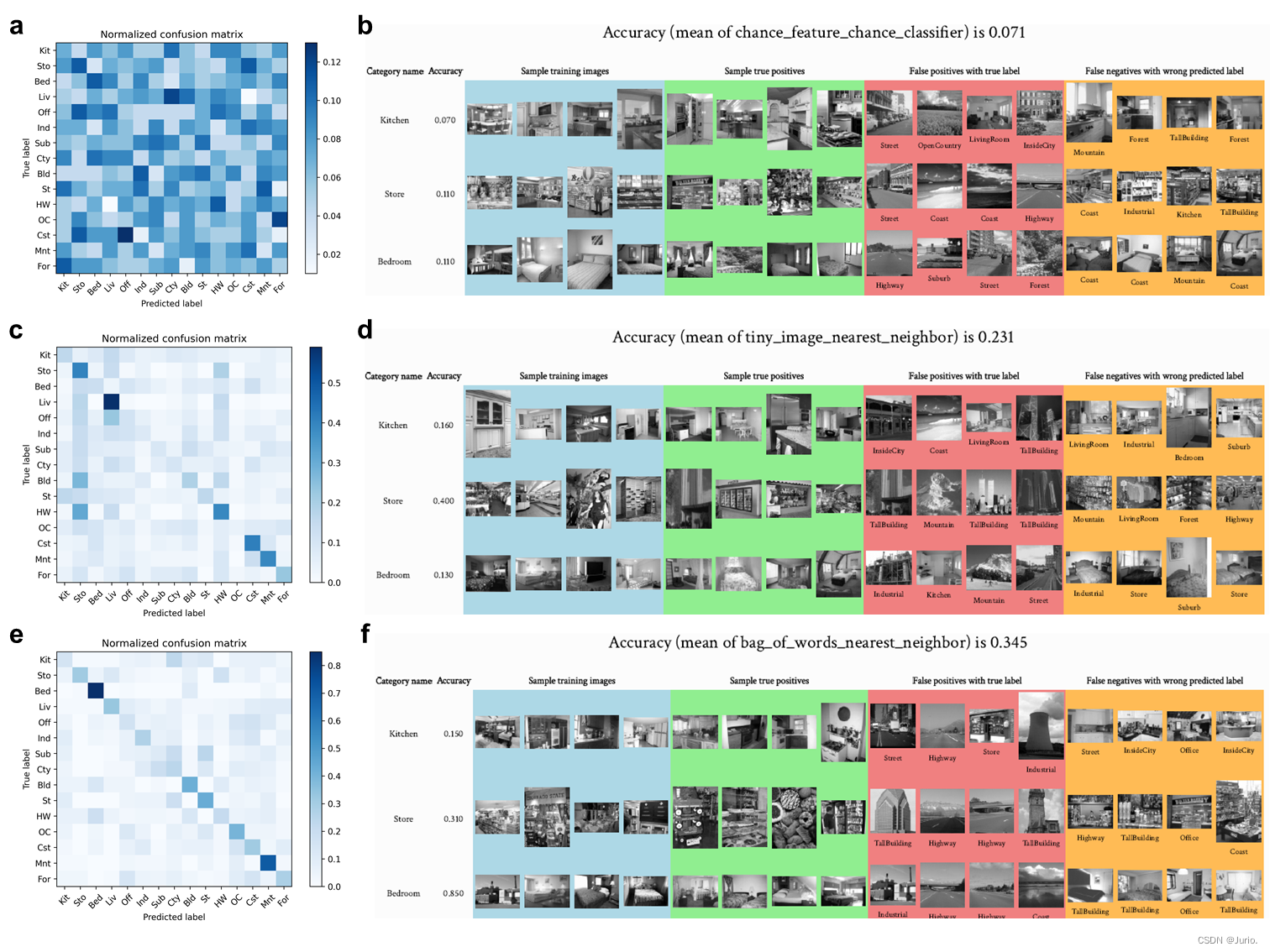
Figure 1展示了三种路径得到的分类精度混淆矩阵和部分样本结果。图a为不使用任何图像特征和随机分类得到的混淆矩阵，随机性能为0.071，混淆矩阵横轴为预测类别，纵轴为真实类别。b图截取了15个场景中3个类别的部分样本，左侧两列分别为类别和当前类别的分类精度，Sample training images（蓝色）为训练集中的正样本，Sample true positives（绿色）为测试集中分类正确的正样本，False positives withtrue label（红色）为测试集中当前分类器分类错误但其真实类别对应的分类器分类正确的负样本（即当前分类器的负样本和目标类别分类器的正样本的交集），False negatives with wrong predicted label（黄色）为测试集中当前分类器分类错误且其真实类别对应的分类器分类错误的负样本（即当前分类器的负样本和目标类别分类器的负样本的交集）。c-d图对应Tiny images representation和最近邻分类器的分类结果（$Acc=0.231$），其中小图像特征大小为默认的16×16px。e-f图对应SIFT特征词袋表示和最近邻分类器的分类结果（$Acc=0.345$），其中SIFT特征词袋表示的词汇量大小为50。

Figure 1: 分类精度混淆矩阵和部分样本结果

4.2 算法超参的影响

4.2.1 Tiny images size

Tabel 1展示了不同小图像尺寸下最终15个类别的平均分类准确率。小图像尺寸对分类精度可能存在的影响：

• 信息损失：缩小图像尺寸会导致图像中的细节和纹理信息的丢失。较小的图像可能无法保留原始图像中的重要特征，从而可能降低分类的准确性。比如最小的4 × 4尺寸的分类精度最低。
• 特征冗余：当图像被缩小为较大尺寸时，可能会出现多个原始像素值映射到相同的小图像像素值的情况。这可能导致特征的冗余性增加，使得分类器难以区分不同类别之间的细微差别。比如当尺寸超过16 × 16时，分类精度开始下降，且随着尺寸越大精度越低。
• 计算效率提升：小图像尺寸可以降低特征的维度，减少模型训练和推理的计算复杂度，加快处理速度。所以需要保证分类精度的情况下，图像越小处理速度越快，在本实验中小图像尺寸为16 × 16最合适。

4.2.2 Vocabulary size

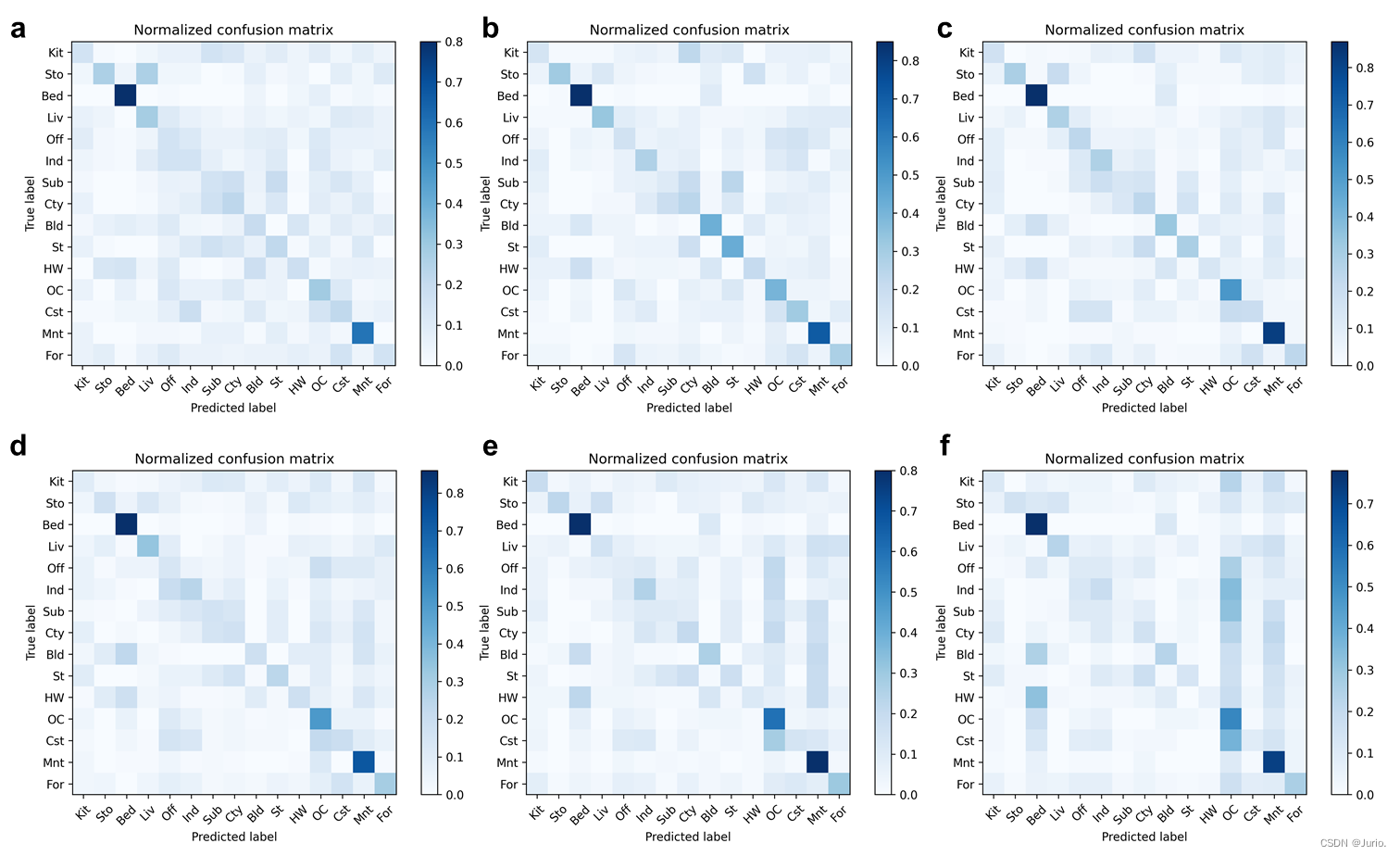
Figure 2为不同Vocabulary size的分类性能混淆矩阵，Tabel 2 为不同词带提取算法以及不同Vocabulary size的平均分类性能。Vocabulary size对分类精度可以产生一定的影响，具体效果取决于任务、数据集和算法的特点。词汇表大小对整体分类精度可能存在的影响：

• 信息丰富度：较大的词汇表大小可以提供更多的视觉词汇来捕捉图像的细节和纹理信息。这可以增加特征的丰富性，使分类器能够更好地区分不同的类别。因此，较大的词汇表大小通常有助于提高分类精度。比如Tabel 2中SIFT和HOG算法均在较大的词汇量50和200时性能比小词汇量更高。
• 过拟合：在某些情况下，较大的词汇表大小可能导致过拟合问题。如果词汇表过大，每个图像的特征向量维度也会增加，这可能导致训练样本不足的情况下出现过度拟合，从而降低分类器的泛化能力。因此，在有限的训练数据集上，过大的词汇表大小可能会导致分类精度下降。比如Tabel 2中SIFT和HOG算法在词汇量大于50和200时出现过拟合，分类精度下降。
• 复杂度：较大的词汇表大小会增加特征向量的维度，从而增加分类器的计算复杂度。在训练和推理阶段，需要处理更多的特征维度，可能需要更多的计算资源和时间。因此，较大的词汇表大小可能会增加系统的开销。在实验中记录下的提取特征运行时间随词汇量增大显著提高。

同时，词汇表大小对某些类别的分类精度影响也十分显著。从Figure 2可以看到，类别Mnt（“Mountain”）和OC（OpenCountry）随词汇量增大时分类精度逐渐提高，特别地在词汇量为400达到最高的0.800和0.600，这可能是由于较大的词汇表大小可以提供更多的视觉词汇用于描述细粒度类别的特征，从而提高“Mountain”这类特征密集的开阔场景分类的准确性。而特征较稀疏的类别如Liv（“LivingRoom”）、Bld（“TallBuilding”）、St（“Street”）等场景类别的分类精度在较小的词汇量如50左右的时候达到最高0.330、0.420和0.430，而这些场景在400词汇量时分类精度为0.150、0.260和0.170。

Figure 2: 不同Vocabulary size的分类性能混淆矩阵. a, 15. b, 50. c, 100. d, 200. e, 400. f, 800.

4.3 其他结果

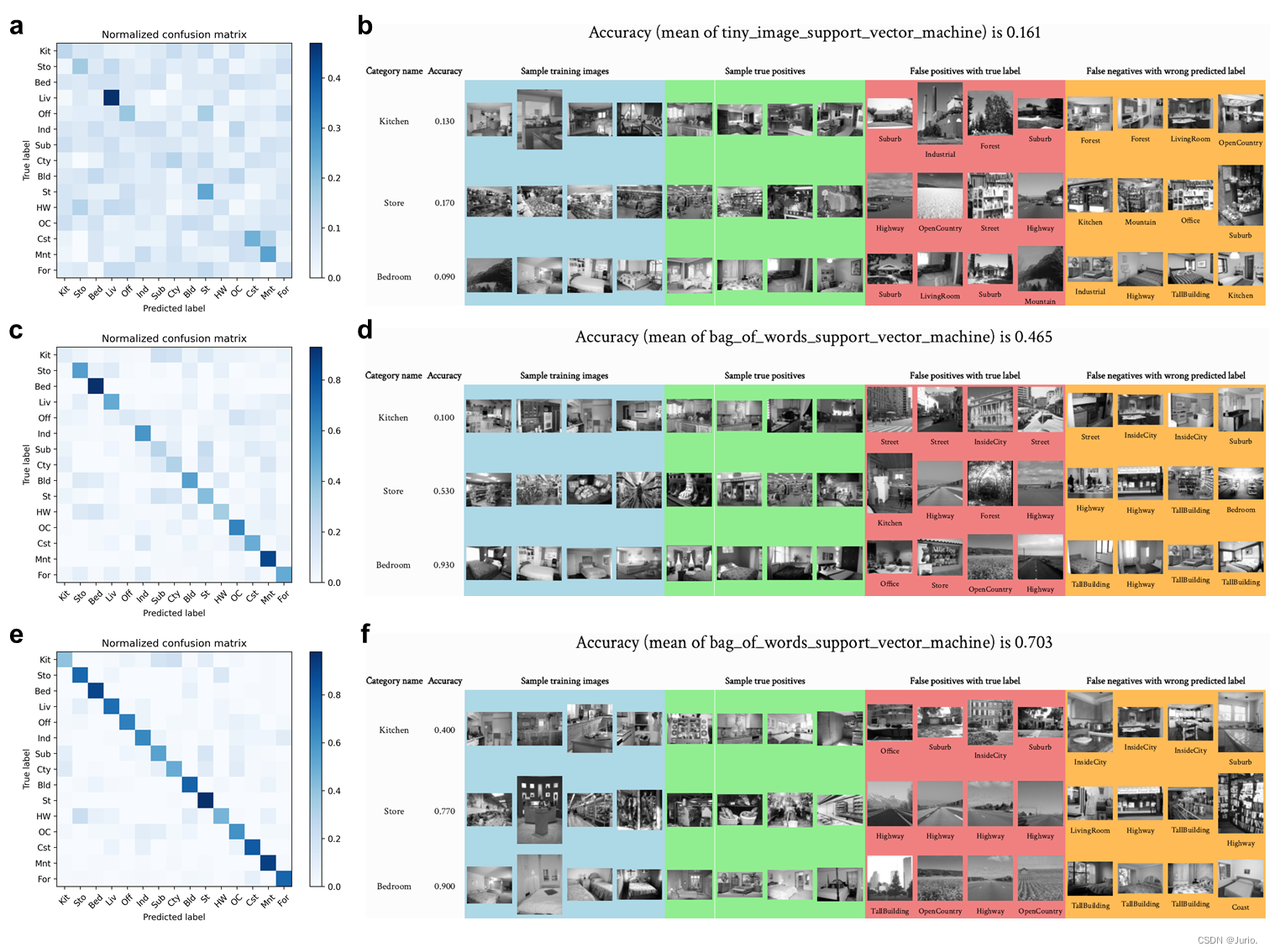
基于SVM分类器的部分结果可视化见Fig. S1。HOG_SVM的所有15类样本结果见Fig. S2。

Fig. S1. SVM的分类精度混淆矩阵和部分样本结果. a-b, Tiny Images Representation（16 × 16）. c-d, SIFT（50）. e-f, HOG（200）.

Fig. S2. HOG_SVM的15类样本结果.

---

5. 源代码

持续更新…

---

创作不易，麻烦点点赞和关注咯！