算法学习系列（二十三）：最小生成树问题

引言

这个最小生成树问题其实思想都非常的简单，然后代码也是比较简单的，很多人听到这个问题觉得难，比如说跟我一样，主要是因为不知道这个算法，就是一种未知的恐惧，所以在心里就觉得很难并且产生抗拒心理，但只要你慢慢尝试了解之后，才会发现这个问题其实比之前介绍的算法都还要简单，所以说还是要以行动来打破焦虑，才是最根本最快的方法，话不多说，那就开始吧。

一、最小生成树问题

这个最小生成树主要是用来解决，一个图中经过所有点的最短距离是多少。
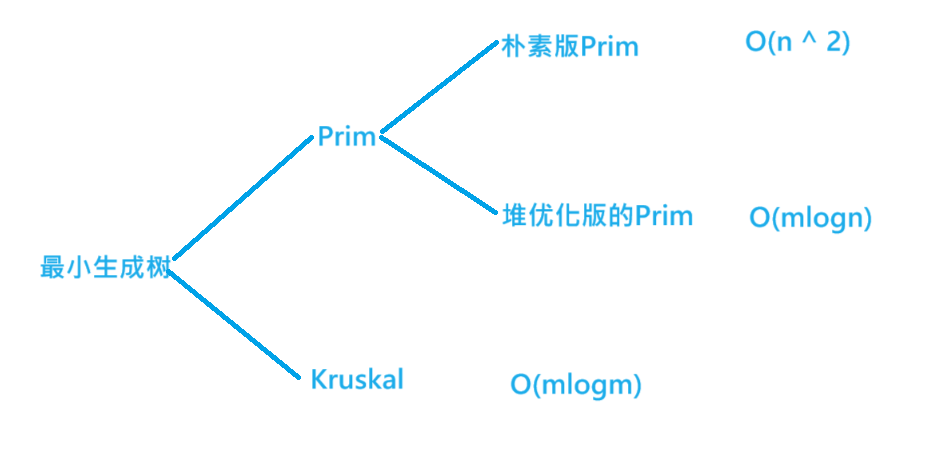
稠密图用Prim算法，稀疏图用Kruskal算法，堆优化版的Prim一般不会用到，所以我也就不写了。
最小生成树正负边都可以，没有环。

二、Prim算法

思想：遍历不在集合里的距离集合最近的点，把这个点加入集合，在用这个点更新其他点到集合的距离，重复直至所有点加入到集合中

题目描述：

给定一个 n 个点 m 条边的无向图，图中可能存在重边和自环，边权可能为负数。

求最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

给定一张边带权的无向图 G=(V,E)，其中 V 表示图中点的集合，E 表示图中边的集合，n=|V|，m=|E|。

由 V 中的全部 n 个顶点和 E 中 n?1 条边构成的无向连通子图被称为 G 的一棵生成树，其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。

输入格式
第一行包含两个整数 n 和 m。
接下来 m 行，每行包含三个整数 u,v,w，表示点 u 和点 v 之间存在一条权值为 w 的边。

输出格式
共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出impossible。

数据范围
1≤n≤500,1≤m≤105,图中涉及边的边权的绝对值均不超过 10000。

输入样例：
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例：
6

示例代码：

#include <cstdio>
#include <cstring>
#include <iostream>

using namespace std;

const int N = 510, INF = 0x3f3f3f3f;

int n, m;
int g[N][N];
int dist[N];
bool st[N];

int Prim()
{
    memset(dist, 0x3f, sizeof dist);
    
    int res = 0;
    for(int i = 0; i < n; ++i)
    {
        int t = -1;
        for(int j = 1; j <= n; ++j)
            if(!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
                
        if(i && dist[t] == INF) return INF;  //如果说不是第一个点，最短距离还为INF的话，说明无解
        
        if(i) res += dist[t];  //除过第一个加入集合的点
        st[t] = true;
        
        for(int j = 1; j <= n; ++j) dist[j] = min(dist[j], g[t][j]);  //通过t点更新其它点到集合的距离
    }
    
    return res;
}

int main()
{
    scanf("%d%d", &n, &m);
    
    memset(g, 0x3f, sizeof g);  //初始化图
    
    while(m--)
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        g[a][b] = g[b][a] = min(g[a][b], c);  //处理无向边、重边
    }
    
    int t = Prim();
    
    if(t == INF) puts("impossible");
    else printf("%d\n", t);
    
    return 0;
}

三、Kruskal算法

Prim算法是遍历点，而Kruskal算法是遍历边
思想：按边的权重从小到大遍历所有的边，a->b，若a和b不在同一个集合里，那就将他们合并到一个集合中

题目描述：

给定一个 n 个点 m 条边的无向图，图中可能存在重边和自环，边权可能为负数。

求最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

给定一张边带权的无向图 G=(V,E)，其中 V 表示图中点的集合，E 表示图中边的集合，n=|V|，m=|E|。

由 V 中的全部 n 个顶点和 E 中 n?1 条边构成的无向连通子图被称为 G 的一棵生成树，其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。

输入格式
第一行包含两个整数 n 和 m。
接下来 m 行，每行包含三个整数 u,v,w，表示点 u 和点 v 之间存在一条权值为 w 的边。

输出格式
共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出impossible。

数据范围
1≤n≤105,1≤m≤2?105,图中涉及边的边权的绝对值均不超过 1000。

输入样例：
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例：
6

代码示例：

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1e5+10, M = N * 2, INF = 0x3f3f3f3f;

int n, m;
int p[N];

struct Edge
{
    int a, b, w;
    
    bool operator<(const Edge& other)
    {
        return w < other.w;
    }
}edges[M];

int find(int x)
{
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int kruskal()
{
    for(int i = 1; i <= n; ++i) p[i] = i;  //初始化并查集
    
    sort(edges, edges + m);
    
    int res = 0, cnt = 0;
    for(int i = 0; i < m; ++i)
    {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;
        
        a = find(a), b = find(b);
        if(a != b)
        {
            p[a] = b;
            res += w;
            cnt++;
        }
    }
    
    if(cnt < n - 1) return INF;
    return res;
}

int main()
{
    scanf("%d%d", &n, &m);
    
    for(int i = 0; i < m; ++i)
    {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        edges[i] = {a,b,w};
    }
    
    int t = kruskal();
    
    if(t == INF) puts("impossible");
    else printf("%d\n", t);
    
    return 0;
}