贪心算法：活动选择问题以及贪心选择性质证明

什么时候使用贪婪算法?

– 贪心选择特性:

全局的最优解可以通过局部的最优（贪婪） 选择得到.

? 动态规划需要检查子问题的解。

– 最优子结构: 问题的最优解包含了其子问题的最优解.

? 例如, 如果 A 是S的最优解, 那么 A ' = A - {1} 是 的最优解.

? 贪心算法 (试探) 并不能总是得到最优解.

? 谈论算法和动态规划 (DP)对比

– 相同: 最优子结构

– 差别: 贪婪选择特性

– 如果贪婪算法不是最优的， 可以使用DP 。

活动选择问题

给定一个集合 S = {1, 2, …, n} n个计划的活动,对每个活动 ， 开始时间为 ?结束时间为 , 选择出相互兼容的活动最大集合.

– 如果被选中,活动 ?在半开放的区间中进行.

– 活动 ?和兼容 如果? 和? 不重叠

问题分析

基本思想

?对应伪代码

贪心选择性质证明

设为问题所给的活动集合，且E中的活动是按照活动结束时间增序排列的，明显，活动为最早结束。

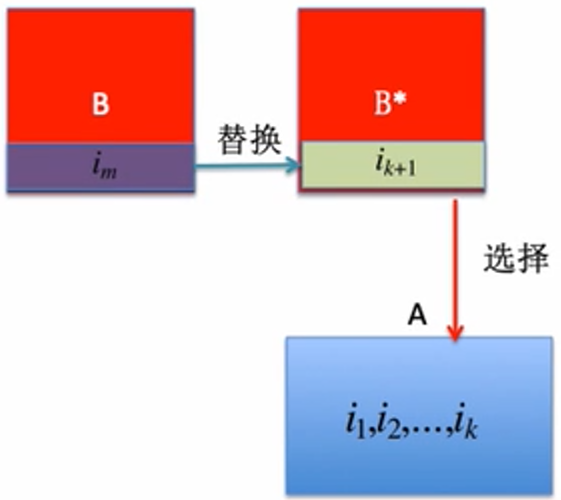
设A是问题的一个最优解，明显有A是E的一个子集。这里设A的第一个活动为k

1：若，即A的第一个活动就是最早结束的，故A是以贪心选择开始的最优解。

2：若，设集合，即用活动替换掉活动

又因为的结束时间小于，故比提取结束。另外由于A中的活动是相容的，故B中的活动也相容。

又因为A中的活动个数和B中的活动个数相同，故B也是最优解(需要注意的是最优解一般不唯一)。

所以B是一个以贪心选择活动为开始后的最优活动。

之后假设第k步成立，即按照算法选了，现在我们只要证明选

也是最优解解一部分即可。这是需要注意的是，对需要满足相同性，且是选结束时间尽可能早的任务.

利用数学归纳法

1：A包含了算法选择的前k项活动，假设存在活动选择的最优解的即
，如下图所示。

这里将未被选择的活动非为S1和S2两个部分。

值得注意的是，B一定来自于S1，因为S2的所有活动都与A冲突，为了满足相容性，不能被选到。

假设B不是S1的最优解，即S1存在有最优解B'的活动数多于B；

那么第k步的最优解就变为AUB'，显然与开始AUB为最优解的假设是矛盾的，因此不成立。

2：证明选结束时间最早的活动，也是最优解。

在S1中，必定存在一个结束时间最早的活动，即

在A的第一个活动为k时的证明可知，算法的第一步的最优解包含结束时间最早的活动。

因此S1存在最优解B*包含了活动。B和B*都是S1的最优解。因此两者包含的活动个数相同。

用B*代替B，即AUB的活动与AUB*的活动个数相同，因此最优解的性质不变。

而B*包含了，故证明了AUB*是最优的，所以根据数学归纳法，假设算法的前k项活动是最优的，选第k+1项也是最优解，命题得证。