leetcode 450. 删除二叉搜索树中的节点
发布时间:2023年12月20日
题目
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
首先找到需要删除的节点;
如果找到了,删除它。
示例 1: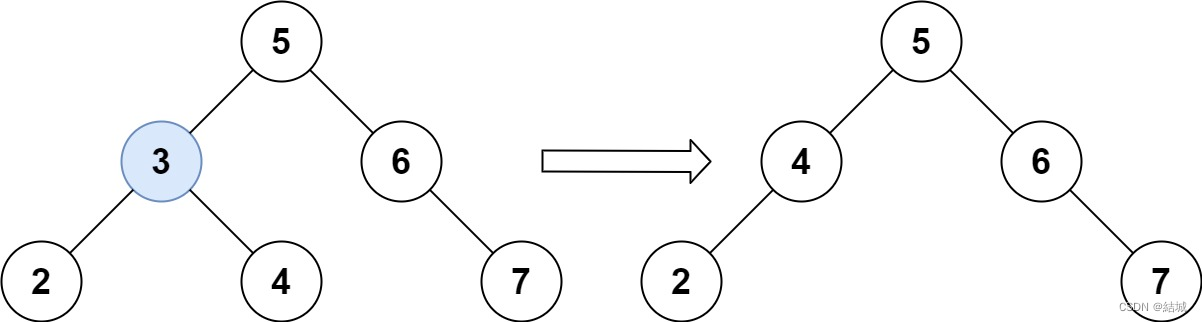
输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0
输出: []
提示:
节点数的范围 [0, 104].
-105 <= Node.val <= 105
节点值唯一
root 是合法的二叉搜索树
-105 <= key <= 105
进阶: 要求算法时间复杂度为 O(h),h 为树的高度。
思路
这题递归好做,迭代比较复杂。主要是要想清楚分哪些情况。没找到就根据值往左或右搜,找到了就分好几种情况了。
- 是叶子节点,那就直接返回空给上层就行了
- 节点左子树为空,那就返回右子树
- 节点右子树为空,那就返回左子树
- 左右子树都不为空,那我们需要想想逻辑了。其实当前根节点右侧是都大于它左侧是都小于它,那就让左侧最大的接到右侧最小的左边就行了。所以有如下代码
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null) {
return null;
}
if (root.val < key) {root.right = deleteNode(root.right, key);}
else if (root.val > key) {root.left = deleteNode(root.left, key);}
else {
if (root.left == null && root.right == null) {return null;}
else if (root.right == null) {return root.left;}
else if (root.right == null) {return root.right;}
else {
TreeNode cur = root.right;
while (cur.left != null) {
cur = cur.left;
}
cur.left = root.left;
return root.right;
}
}
// 树里没查到的
return root;
}
}
文章来源:https://blog.csdn.net/pige666/article/details/135095869
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 蓝桥oj3272小蓝的漆房
- 【MATLAB】EEMD_LSTM神经网络时序预测算法
- TiDB原理第一篇
- yolov5分割模型容易出错的点。
- 企业数据挖掘平台哪家好?听听客户的真实反馈
- Android 车联网——CarPackageManagerService介绍(十一)
- List集合知识总结
- 如何写出高质量的函数?快来学习这些coding技巧
- AI 绘画StableDiffusionWebui图生图
- 3 -灰度变换和空间滤波