力扣40. 组合总和 II(java 回溯法)
Problem: 40. 组合总和 II
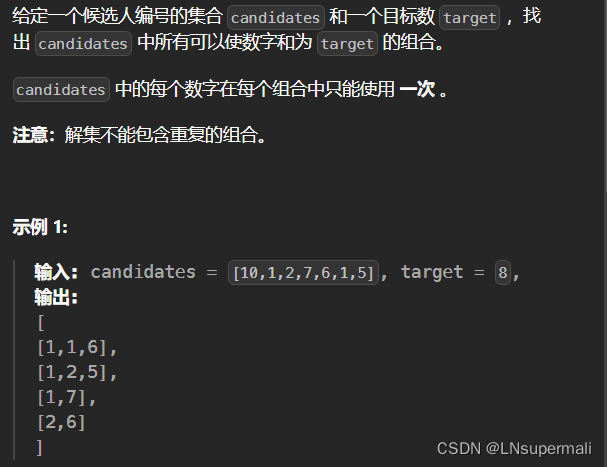
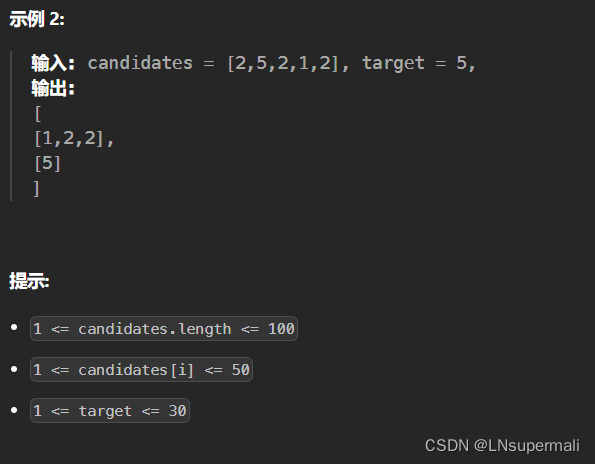
题目描述
思路
在使用回溯之前我们首先可以明确该题目也是一种元素存在重复但不可复用的组合类型问题。而此题目可以参考下面一题的大体处理思路:
Problem: 90. 子集 II
具体的:
1.首先对给定的数组排序
2.我们要记录一个决策路径path,一个路径和pathSum,我们在回溯的过程中若当前的路劲和pathSum等于给定的target时我们将当前的决策路径添加到结果集和中并返回;若路径和pathSum在递归过程中大于了target则直接返回;
3.在回溯函数中我们每次循环开始穷举,起始位置(i)为当前的决策阶段(start),并判断若i > start && candidates[i] == candidates[i - 1]此处的candidates为回溯函数中的可选列表,则不递归达到去重的效果,最后恢复当前决策路径path与路径和pathSum
解题方法
1.定义二维结果集合result,决策路径path,路径和pathSum
2.对给定数组排序
3.编写调用回溯函数,初始决策阶段为0:3.1当前的路劲和pathSum等于给定的target时我们将当前的决策路径添加到结果集和中并返回;若路径和pathSum在递归过程中大于了target则直接返回;
3.2for循环穷举,起始位置i为当前的决策阶段start,并判断若i > start && candidates[i] == candidates[i - 1],c则continue,不递归该分支
3.3每次将当前可选列表上的值添加到路径值pathSum,并递归调用,最后恢复当前决策路径,和路径和
复杂度
时间复杂度:
O ( n × 2 n ) O(n \times 2^n) O(n×2n)
空间复杂度:
O ( n ) O(n) O(n)
Code
class Solution {
//Result list
private List<List<Integer>> result = new ArrayList<>();
//Decision path
private List<Integer> path = new ArrayList<>();
//Recode the sum of path
private int pathSum = 0;
/**
* Gets all and a subset of the specified values
*
* @param candidates Specific list
* @param target target
* @return List<List < Integer>>
*/
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
Arrays.sort(candidates);
backtrack(candidates, 0, target);
return result;
}
/**
* Solve for all subsets of specified values using backtracking
*
* @param candidates Optional list
* @param start Decision stage
* @param target target
*/
private void backtrack(int[] candidates, int start, int target) {
//End condition
//if the pathSum equals the target
if (pathSum == target) {
result.add(new ArrayList<>(path));
return;
}
//End condition
//If the path bigger than target
if (pathSum > target) {
return;
}
for (int i = start; i < candidates.length; ++i) {
if (i > start && candidates[i] == candidates[i - 1]) {
continue;
}
path.add(candidates[i]);
pathSum += candidates[i];
backtrack(candidates, i + 1, target);
//Recover the current Decision Path of path
path.remove(path.size() - 1);
pathSum -= candidates[i];
}
}
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- VR看车,让购车变得更加“一目了然”
- 一天吃透MySQL面试八股文
- spring boot使用配置文件对静态变量进行赋值
- 第六章 树和二叉树
- js中三种URI编码方式比较
- 【满分】【华为OD机试真题2023C&D卷 JAVA&JS】反射计数
- 2023 波卡年度报告选读:Polkadot SDK 与开发者社区
- unity exe程序置顶和全屏
- 数据分析-Pandas如何整合多张数据表
- 在检验铸铁平台精度时应注意哪些问题