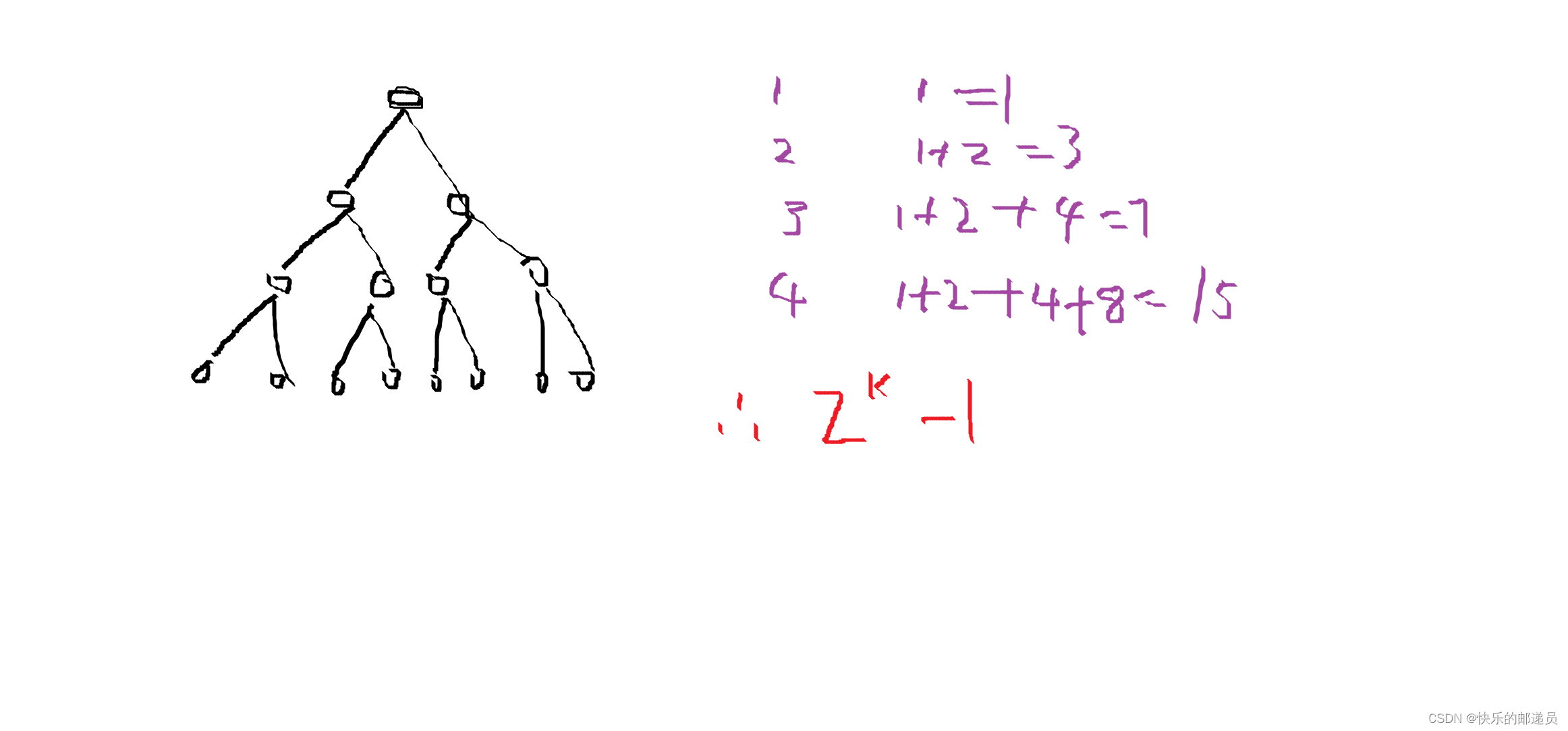第六章 树和二叉树

树：非线性结构

在树结构中，节点间关系是前驱唯一而后继不唯一，即节点之间是一对多的关系

树结构是指具有分支关系的结构，树结构应用广泛，特别是在大量数据处理方面显得更加突出。

任何数都可以转化为二叉树

二叉树：1.每个节点的度都不大于2；

? ? ? ? ? ? ? 2.每个节点的孩子节点次序不能任意颠倒（即有序树）

完全二叉树：1.叶子结点只可能出现在最后两层

? ? ? ? ? ? ? ? ? ? ? 2.度为1的结点个数为0或1

满二叉树必定为完全二叉树，而完全二叉树不一定为满二叉树

二叉树的性质（常用）：

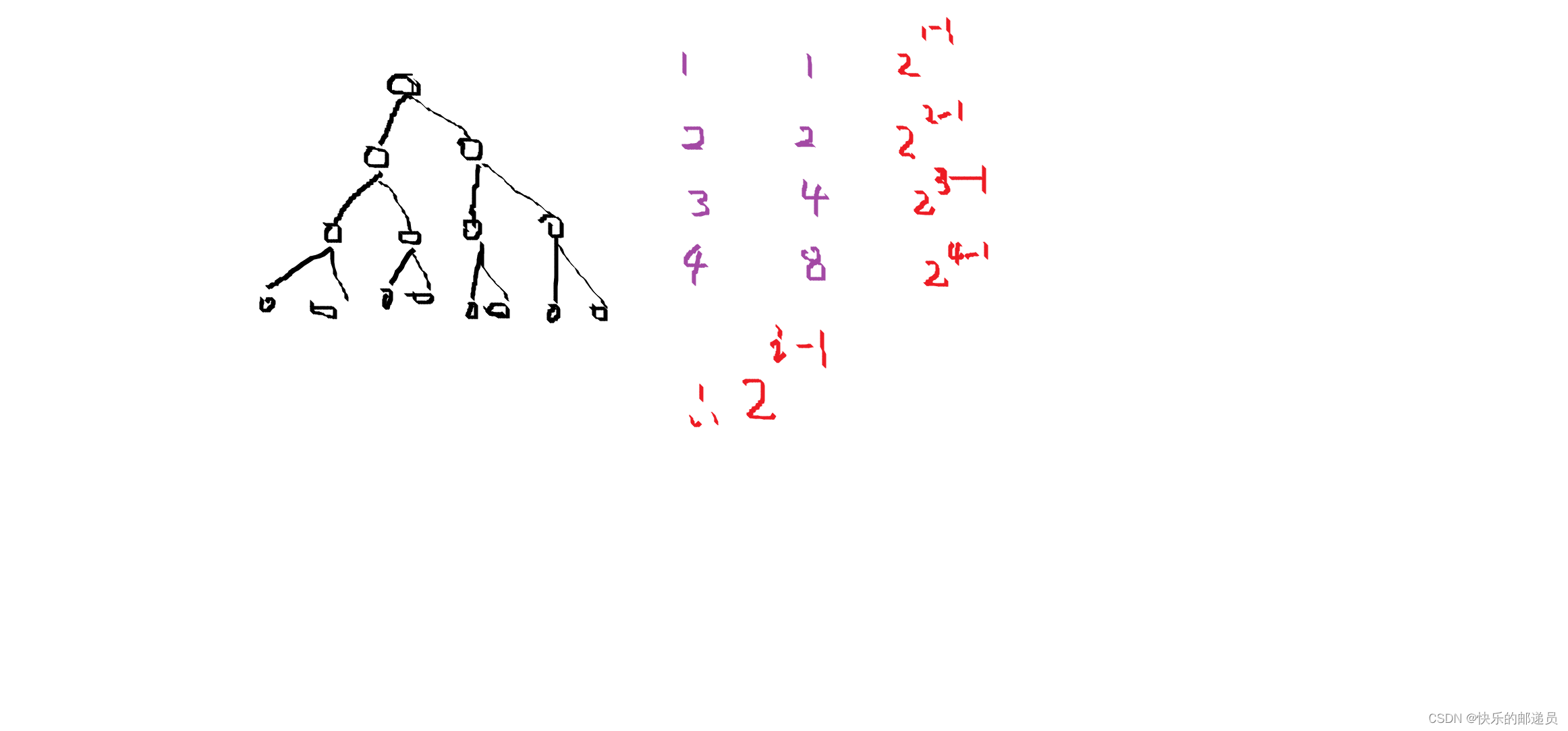
? ? ? ? ? ? ? ? 1.在二叉树的第i层上至多有2^(i-1)个节点（i>=1）

? ? ? ? ? ? ? ? 2.深度为k的二叉树至多有2^k-1个节点（k>=1）

? ? ? ? ? ?3.对于任意一颗二叉树T,若终端结点数为n0,二其度数为2的结点数为n2,则n0=n2+1

? ? ? ? ? 4.具有n个节点的完全二叉树的深度为【】+1

? ? ? ? ? （ps:【】：向下取整,可与定理二结合下）

常用的有关树的知识：

1.二叉树的存储结构：顺序存储结构和链式存储结构

2.若一个二叉树含有n个节点，则其二叉链表中必含有2n个指针域，其中必有n+1个空的链域，n-1个非空的链域

3.前序+后序并不一定能唯一确定二叉树

4.前序+中序? 或者? ?中序+后序可以唯一?确定一个二叉树

5. 树的先根遍历《=》转换后二叉树的先序遍历

? ? ?树的后根遍历《=》转换后二叉树的中序遍历

6.哈夫曼树不唯一，哈夫曼编码不唯一

一、判断题

1.完全二叉树中，若一个结点没有左孩子，则它必是树叶。（T）

ps：叶子结点度为0，若完全二叉树中，若没有左结点，则一定没有右结点

?2.某二叉树的后序和中序遍历序列正好一样，则该二叉树中的任何结点一定都无右孩子。（T）

后序遍历：左 右 root

中序遍历：左 root 右

所以：若后序遍历和中序遍历正好一样，则都无右孩子

后序遍历：左 root? ? 中序遍历：左 root

?3.已知一棵二叉树的先序遍历结果是ABC,　则CAB不可能是中序遍历结果。(T)

先序遍历：root 左 右? ? A? B? C

中序遍历：左?root? 右? ?B A? C

4.?将一棵完全二叉树存于数组中（根结点的下标为1）。则下标为23和24的两个结点是兄弟。(F)

下标从1开始，2n和2n+1为兄弟，例如 24?和25为兄弟，22和23为兄弟

5.?若一个结点是某二叉树的中序遍历序列的最后一个结点，则它必是该树的前序遍历序列中的最后一个结点。（F）

中序遍历：LDR

前序遍历：DLR

若R不存在，则错 ,因为LD? 的最后一个结点为D? ? ?DL的最后一个结点为L

6.?哈夫曼编码是一种最优的前缀码。对一个给定的字符集及其字符频率，其哈夫曼编码不一定是唯一的，但是每个字符的哈夫曼码的长度一定是唯一的。（F）

哈夫曼字符的频率相同时每个字符的码长不是确定的

二、单选题

1.树最适合于用来表示（D）

A.有序数据元素

B.无序数据元素

C.元素之间无联系的数据

D.元素之间具有分支层次关系的数据

2.以二叉链表作为二叉树的存储结构，在具有?n?个结点的二叉链表中（n>0），空链域的个数为 _(A)

A.n+1

B.n

C.n?1

D.无法确定

3.由分别带权为9、2、5、7的四个叶子结点构成一棵哈夫曼树，该树的带权路径长度为：(C)

A.23

B.37

C.44

D.46

?4.AVL树是一种平衡的二叉搜索树，树中任一结点具有下列哪一特性：(B)

A.左、右子树的高度均相同

B.左、右子树高度差的绝对值不超过1

C.左子树的高度均大于右子树的高度

D.左子树的高度均小于右子树的高度

5.已知字符集{ a, b, c, d, e, f, g, h }。若各字符的哈夫曼编码依次是 0100, 10, 0000, 0101, 001, 011, 11, 0001，则编码序列 0100011001001011110101 的译码结果是：(D)

A.acgabfh

B.adbagbb

C.afbeagd

D.afeefgd

?按照给定的编码找到合适的数字

0100??011??001? 001??011? ? ?11??0101

0100（a）011(f) 001(e)? 001(e) 011(f) 11(g)? 0101(d)? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??

6.已知二叉树的先序遍历序列为ABCDEFGH，中序遍历序列为CBEDFAGH，则该二叉树形态中，父节点的右子节点为（C）。

A.D

B.H

C.G

D.F

?先看先序遍历a为根节点，再中序遍历，GH为右子树，再看先序遍历,G在前面，所以父节点的右子节点为G

7.?若将一棵树?T?转化为对应的二叉树?BT，则下列对?BT?的遍历中，其遍历序列与?T?的后根遍历序列相同的是：(B)

A.先序遍历

B.中序遍历

C.后序遍历

D.按层遍历

?8.给定二叉树如下图所示。设N代表二叉树的根，L代表根结点的左子树，R代表根结点的右子树。若遍历后的结点序列为3、1、7、5、6、2、4，则其遍历方式是：(B)

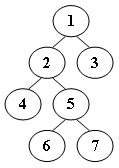
A.NRL

B.RNL

C.LRN

D.RLN

9.任何一棵二叉树的叶结点在先序、中序和后序遍历序列中的相对次序(B)

A.发生改变

B.不发生改变

C.不能确定

D.以上都不对

10.二叉树中第5层（根的层号为1）上的结点个数最多为：(C)

A.8

B.15

C.16

D.32

在第i层上至多有2^(i-1)个结点，即2^（5-1）=2^4=16

?11.一棵二叉树的先序序列：abdfcegh，中序序列：bfdagehc。该二叉树中右子树的根结点是（C）。

A.a

B.b

C.c

D.d

已知根节点为a,看中序序列，gehc为其右子树，再从先序遍历找cegh,发现c在最前面，则右子树的根节点为c

12.?一棵二叉树中有7个度为2的结点和5个度为1的结点，其总共有（C ）个结点。

A.16

B.18

C.20

D.30

度为0的结点个数=度为2的结点个数+1

即0:8 1:5 2:7

所以总结点的个数为：7+5+8=20

13.?若一棵完全二叉树有2001个结点，则该二叉树叶结点的个数是(C )。

A.999

B.1000

C.1001

D.1002

完全二叉树有2001个节点

树叶节点即度为0的结点，假设有x个，则度为2的结点的个数为x-1个

所以x+x-1=2001，解得x=2002/2=1001

三、填空题?

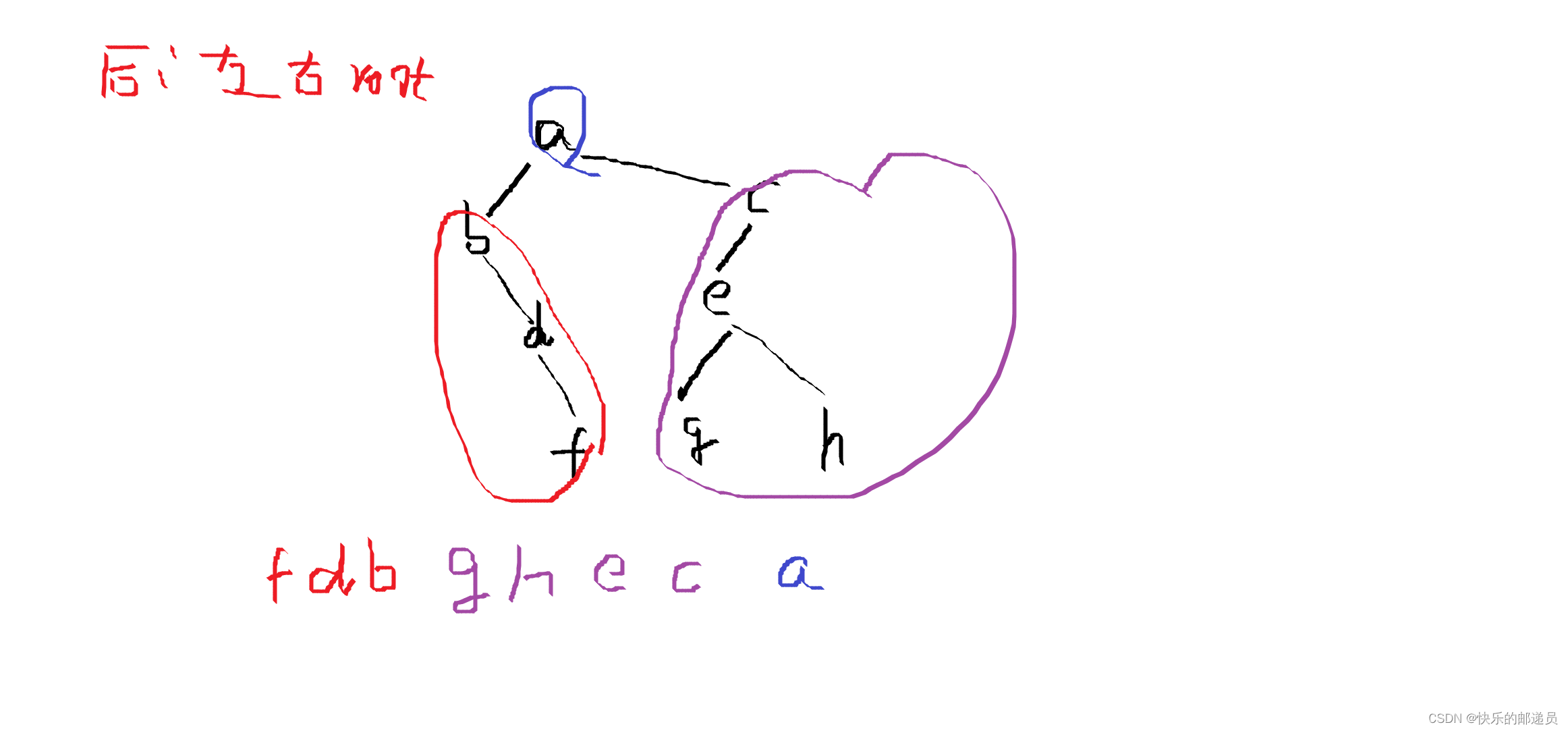
1.一棵二叉树的先序序列： abdfcegh，中序序列：bfdagehc。后序遍历序列为（ fdbgheca）。

2.若以{4，5，6，7，8}作为叶子结点的权值构造哈夫曼树，则其带权路径长度是（69）