数据结构和算法-算法的基本概念和时间复杂度和空间复杂度

发布时间：2024年01月02日

文章目录

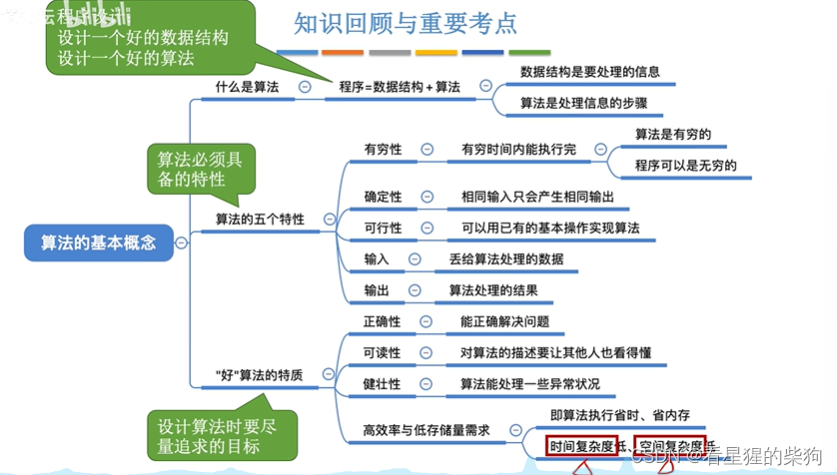
算法的基本概念

总览

在这里插入图片描述

什么是算法

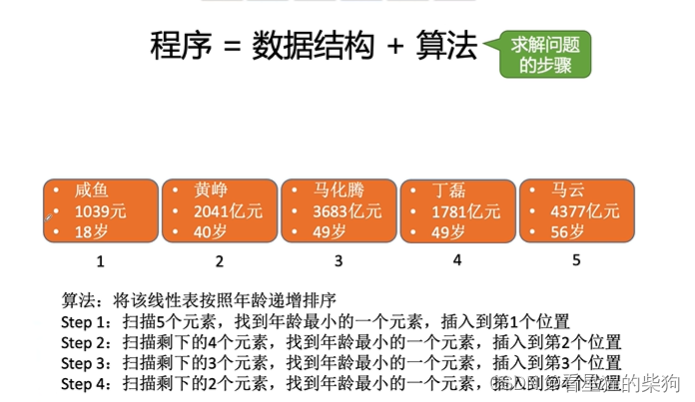
算法就是处理的步骤
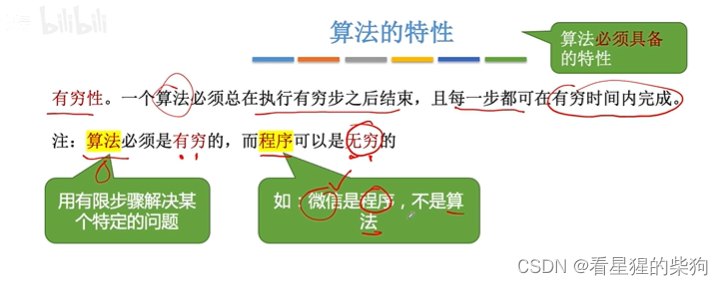
在这里插入图片描述
在这里插入图片描述

算法的特性

程序可以一直运行，所以说是无穷的
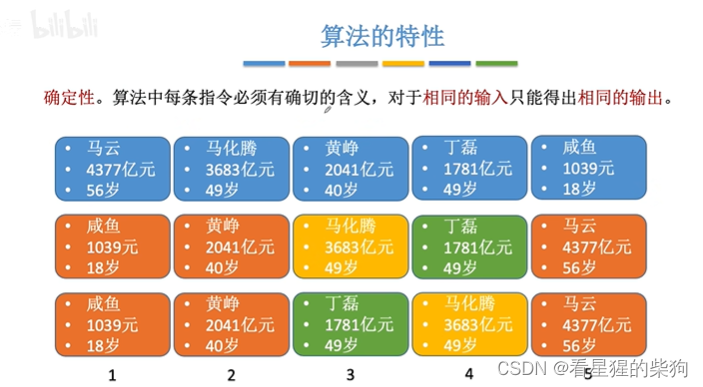
在这里插入图片描述
不能出现两种不同的结果出来，必须对于相同输入只有相同输出
如下图中出现两个相等时可做一个处理使得结果唯一
在这里插入图片描述
注意输入和输出的个数
在这里插入图片描述
只要一个特性不满足，就不能称之为算法

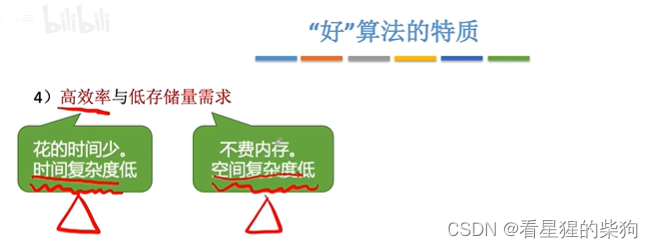
好算法的特质

正确性即结果是正确的
在这里插入图片描述
可读性即有些注释啥的，让别人能看懂
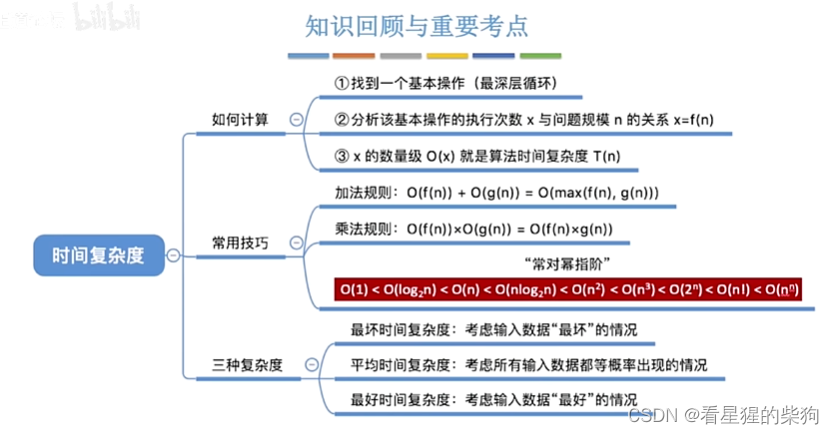
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

小结

在这里插入图片描述

算法的时间复杂度

如何评判算法时间开销

如果让算法在机器上运行，然后在结束后再统计其时间，那么会由于机器不同，执行算法的语言不同 ，编译程序的效率会有不同的结果
并且由于某些算法是不能等运行后再去统计其运行时间的，所以由算法先运行再去统计运行时间是不合理的
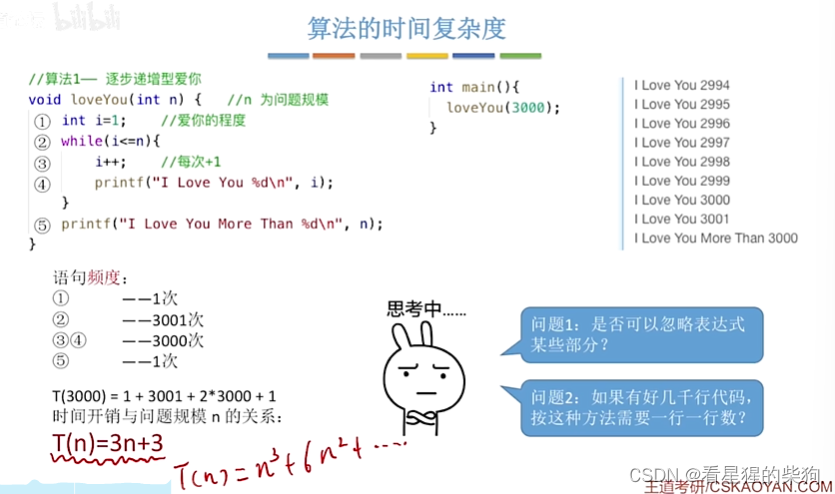
在这里插入图片描述

计算算法时间复杂度

当统计每条语句执行的次数时，得到为3n+3的算法时间复杂度
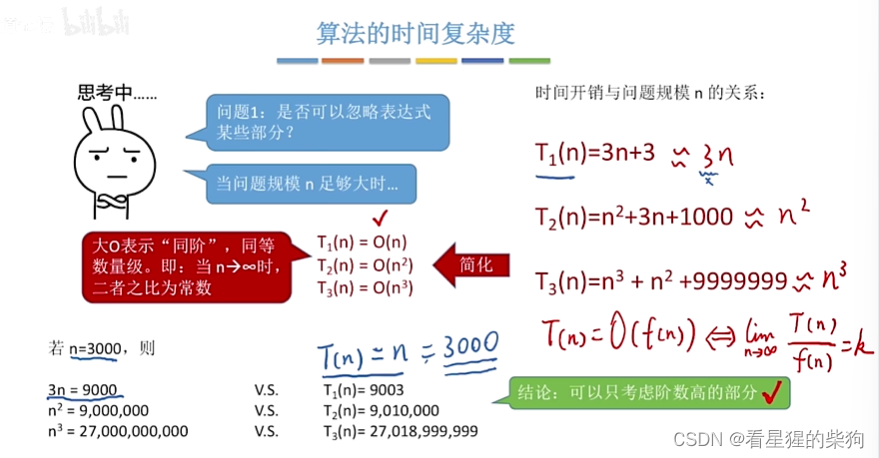
当程序语句过多时，算法时间复杂度表达式过于复杂时，该如何处理
在这里插入图片描述

忽略表达式的某些部分

可以通过洛必达证明
在这里插入图片描述
递增大小，对应的图
记住口诀 常对幂指阶
在这里插入图片描述
注意如何计算的和大O的含义

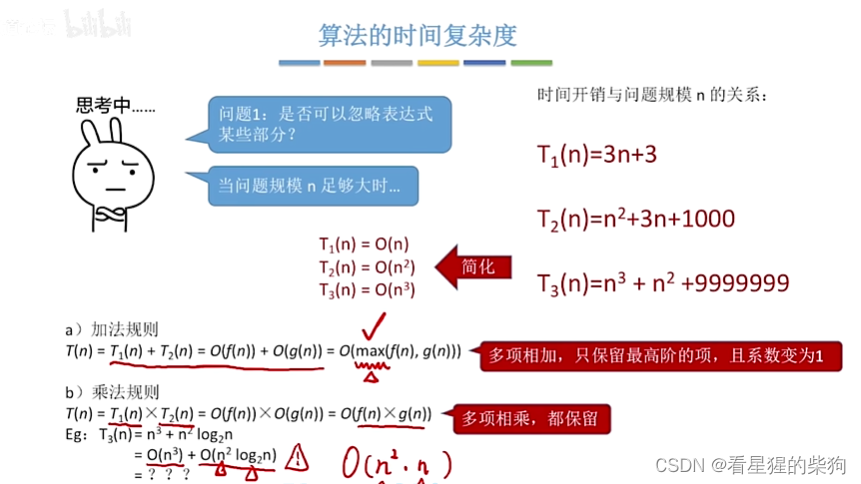
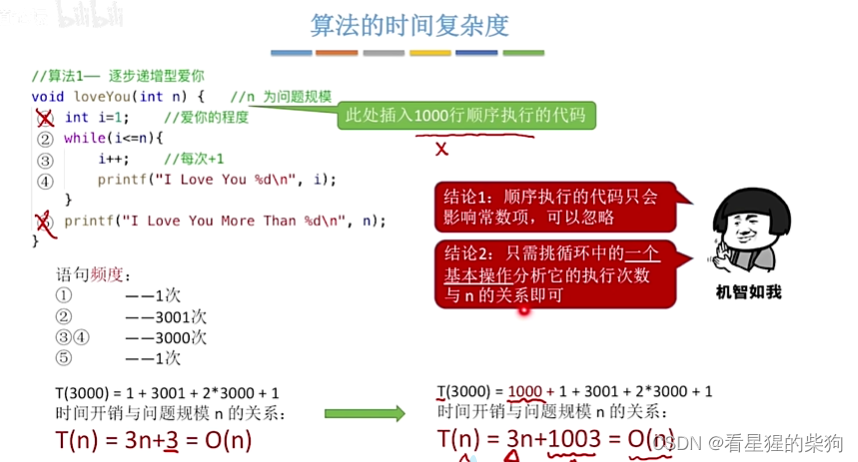
在这里插入图片描述
计算规则
在这里插入图片描述

是否要一行一行数代码

顺序执行的代码只会影响常数项，所以不考虑
而循环里的多个操作也是影响n的系数，所以不考虑，只需考虑循环的一个操作执行次数即可
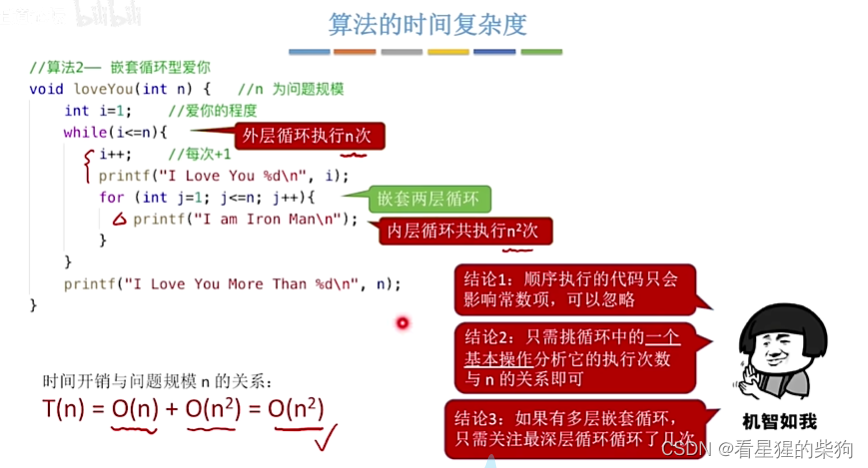
在这里插入图片描述
当有多层循环是，表层循环对于深层循环可忽略不计
所以考虑最深层循环的执行次数即可
在这里插入图片描述

小练习1

首先找到循环终止条件，在计算循环次数
在这里插入图片描述

小练习2

输入的查找的数不一样，此时对于的循环不一样，一般计算的时间复杂度都是平均时间复杂度
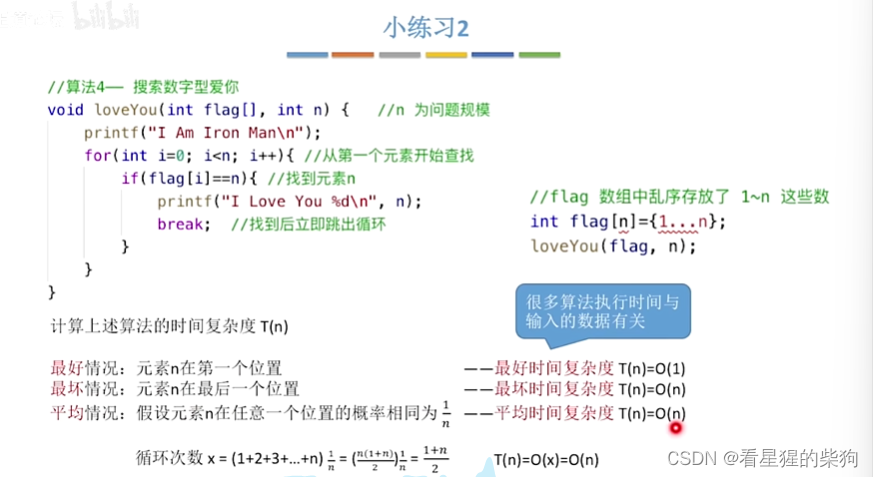
在这里插入图片描述

最坏时间复杂度和平均时间复杂度

在这里插入图片描述

小结

算法的性能问题只有在n很大才会暴露出来
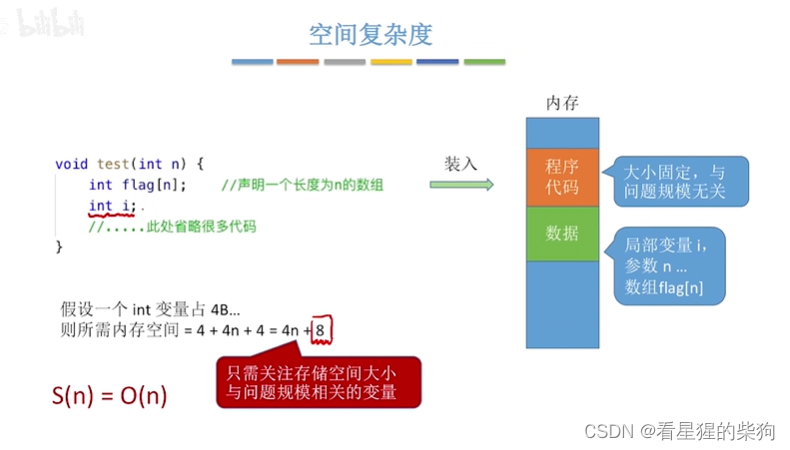
在这里插入图片描述

算法的空间复杂度

程序运行时的内存需求

大小固定，与问题规模无关就是说所占空间大小不会随着输入变化而变化
原地工作即空间复杂度为常数
在这里插入图片描述
此时当n趋向很大时，可忽略常数级，占空间与问题规模相关变量有关
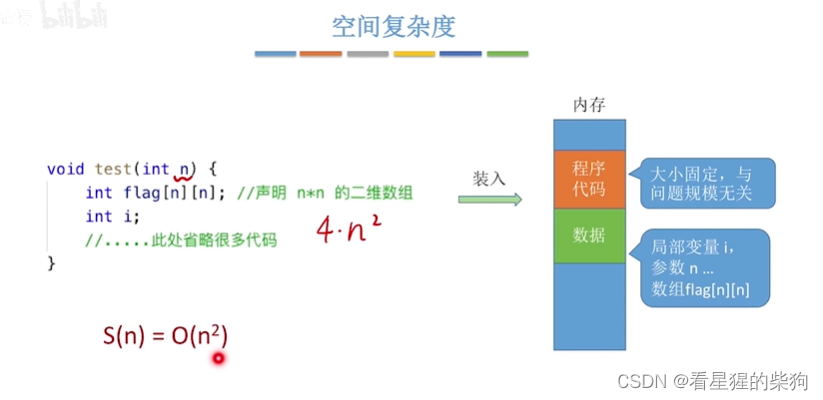
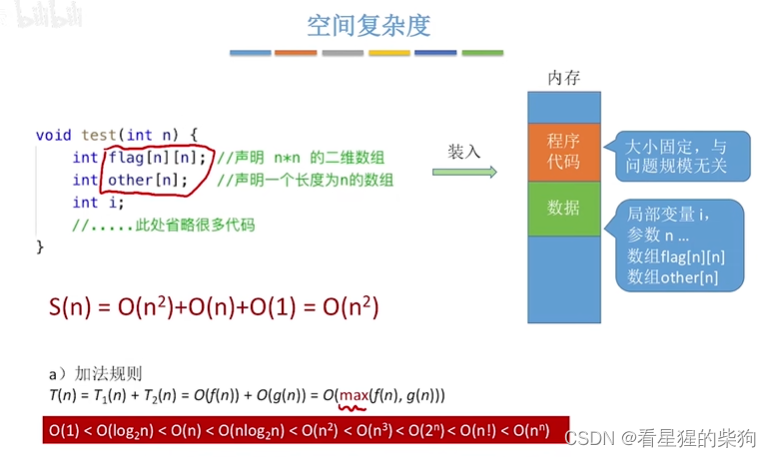
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

函数递归的空间复杂度

每层调用中要用到的参数和局部变量需要增加存储空间来存储
可参考函数调用栈存储保存恢复函数栈信息的内容和相关该函数的局部变量和参数等内容
每层递归进入函数后需要的空间是固定的（下图是固定的），作为系数可忽略
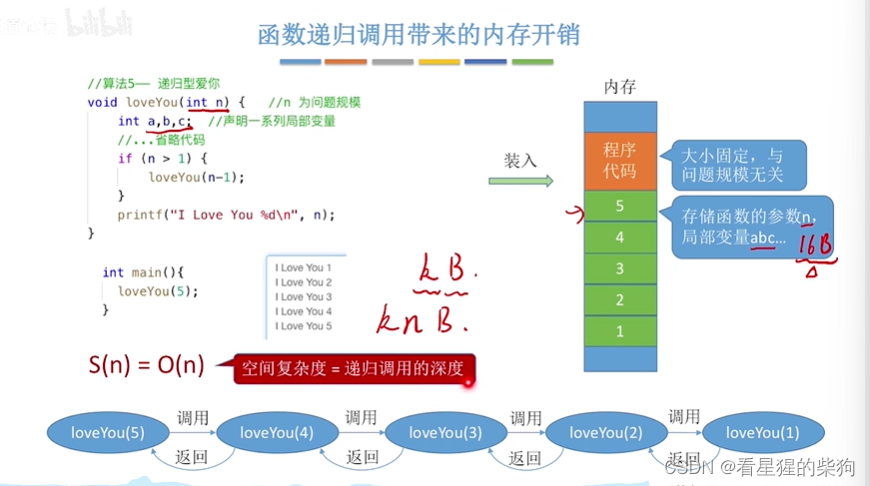
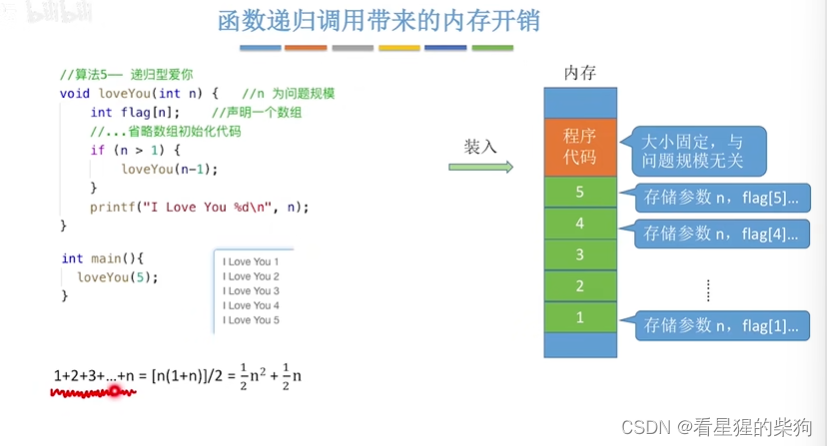
在这里插入图片描述
此时递归每层调用函数的所占空间与传入的参数有关，所以需要的空间不是固定的
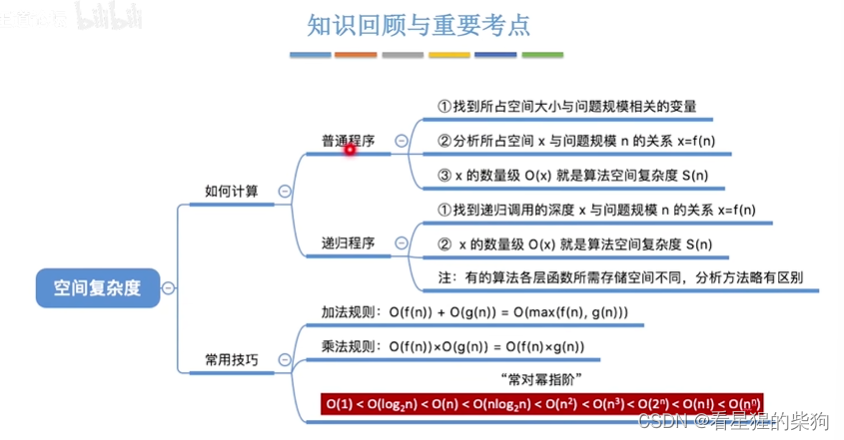
在这里插入图片描述

小结

在这里插入图片描述

文章来源:https://blog.csdn.net/llovewuzhengzi/article/details/135333560
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章