【无标题】

CGAL 5.4.5 - Surface Mesh: User Manual

1、Kruskal计算最小生成树

#include <CGAL/Simple_cartesian.h>
#include <CGAL/Surface_mesh.h>
#include <boost/graph/kruskal_min_spanning_tree.hpp>
#include <iostream>
#include <fstream>
#include <list>
typedef CGAL::Simple_cartesian<double>                       Kernel;
typedef Kernel::Point_3                                      Point;
typedef CGAL::Surface_mesh<Point>                            Mesh;
typedef boost::graph_traits<Mesh>::vertex_descriptor vertex_descriptor;
typedef boost::graph_traits<Mesh>::vertex_iterator   vertex_iterator;
typedef boost::graph_traits<Mesh>::edge_descriptor   edge_descriptor;
/*
Surface_mesh 提供了四个嵌套类，分别代表半边数据结构的基本元素：

Surface_mesh::Vertex_index曲面网格::顶点索引
Surface_mesh::Halfedge_index曲面网格::半边索引
Surface_mesh::Face_index曲面网格::面索引
Surface_mesh::Edge_index曲面网格::边索引

*/
void kruskal(const Mesh& sm)
{
    // 默认权重=边的平方长   存储Surace_mesh 的边信息
    std::list<edge_descriptor> mst;
    //9600->3199 边
    boost::kruskal_minimum_spanning_tree(sm,
        std::back_inserter(mst));
    std::cout << "#VRML V2.0 utf8\n"
        "Shape {\n"
        "  appearance Appearance {\n"
        "    material Material { emissiveColor 1 0 0}}\n"
        "    geometry\n"
        "    IndexedLineSet {\n"
        "      coord Coordinate {\n"
        "        point [ \n";
    
    //打印sm中所有顶点
    for (auto v : sm.vertices()) {
        std::cout << "        " << sm.point(v) << "\n";
    }
    //vertex_iterator vb, ve;
    //for (boost::tie(vb, ve) = vertices(sm); vb != ve; ++vb) {
    //    std::cout << "        " << sm.point(*vb) << "\n";
    //}
    std::cout << "        ]\n"
        "     }\n"
        "      coordIndex [\n";

    //对于每条边，它提取并打印出该边连接的两个顶点的索引。
    for (std::list<edge_descriptor>::iterator it = mst.begin(); it != mst.end(); ++it)
    {
        edge_descriptor e = *it;
        vertex_descriptor s = source(e, sm);
        vertex_descriptor t = target(e, sm);
        std::cout << "      " << s << ", " << t << ", -1\n";
    }
    std::cout << "]\n"
        "  }#IndexedLineSet\n"
        "}# Shape\n";
}
int main(int argc, char** argv)
{
    Mesh sm;
    std::string fname = argc == 1 ? CGAL::data_file_path("meshes/knot1.off") : argv[1];
    if (!CGAL::IO::read_polygon_mesh(fname, sm))
    {
        std::cerr << "Invalid input file." << std::endl;
        return EXIT_FAILURE;
    }
    kruskal(sm);
    return 0;
}

2、Prim的最小生成树?

还是之前的模型

好的，我将重点解释Prim算法的使用以及在代码中如何通过映射来存储Prim算法的结果。

Prim最小生成树算法

Prim算法是一种用于在带权无向图中找到最小生成树的算法。最小生成树是原图的一个子图，它连接了图中的所有顶点，且边的权重之和最小，且不形成任何循环。Prim算法的基本思想是：

1. 从图中的某个顶点开始。
2. 每次迭代中，选择连接树与非树顶点且权重最小的边，并将其添加到树中。
3. 重复此过程直到所有顶点都被包含在树中。

?

#include <CGAL/Simple_cartesian.h>
#include <CGAL/Surface_mesh.h>
#include <iostream>
#include <fstream>
// workaround a bug in Boost-1.54
#include <CGAL/boost/graph/dijkstra_shortest_paths.h>
#include <boost/graph/prim_minimum_spanning_tree.hpp>
typedef CGAL::Simple_cartesian<double>                       Kernel;
typedef Kernel::Point_3                                      Point;
typedef CGAL::Surface_mesh<Point>                            Mesh;
typedef boost::graph_traits<Mesh>::vertex_descriptor vertex_descriptor;
int main(int argc, char* argv[])
{
    Mesh sm;
    std::string fname = R"(C:\chenqi\ThridParty\CGAL-5.4.3\data\meshes\knot1.off)";
    if (!CGAL::IO::read_polygon_mesh(fname, sm))
    {
        std::cerr << "Invalid input file." << std::endl;
        return EXIT_FAILURE;
    }
    //声明了一个名为 predecessor 的属性映射。这个映射将每个顶点（vertex_descriptor）映射到另一个顶点（也是 vertex_descriptor）。
    //这种类型的映射通常用于存储诸如搜索算法中每个顶点的前驱顶点之类的信息。
    Mesh::Property_map<vertex_descriptor, vertex_descriptor> predecessor;
    predecessor = sm.add_property_map<vertex_descriptor, vertex_descriptor>("v:predecessor").first;
    //在计算完最小生成树后，代码遍历所有顶点，并使用 predecessor 映射来输出每个顶点与其前驱顶点之间的边。
    boost::prim_minimum_spanning_tree(sm, predecessor, boost::root_vertex(*vertices(sm).first));
    std::cout << "#VRML V2.0 utf8\n"
        "DirectionalLight {\n"
        "direction 0 -1 0\n"
        "}\n"
        "Shape {\n"
        "  appearance Appearance {\n"
        "    material Material { emissiveColor 1 0 0}}\n"
        "    geometry\n"
        "    IndexedLineSet {\n"
        "      coord Coordinate {\n"
        "        point [ \n";
    for (vertex_descriptor vd : vertices(sm)) {
        std::cout << "        " << sm.point(vd) << "\n";
    }
    std::cout << "        ]\n"
        "     }\n"
        "      coordIndex [\n";
    for (vertex_descriptor vd : vertices(sm)) {
        if (predecessor[vd] != vd) {
            std::cout << "      " << std::size_t(vd) << ", " << std::size_t(predecessor[vd]) << ", -1\n";
        }
    }
    std::cout << "]\n"
        "  }#IndexedLineSet\n"
        "}# Shape\n";
    sm.remove_property_map(predecessor);
    return 0;
}

?

命令行生成wrl
your_program > mst.wrl

下载可视化软件

Download FreeWRL VRML/X3D browser (sourceforge.net)

#include <iostream>
#include <CGAL/Simple_cartesian.h>
#include <CGAL/Surface_mesh.h>
typedef CGAL::Simple_cartesian<double> K;
typedef CGAL::Surface_mesh<K::Point_3> Mesh;
typedef Mesh::Vertex_index vertex_descriptor;
int main()
{
    Mesh m;
    Mesh::Vertex_index u;
    for (unsigned int i = 0; i < 5; ++i) {
        Mesh::Vertex_index v = m.add_vertex(K::Point_3(0, 0, i + 1));
        if (i == 2) u = v;
    }
    m.remove_vertex(u);
    std::cout << "After insertion of 5 vertices and removal of the 3. vertex\n"
        << "# vertices  / # vertices + # removed vertices = "
        << m.number_of_vertices()
        << " / " << m.number_of_vertices() + m.number_of_removed_vertices() << std::endl;
    std::cout << "Iterate over vertices\n";
    {
        for (vertex_descriptor vd : m.vertices()) {
            std::cout << m.point(vd) << std::endl;
        }
    }
    // The status of being used or removed is stored in a property map
    Mesh::Property_map<Mesh::Vertex_index, bool> removed
        = m.property_map<Mesh::Vertex_index, bool>("v:removed").first;
    std::cout << "\nIterate over vertices and deleted vertices\n"
        << "# vertices / # vertices + # removed vertices = "
        << m.number_of_vertices()
        << " / " << m.number_of_vertices() + m.number_of_removed_vertices() << std::endl;
    {
        unsigned int i = 0, end = m.number_of_vertices() + m.number_of_removed_vertices();
        for (; i < end; ++i) {
            vertex_descriptor vh(i);
            assert(m.is_removed(vh) == removed[vh]);
            std::cout << m.point(vh) << ((m.is_removed(vh)) ? "  R\n" : "\n");
        }
    }
    m.collect_garbage();
    std::cout << "\nAfter garbage collection\n"
        << "# vertices / # vertices + # removed vertices = "
        << m.number_of_vertices()
        << " / " << m.number_of_vertices() + m.number_of_removed_vertices() << std::endl;
    {
        unsigned int i = 0, end = m.number_of_vertices() + m.number_of_removed_vertices();
        for (; i < end; ++i) {
            vertex_descriptor vh(i);
            std::cout << m.point(vh) << ((m.is_removed(vh)) ? "  R\n" : "\n");
        }
    }
    return 0;
}

3、移除顶点垃圾回收

#include <iostream>
#include <CGAL/Simple_cartesian.h>
#include <CGAL/Surface_mesh.h>
typedef CGAL::Simple_cartesian<double> K;
typedef CGAL::Surface_mesh<K::Point_3> Mesh;
typedef Mesh::Vertex_index vertex_descriptor;
int main()
{
    Mesh m;
    Mesh::Vertex_index u;
    for (unsigned int i = 0; i < 5; ++i) {
        Mesh::Vertex_index v = m.add_vertex(K::Point_3(0, 0, i + 1));
        if (i == 2) u = v;
    }
    m.remove_vertex(u);
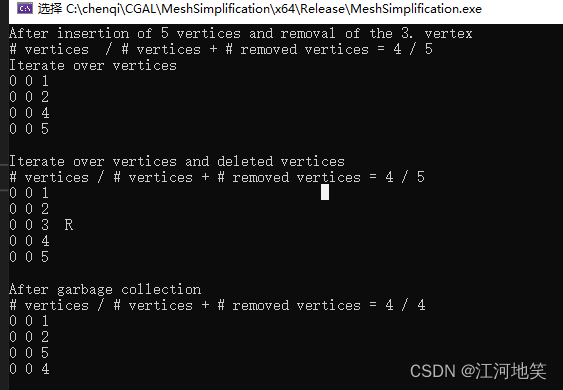
    std::cout << "After insertion of 5 vertices and removal of the 3. vertex\n"
        << "# vertices  / # vertices + # removed vertices = "
        << m.number_of_vertices()
        << " / " << m.number_of_vertices() + m.number_of_removed_vertices() << std::endl;
    std::cout << "Iterate over vertices\n";
    {
        for (vertex_descriptor vd : m.vertices()) {
            std::cout << m.point(vd) << std::endl;
        }
    }
    // The status of being used or removed is stored in a property map
    Mesh::Property_map<Mesh::Vertex_index, bool> removed
        = m.property_map<Mesh::Vertex_index, bool>("v:removed").first;
    std::cout << "\nIterate over vertices and deleted vertices\n"
        << "# vertices / # vertices + # removed vertices = "
        << m.number_of_vertices()
        << " / " << m.number_of_vertices() + m.number_of_removed_vertices() << std::endl;
    {
        unsigned int i = 0, end = m.number_of_vertices() + m.number_of_removed_vertices();
        for (; i < end; ++i) {
            vertex_descriptor vh(i);
            //这是一个断言语句，用于验证顶点vh的移除状态。m.is_removed(vh)返回一个布尔值，指示顶点是否被移除。
            //removed[vh]从之前创建的属性映射中获取该顶点的移除状态。断言确保这两种方式获取的信息是一致的。
            assert(m.is_removed(vh) == removed[vh]);
            //这行代码打印出顶点的坐标。如果顶点被移除（m.is_removed(vh)为true），则在坐标后面打印" R"（表示顶点被移除）。否则，只打印一个换行符。
            std::cout << m.point(vh) << ((m.is_removed(vh)) ? "  R\n" : "\n");
        }
    }

    //调用collect_garbage以清除被移除的顶点并优化网格内存使用。
    //再次遍历所有顶点，这次只包括未被移除的顶点。
    m.collect_garbage();
    std::cout << "\nAfter garbage collection\n"
        << "# vertices / # vertices + # removed vertices = "
        << m.number_of_vertices()
        << " / " << m.number_of_vertices() + m.number_of_removed_vertices() << std::endl;
    {
        unsigned int i = 0, end = m.number_of_vertices() + m.number_of_removed_vertices();
        for (; i < end; ++i) {
            vertex_descriptor vh(i);
            std::cout << m.point(vh) << ((m.is_removed(vh)) ? "  R\n" : "\n");
        }
    }
    return 0;
}