何为算法之时间复杂度
时间复杂度
同空间复杂度相比,时间复杂度的分析要复杂一些。时间复杂度是指运行算法所需要的计算工作量,记作:
T
(
n
)
=
O
(
f
(
n
)
)
T(n)=O(f(n))
T(n)=O(f(n))
简单理解,时间复杂度就是执行语句的次数。也就是说,时间复杂度高则运行时间长,时间复杂度低则运行时间短。常见的时间复杂度有
O
(
1
)
、
O
(
n
)
、
O
(
n
2
)
、
O
(
2
n
)
和
O
(
l
o
g
2
n
)
O(1)、O(n)、O(n^2)、O(2^n)和O(log_2n)
O(1)、O(n)、O(n2)、O(2n)和O(log2?n)等如下图所示
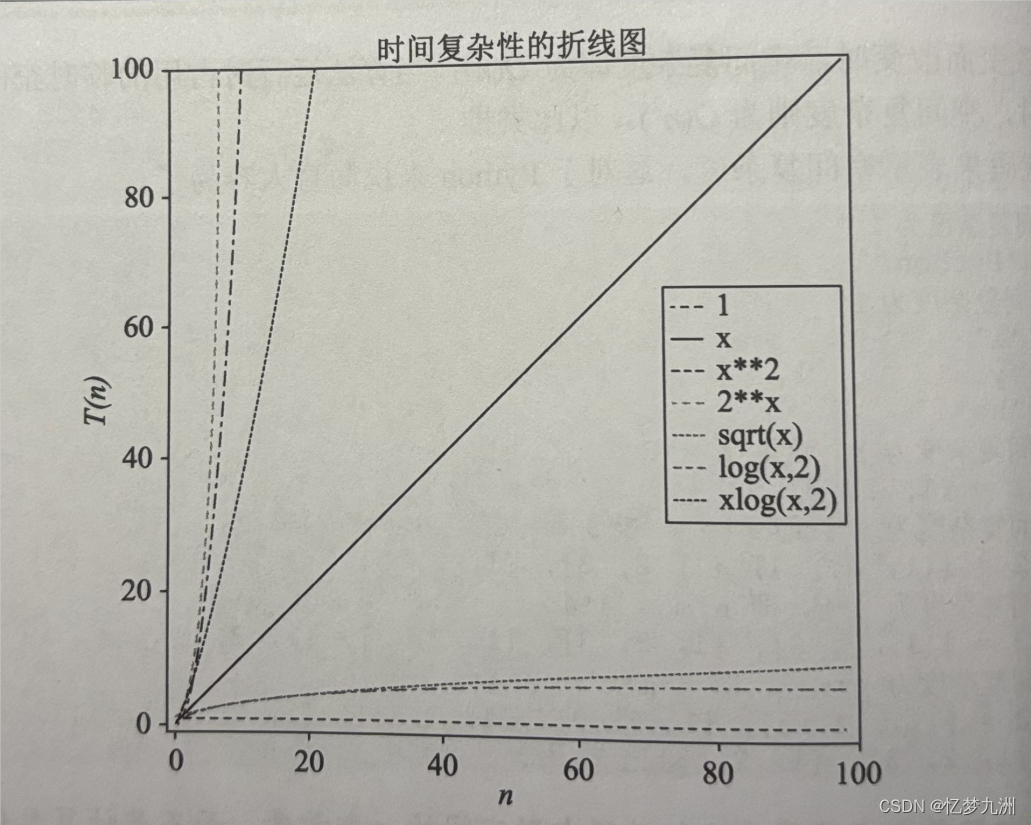 我们还能据此对算法进行分类。T(n)=O(1)类算法称作“常数时间算法”,T(n)=O(n)类算法称作“线性时间算法”,T(n)=
O
(
l
o
g
2
n
)
O(log_2n)
O(log2?n)类算法称作“对数时间算法”等。除此之外,还有幂对数时间算法、次线性时间算法和线性对数时间算法等。这些就交给大家自己去想去讨论,正好检验一下自己是否已经掌握。
我们还能据此对算法进行分类。T(n)=O(1)类算法称作“常数时间算法”,T(n)=O(n)类算法称作“线性时间算法”,T(n)=
O
(
l
o
g
2
n
)
O(log_2n)
O(log2?n)类算法称作“对数时间算法”等。除此之外,还有幂对数时间算法、次线性时间算法和线性对数时间算法等。这些就交给大家自己去想去讨论,正好检验一下自己是否已经掌握。
讲到这里还没有讲如何计算T(n)。不知道大家是否还记得空间复杂度的判别方法,如果不记得也没关系,毕竟T(n)和S(n)的计算完全不一样。
时间复杂度的计算方法
- 先将每行代码的执行次数写下来,然后相加。
- 将算式中的所有常数项去掉。
- 保留算式中的最高阶项。
- 去掉最高阶项的系数。
解读时间复杂度的计算方法
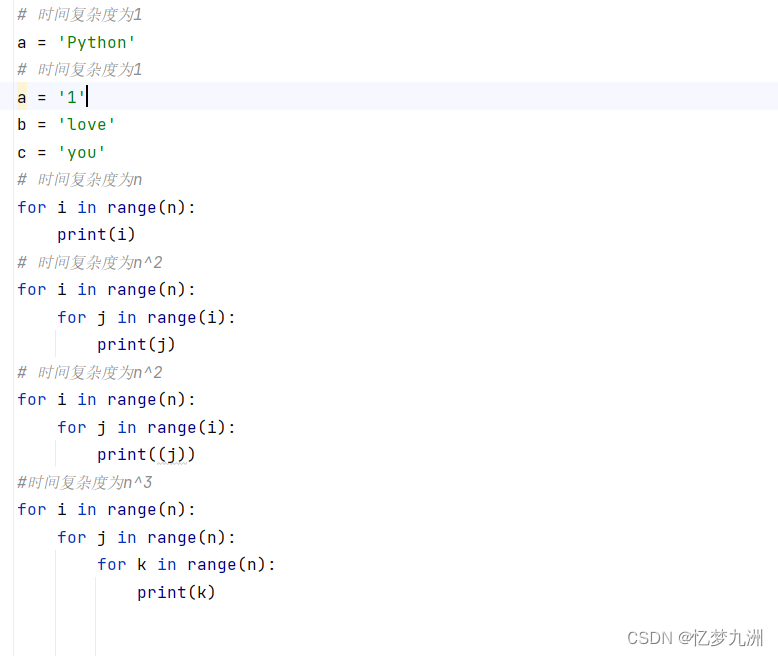
是不是没有看懂?笔者刚开始接触时间复杂度的时候也对其算法百思不解一脸懵逼,又是列式子又是一堆专业名词,差点被“绕晕”。不过,人生在勤,不索何获?在经过大量的练习和实际应用后,笔者终于参透并总结出了上面的时间复杂度的计算方法。和空间复杂度一样,用以下Python 代码来表示读者就能看明白了。
# 时间复杂度为1
a = 'Python'
# 时间复杂度为1
a = '1'
b = 'love'
c = 'you'
# 时间复杂度为n
for i in range(n):
print(i)
# 时间复杂度为n^2
for i in range(n):
for j in range(i):
print(j)
# 时间复杂度为n^2
for i in range(n):
for j in range(i):
print((j))
#时间复杂度为n^3
for i in range(n):
for j in range(n):
for k in range(n):
print(k)
注意
时间复杂度和空间复杂度一样,都只是算法运行时消耗时间的一个量度,而绝对
执行时间是无法计算的。
时间复杂度为 l o g n log_n logn?
是否觉得很简单 易如反掌?那就让我们继续学习下一个时间复杂度吧:
# 时间复杂度为(log n)
n = 64
while n >1 :
n = n // 2 #取商
print(n

运行结果

是否又觉得满腹疑团、如坠云雾?看,这段代码有一个 while 循环,而且每循环一次,n就要除以2然后取整,直到n不大于1。这个时候就应该想到log函数了,因这段代码和log函数的定义几乎一样。
因为
2
6
=
64
2^6=64
26=64
所以
l
o
g
2
64
=
l
o
g
2
2
6
=
6
log_2 64 = log_2 2^6=6
log2?64=log2?26=6
由此可见,答案就是
O
(
l
o
g
2
n
)
,
即
O
(
l
o
g
n
)
。
O(log_2 n),即O(logn)。
O(log2?n),即O(logn)。
由此我们可以得出结论:循环减半算法的时间复杂度为
O
(
l
o
g
2
n
)
O(log_2 n)
O(log2?n)
如果你实在理解不了这一段,那就记住结论吧。让我们继续看下一个时间复杂度
O
(
2
n
)
O(2^n)
O(2n)的代码:
# 时间复杂度为2^n
def fib0nacci(n):
# 当n为负数时
if n<0:
return 'invalid n' # 返回'invalid n'的错误提示
# 当n==0 和 n==1时
elif n<2:
return n #返回 n本身
return fib0nacci(n-1) +fib0nacci(n-2) #返回前两项的和
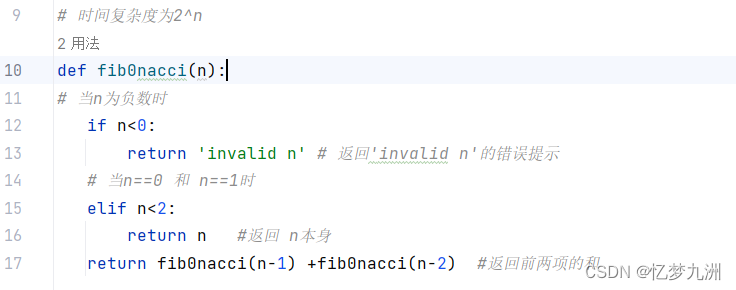
这是一个超级经典的算法,叫斐波那契数列,后面的文章还会讲到它,这里只是先让大家有个印象。由于上述代码使用了递归策略,所以它的时间复杂度是高度为(n-1)的不完全二叉树的节点数,近似为
O
(
n
2
)
O(n^2)
O(n2)。
注意
T(n) 是最坏情况复杂度。还有一种平均情况复杂度,一般在指定情况下使用。为了避免混淆,这里也不讲解,如果有兴趣可自行学习。
总结
了解了空间复杂度和时间复杂度之后,我们便可以据此对一个算法进行衡量。然而,所谓鱼和熊掌不可兼得,空间复杂度和时间复杂度也时常处在此消彼长的状况,这时候就需要我们选取一个平衡点,以达到最佳的效率。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 12V直流电机驱动芯片GC8837,兼容3.3V,5V逻辑输入
- 08-React路由(Router 6版本)
- YOLOv7-tiny,通过pycocotools包得到预测大中小尺寸目标的指标值
- 在访问一个网页时弹出的浏览器窗口,如何用selenium 网页自动化解决?
- 数据库插入数据
- 如何制作专业商业画册,提升品牌形象
- (1)(1.13) SiK无线电高级配置(六)
- RocketMQ5.0Pop消费模式
- 偶尔启动Idea2023版开发工具运行没有反应&&Idea都无法启动&&Idea双击无反应
- bash 功能脚本