【Coding】寒假每日一题Day.7.棋盘

题目来源

题目来自于AcWing平台：https://www.acwing.com/problem/content/description/5399/。
以blog的形式记录程序设计算法学习的过程，仅做学习记录之用。

题目描述+输入输出格式+数据范围

样例

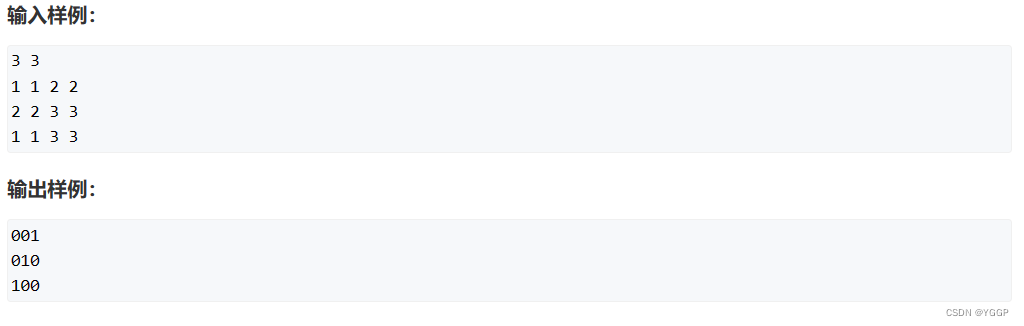
思路

思路参考自题解：https://www.acwing.com/solution/content/221556/

最开始拿到这道题的时候，实际上我已经看出来需要用前缀和&&差分来进行优化，但是有关前缀和与差分、二维前缀和与差分这一部分的模板我有点忘了，所以先使用了穷举法，看看能不能解决这道题。

在AcWing的OJ中，只过了前6个测试点，后4个测试点TLE了，因此去参看了题解回顾一下二维前缀和与差分的模板。

此处不记录二维前缀和与差分的模板是什么了，而直接记录为什么需要使用这两种方法。原因就在于，题目描述中说到，需要对$(x_1,y_1)$到$(x_2,y_2)$这一个区间内的数进行操作，自然想到可以使用前缀和与差分这两个高效的工具来对二维区间进行维护。

最后对于输出，如果操作次数是偶数，那么最后输出的是白棋，否则是黑棋。

Code

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int maxn = 2005;

int a[maxn][maxn] = {0};
int n, m;

int main()
{
    cin >> n >> m;
    for(int i=1;i<=m;i++){
        int x1, x2, y1, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        a[x2 + 1][y2 + 1] ++ ;
        a[x1][y1] ++ ;
        a[x2 + 1][y1] --;
        a[x1][y2 + 1] --;
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            a[i][j] += a[i-1][j] + a[i][j-1] - a[i-1][j-1];
        } 
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(a[i][j] % 2 == 0)    cout << 0;
            else                    cout << 1;
        }
        cout << endl;
    }
    return 0;
}