【每日一题】收集足够苹果的最小花园周长
Tag
【二分枚举答案】【二维网格】【2023-12-24】
题目来源
解题思路
方法一:二分枚举答案
思路
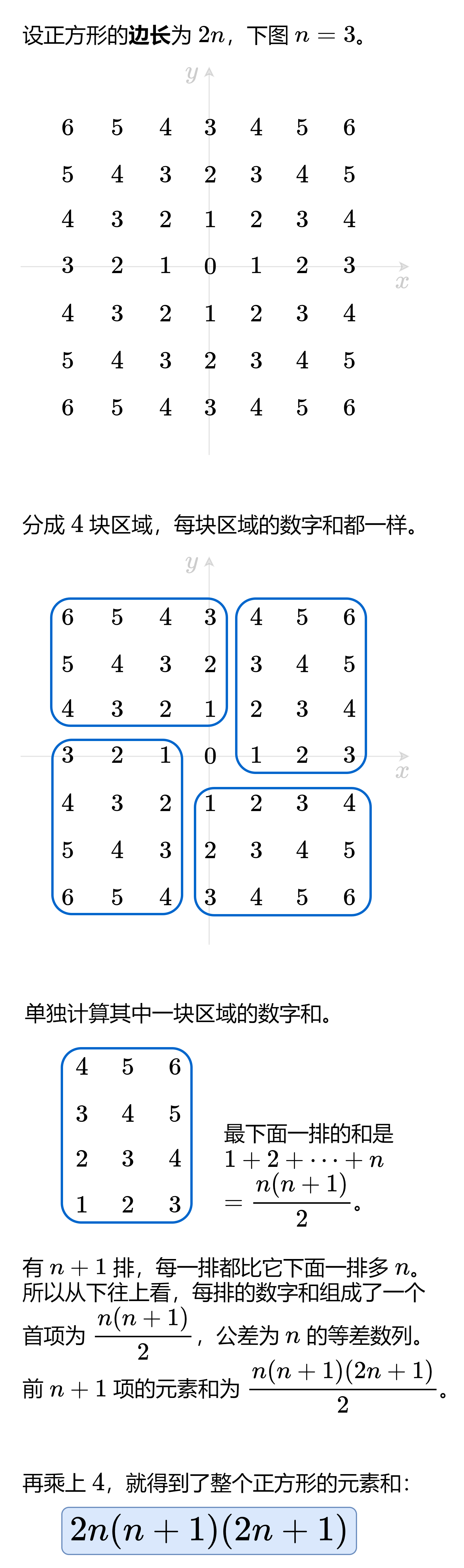
通过如下过程,我们可以求出边长为 2n 时,二维网格可以容纳的苹果数量为:
2 n ( n + 1 ) ( 2 n + 1 ) 2n(n+1)(2n+1) 2n(n+1)(2n+1)
图片来源 【图解】O(1) 做法(Python/Java/C++/Go/JS/Rust)。
随着边长的增大,二维网格可以容纳的苹果数量也在增大。于是我们可以二分枚举二维网格的边长,找出可以容纳 neededApples 个苹果的最小二维网格边长。
二分边界为 [1, 100000],其中 100000 是根据边长为 2n 的二维网格可以容纳苹果 2n(n+1)(2n+1) 估算得到。
算法
#define ll long long
class Solution {
public:
long long minimumPerimeter(long long neededApples) {
int l = 1, r = 100000;
int ans = 0;
while(l <= r){
int mid = (l + r) >> 1;
if((ll) 2*mid*(mid+1)*(2*mid+1) >= neededApples){
ans = mid;
r = mid - 1;
}
else{
l = mid + 1;
}
}
return ans * 8;
}
};
复杂度分析
时间复杂度: O ( l o g m ) O(logm) O(logm), m = n e e d e d A p p l e s 3 m = \sqrt[3]{neededApples} m=3neededApples?。
空间复杂度: O ( 1 ) O(1) O(1)。
写在最后
如果您发现文章有任何错误或者对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度的方法,欢迎评论区交流。
最后,感谢您的阅读,如果有所收获的话可以给我点一个 👍 哦。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Comdlg32.dll文件丢失怎么?Comdlg32.dll修复方法
- “| 型连续块”——岛屿数量BFS+递归解法
- 华为机试真题实战应用【赛题代码篇】-最小传输时延(附Java、C++和python代码)
- 有了AI Agents,RPA还有生存空间吗?
- PulsarServerException
- 正点原子imx6ull拷贝:通过SCP命令,实现Ubuntu和开发板拷贝
- 【无标题】
- 什么是残差矢量量化?
- 从今天起,你就是CAN专家了。
- TMC4671闭环调试步进、伺服、音圈、永磁、无刷电机