模拟生物自然进化的基因遗传算法
基因遗传算法(Genetic Algorithm,GA)是一种通过模拟生物进化过程来寻找最优解的优化算法。它是一种常见的启发式搜索算法,常用于优化、搜索和机器学习等领域。

生物基因遗传
生物的基因遗传是指父母通过基因传递给子代的过程。基因是DNA分子的一部分,它们携带着生物个体遗传信息的编码。每个生物个体都有两个拷贝的基因,一个来自母亲,另一个来自父亲。这些基因控制着生物个体的特征,如身高、眼睛颜色、皮肤颜色、血型等。
在基因遗传中,某些基因会表现为显性基因,而某些基因则表现为隐性基因。显性基因只需要一个基因拷贝就可以表现出来,而隐性基因需要两个基因拷贝才能表现出来。因此,如果一个生物个体有一个显性基因和一个隐性基因,那么它会表现出显性基因的特征。
基因遗传的机制是通过基因重组和基因突变实现的。基因重组是指在生殖细胞分裂过程中,母亲和父亲的基因随机组合,形成新的基因组合。基因突变是指在基因重组过程中,有可能出现突变,从而产生新的基因变异。这些基因变异可能会导致生物个体表现出新的特征或性状,或者增加或减少某些性状的发生率。
基因遗传是复杂而多样化的过程,它涉及基因重组、基因突变和其他多种因素。这些过程共同决定了生物个体的性状和遗传特征。
基因遗传算法通常由以下几个步骤组成:
- 初始化种群:随机生成一组初始解,称之为种群。种群中每个解由一组基因表示。
- 评估适应度:根据问题的优化目标,对每个解进行适应度评估。适应度越高,说明解越优。
- 选择:从种群中选择一些解,用于繁殖下一代。选择的方法可以是轮盘赌、竞争选择、锦标赛等。
- 交叉:将选择出的解进行交叉,产生新的解。交叉的方法可以是单点交叉、多点交叉、均匀交叉等。
- 变异:对新的解进行随机变异,产生更多的多样性。变异的方法可以是位变异、基因翻转等。
- 替换:用新的解替换掉旧的解,形成新的种群。
- 判断停止条件:判断算法是否满足停止条件,例如最大迭代次数、最大适应度等。
基因遗传算法通过不断地进行选择、交叉和变异来产生更好的解,最终收敛到一个或多个最优解。与其他优化算法相比,基因遗传算法具有以下优点:可以处理复杂的优化问题,具有并行化的能力,可以在不知道优化函数的具体形式时进行优化,适合处理具有多个局部最优解的问题等。
基因遗传算法是一种通过模拟自然进化过程来求解最优解的算法。其核心思想是将问题转换为一个优化问题,并使用基因编码、交叉、变异等操作来进行搜索。
生物基因遗传与基因遗传算法相关性对比
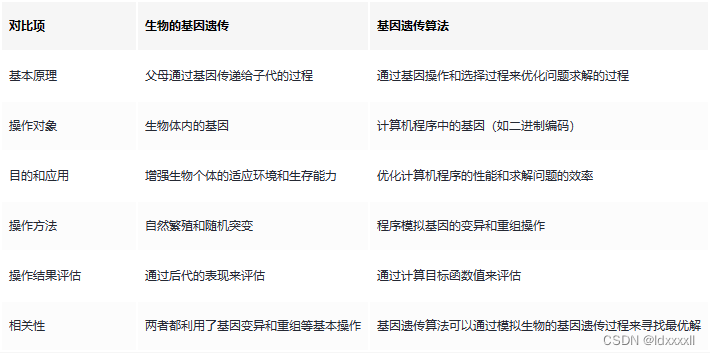
说明基因遗传算法基本流程的例子:
假设我们要求解以下函数的最大值:
f(x) = x^2 + 5x - 10
其中x的取值范围在[-10, 10]之间。我们可以将问题转换为求解f(x)的最大值,也就是找到x的最优解。下面是基因遗传算法的基本流程:
- 初始化种群 首先,我们需要初始化一个由多个个体组成的种群。每个个体都代表了一个可能的解,也就是x的一个取值。在本例中,我们可以随机生成一组x的取值作为初始种群,例如:
种群大小:10 个体1:x=2 个体2:x=-5 个体3:x=8 个体4:x=-3 个体5:x=1 个体6:x=-7 个体7:x=6 个体8:x=0 个体9:x=-2 个体10:x=10
- 评估适应度 接下来,我们需要评估每个个体的适应度,也就是计算它们的目标函数值。在本例中,我们可以将目标函数值定义为f(x),因此可以计算每个个体的适应度,例如:
个体1:f(2) = 2^2 + 5*2 - 10 = 4 + 10 - 10 = 4
个体2:f(-5) = (-5)^2 + 5*(-5) - 10 = 25 - 25 - 10 = -10
个体3:f(8) = 8^2 + 5*8 - 10 = 64 + 40 - 10 = 94
个体4:f(-3) = (-3)^2 + 5*(-3) - 10 = 9 - 15 - 10 = -16
个体5:f(1) = 1^2 + 5*1 - 10 = 1 + 5 - 10 = -4
个体6:f(-7) = (-7)^2 + 5*(-7) - 10 = 49 - 35 - 10 = 4
个体7:f(6) = 6^2 + 5*6 - 10 = 36 + 30 - 10 = 56
个体8:f(0) = 0^2 + 5*0 - 10 = -10
个体9:f(-2) = (-2)^2 + 5*(-2) - 10 = 4 - 10 - 10 = -16
个体10:f(10) = 10^2 + 5*10 - 10 = 100 + 50 - 10 = 140
- 选择操作 在选择操作中,我们需要根据每个个体的适应度选择一些优秀的个体用于下一代的繁殖。常见的选择算法有轮盘赌选择、锦标赛选择等。
- 以轮盘赌选择为例,选择个体的概率与其适应度成正比。我们可以按照以下步骤进行轮盘赌选择:
- 计算适应度总和S=sum(fitness_i),其中fitness_i为第i个个体的适应度。
- 对于每个个体i,计算其选择概率p_i=fitness_i/S。
生成一个[0,1)之间的随机数r,选择第一个满足sum(p_1~p_j)>r的个体j。
例如,对于上面的例子,我们可以计算适应度总和为:
S = 4 + (-10) + 94 + (-16) + (-4) + 4 + 56 + (-10) + (-16) + 140 = 126。
然后,我们可以计算每个个体的选择概率,例如个体1的选择概率为:p_1 = 4/126 ≈ 0.032。接着,我们可以生成一个随机数r,例如 r=0.3。然后,我们从个体1开始累加选择概率,当累加和大于等于r时,停止累加,选择当前个体,例如选择个体4(x=-3)作为父代。
- 交叉操作 在交叉操作中,我们随机选择两个父代进行交叉,生成两个新的后代。具体来说,我们可以选择一个交叉点,将两个父代的基因分别交换,生成两个新的后代。例如,假设选择父代1(x=2)和父代4(x=-3)进行交叉,选择交叉点为x=0,我们可以得到两个新的后代:
后代1:x=2(来自父代1),x=-3(来自父代4),因此x=2和x=-3进行了交叉操作。 后代2:x=-3(来自父代4),x=2(来自父代1),因此x=-3和x=2进行了交叉操作。
- 变异操作 在变异操作中,我们随机选择一些后代进行变异,生成一些新的个体。具体来说,我们可以随机选择一个后代,将其某个基因进行随机变化。例如,假设选择后代1进行变异,随机选择一个位置进行变异,例如将x=2变为x=3,得到一个新的个体:
个体11:x=3
- 更新种群 最后,我们需要将新生成的个体加入到种群中,并用一些选择算法选择出下一代的父代。然后重复上述操作,直到达到终止条件。
终止条件:
在遗传算法中,我们需要设定一些终止条件,以控制算法的运行时间和结果质量。常见的终止条件包括:
- 达到最大迭代次数
- 达到最大运行时间
- 达到目标函数的阈值
- 所有个体的适应度趋于稳定不再变化
例如,我们可以设定最大迭代次数为1000,如果达到了最大迭代次数,算法就会停止并输出最优解。
可以看到,基因遗传算法是一种通过模拟自然选择和遗传机制来搜索最优解的算法。它具有全局搜索能力、并行计算能力和鲁棒性等优点。
基因遗传算法可以应用于许多实际问题的优化和搜索
一些基因遗传算法的应用场景的例子:
- 旅行商问题(TSP) 旅行商问题是一个经典的组合优化问题,目的是在许多城市之间寻找最短的路径。基因遗传算法可以用于寻找最优解,即访问所有城市的最短路径。
- 排队论 排队论是研究服务系统如何组织和管理的一种数学方法。基因遗传算法可以应用于优化排队论中的各种指标,如等待时间、服务时间等。
- 机器学习特征选择 在机器学习中,特征选择是一个重要的问题。基因遗传算法可以应用于特征选择,从而提高模型的性能和可解释性。
- 信号处理 在信号处理中,基因遗传算法可以应用于优化信号的滤波器设计、信号分类、降噪等问题。
- 电力系统优化 在电力系统中,基因遗传算法可以应用于优化电网的输电线路、容量配置、电压稳定性等问题。
- 股票投资 在股票投资中,基因遗传算法可以应用于优化投资组合的配置、预测股票价格等问题。
- 网络优化 在网络优化中,基因遗传算法可以应用于路由优化、网络拓扑设计、网络容量规划等问题。
- 航空航天优化 在航空航天领域中,基因遗传算法可以应用于优化飞机或火箭的设计、航线规划等问题。
基因遗传算法是一种通用的优化算法,可以应用于各种领域的问题。只要问题可以转化为寻找最优解的形式,基因遗传算法就可能是一个可行的解决方案。
优化算法解释:
优化算法是指一类被设计用于求解最优化问题的算法。最优化问题的目标是在给定的约束条件下,找到使得目标函数达到最小值或最大值的一组参数或变量。
优化算法可以应用于各种领域,例如工程设计、经济学、金融学、机器学习、神经网络等。常见的优化算法包括梯度下降法、牛顿法、拟牛顿法、共轭梯度法、遗传算法、模拟退火算法等。
这些算法的选择取决于具体问题的特性,例如目标函数的形式、约束条件的数量和复杂度、计算资源的可用性等。通过选择合适的优化算法,可以有效地求解最优化问题,并得到理想的结果。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 111练手项目
- Java 说一下乐观锁和悲观锁?
- AI短视频生成与制作从入门到精通
- 为什么Certum旗下的多域名证书会过期
- 数据采集有哪些方法?HTTP代理起到什么作用?
- Vue改变数据,页面不刷新的问题
- UniversalTransformer with Adaptive Computation Time(ACT)
- 公开100GB数据,日产汽车遭勒索组织“撕票”
- 为什么选择在线解析网站来做视频提取?了解更多详情!
- 在vue中如何实现准时的setTimeout