一些常用的距离

说明
以下是一些常用的距离度量及其使用说明和应用场景，不仅在图像、文本检测中有应用，像A*算法的启发式函数，也会用到它们，感觉挺有意思的：

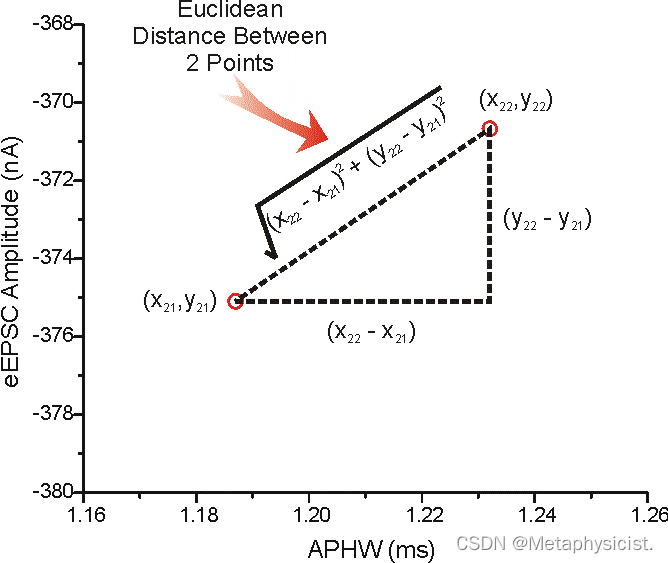
欧氏距离（Euclidean Distance）：欧氏距离是最常用的距离度量，用于衡量两个向量之间的几何距离。它可以用于图像检索、目标识别和图像聚类等任务。得名于欧几里得,是古希腊数学家,他最早提出了用两点间的直线距离来衡量它们在平面坐标系中的间隔。
$$d(\mathbf{x},\mathbf{y})=\sqrt{\sum _{i=1}^n(x_i?y_i{)}^2}$$

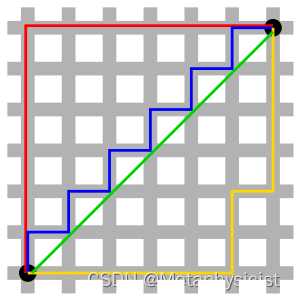
曼哈顿距离（Manhattan Distance）：曼哈顿距离是指两个向量之间的每个维度差的绝对值之和。它适用于特征具有明显方向性的情况，例如图像中的轮廓特征。得名于曼哈顿区的城市布局,两个坐标差的绝对值就像在曼哈顿区从一个街区走到另一个街区那样的距离总和。
$$d(\mathbf{x},\mathbf{y})=\sum _{i=1}^n\left|x_i?y_i\right|$$

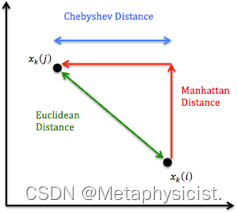
切比雪夫距离（Chebyshev Distance）：切比雪夫距离是指两个向量之间的最大维度差。它适用于特征具有明显方向性的情况，例如图像中的边缘特征。得名于19世纪俄国数学家帕夫诺维奇·切比雪夫。它考虑特征空间中最大轴向距离,适用于边缘检测等需要关注局部最大差异的场景。
$$d(\mathbf{x},\mathbf{y})=\max i\left|xi?y_i\right|$$

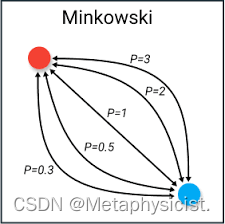
闵可夫斯基距离（Minkowski Distance）：闵可夫斯基距离是欧氏距离和曼哈顿距离的一种推广，可以通过调整参数p来控制距离的形状。当p=1时，闵可夫斯基距离等同于曼哈顿距离；当p=2时，闵可夫斯基距离等同于欧氏距离。得名于苏联数学家列昂尼得·闵可夫斯基,是欧式和曼哈顿距离的广义形式。
$$d(\mathbf{x},\mathbf{y})={\left(\sum _{i=1}^n|x_i?y_i{|}^p\right)}^{\frac{1}{p}}$$

余弦相似度（Cosine Similarity）：余弦相似度衡量两个向量之间的夹角余弦值，用于衡量向量之间的相似性。它常用于文本分类和图像检索等任务。
$$Sim(\mathbf{x},\mathbf{y})=\frac{\mathbf{x}?\mathbf{y}}{|\mathbf{x}||\mathbf{y}|}$$
汉明距离（Hamming Distance）：汉明距离用于衡量两个等长字符串之间的不同位数。在图像处理中，汉明距离可以用于衡量两个二值图像之间的不同位数。得名于克劳德·伊万斯·汉明,它直接计算两个等长字符串在对应位置不同字符的数量,适用于错误检测等应用。
$$d(x,y)=\text{?number?of?positions?where?}x\text{?and?}y\text{?differ?}$$

这些距离度量方法在图像处理中有广泛的应用，例如图像检索和相似图像聚类。根据具体的任务和特征，选择适合的距离度量方法可以提高算法的性能和准确性。

import numpy as np

# 欧式距离
def euclidean_distance(x, y):
    return np.linalg.norm(x - y)

# 曼哈顿距离 
def manhattan_distance(x, y):
    return np.sum(np.abs(x - y))

# 切比雪夫距离
def chebyshev_distance(x, y):
    return np.max(np.abs(x - y))

# 闵可夫斯基距离
def minkowski_distance(x, y, p=2):
    return np.linalg.norm(x - y, p)

# 余弦相似度  
def cosine_similarity(x, y):
    return np.dot(x, y) / (np.linalg.norm(x) * np.linalg.norm(y))

# 测试
x = np.array([1, 2, 3])
y = np.array([4, 5, 6])

print('Euclidean distance: ', euclidean_distance(x, y))
print('Manhattan distance: ', manhattan_distance(x, y)) 
print('Chebyshev distance: ', chebyshev_distance(x, y))
print('Minkowski distance: ', minkowski_distance(x, y))
print('Cosine similarity: ', cosine_similarity(x, y))

% 欧式距离
function d = euclideanDistance(x, y)
   d = norm(x - y); 
end

% 曼哈顿距离
function d = manhattanDistance(x, y)
   d = sum(abs(x - y));
end

% 切比雪夫距离 
function d = chebyshevDistance(x, y)
   d = max(abs(x - y));
end

% 闵可夫斯基距离
function d = minkowskiDistance(x, y, p)
   d = norm(x - y, p);  
end

% 余弦相似度
function s = cosineSimilarity(x, y)
   s = sum(x.*y)/(norm(x)*norm(y));
end

% 测试
x = [1 2 3];
y = [4 5 6];

fprintf('Euclidean distance: %f\n', euclideanDistance(x,y))
fprintf('Manhattan distance: %f\n', manhattanDistance(x,y))
fprintf('Chebyshev distance: %f\n', chebyshevDistance(x,y)) 
fprintf('Minkowski distance: %f\n', minkowskiDistance(x,y,2))
fprintf('Cosine similarity: %f\n', cosineSimilarity(x,y))