第4章 | 安徽某高校《统计建模与R软件》期末复习
第4章? 参数估计
参数估计是统计建模的关键步骤之一,它涉及根据样本数据推断总体参数的过程。在统计学中,参数通常用于描述总体的特征,如均值、方差等。通过参数估计,我们可以利用样本信息对这些未知参数进行推断,从而对总体进行更深入的了解。
4.1 矩法?
思想:当我们面对一个统计问题时,通常我们不能观察到整个总体的所有数据,而只能通过取一部分样本来进行研究。为了从这个样本中了解总体的性质,我们引入了一种思想,即使用样本的一些数字特征(矩)来估计总体相应的特征。在这个过程中,我们关注的是总体的矩,而这些矩与总体的参数有密切的关系,从而允许我们得出对总体参数的估计。
矩是描述数据分布的一种方式,例如均值和方差就是常见的矩。我们可以通过样本计算得到样本的矩,然后利用这些样本矩去估计总体的矩,进而得到总体参数的估计。
比如,如果我们想知道一个总体的平均值是多少,我们可以从样本中计算出样本均值,然后用样本均值去估计总体的平均值。这是因为,根据统计理论,样本均值与总体均值有一个紧密的关系,特别是在样本容量足够大的情况下。
这种思想的优势在于,通过研究样本矩与总体矩之间的关系,我们可以从有限的样本中获取关于总体特征的有用信息,而不必观察整个总体。这为我们提供了一种有效的方式,通过小规模的样本来推断和估计总体的性质。
4.1.1 矩法
矩法是一种矩估计法。矩法的核心思想是使用样本矩(样本的各阶矩)去估计总体矩,从而得到总体参数的估计。样本??阶矩的公式如下:
其中:
- n 是样本容量,表示样本中的观测值个数。
?是第?
?个观测值。
?是矩的阶数,表示对观测值取?
?次幂。
举例:设总体的分布函数中有m个未知参数,假设总体样本的?
?阶原点矩存在,样本?
?,令总体的
?阶原点矩等于样本的?
?阶原点矩。以一阶、二阶矩法估计参数举例:
我们可以解得均值和方差的矩法估计:
4.1.2 R语言实现
在二项分布B(k;p)中,求k和p的矩估计。
1)一阶二阶矩法
为样本均值:
为样本二阶中心矩:
解得:?,?
# 模拟二项分布
# N=20,p=0.7,试验次数n=100
x <- rbinom(100, 20, 0.7)
# 计算样本均值
m1 <- mean(x)
# 计算样本方差
m2 <- sum((x - mean(x))^2) / 100
# 计算 N
N <- m1^2 / (m1 - m2)
# 计算 p
p <- (m1 - m2) / m12)Newton-Raphson 方法的矩估计
# 定义矩估计函数
moment_fun <- function(p) {
# 计算方程组
f <- c(p[1] * p[2] - M1, p[1] * p[2] - p[1] * p[2]^2 - M2)
# 计算雅可比矩阵
J <- matrix(c(p[2], p[1], p[2] - p[2]^2, p[1] - 2 * p[1] * p[2]), nrow = 2, byrow = TRUE)
list(f = f, J = J)
}
# 定义 Newton-Raphson 优化函数
Newtons <- function(fun, x, ep = 1e-5, it_max = 100) {
index <- 0
k <- 1
while (k <= it_max) {
x1 <- x
obj <- fun(x)
x <- x - solve(obj$J, obj$f)
norm <- sqrt(sum((x - x1)^2))
if (norm < ep) {
index <- 1
break
}
k <- k + 1
}
obj <- fun(x)
list(root = x, it = k, index = index, FunVal = obj$f)
}
# 生成二项分布样本
x <- rbinom(100, 20, 0.7)
# 获取样本大小
n <- length(x)
# 计算样本均值和样本方差
M1 <- mean(x)
M2 <- (n - 1) / n * var(x)
# 初始猜测值
p <- c(10, 0.5)
# 使用 Newton-Raphson 优化估计参数
result <- Newtons(moment_fun, p)
# 输出估计的参数值和迭代次数
cat("估计的 n:", result$root[1], "\n")
cat("估计的 p:", result$root[2], "\n")
cat("迭代次数:", result$it, "\n")4.2 极大似然法
4.2.1 极大似然估计
极大似然估计是一种用于估计统计模型参数的方法。它基于观测到的样本数据,试图找到使得观测数据出现的概率最大的参数值。在讲解极大似然估计之前,我们先来了解一下一些基本的概念。
1)似然函数
似然函数是一个关于模型参数的函数,它描述了在给定模型下观测数据的可能性。对于参数为θ的模型,给定观测到的数据集X,似然函数表示为 L(θ|X)。对于离散型随机变量,似然函数通常是概率质量函数的乘积;对于连续型随机变量,似然函数是概率密度函数的乘积。
设总体X的概率密度函数或分布律为,?
是来自总体X的样本,则
的似然函数为:
2)极大似然估计
极大似然估计的目标是找到使似然函数取最大值的参数值,即找到使得观测到的数据在给定模型下出现的概率最大的模型参数。通常我们会取对数似然函数,因为这样便于计算。
假设有一组观测数据X={x?, x?, ..., x?},且这些数据是从一个分布(比如正态分布、二项分布等)中产生的。该分布有一个参数θ,我们的目标是通过这组观测数据估计出θ。
-
写出似然函数: 建立观测数据的似然函数L(θ|X),表示观测数据在给定参数θ下的概率。
-
取对数: 通常取对数似然函数,因为对数函数的最大值点与原函数的最大值点是一样的,而且对数函数便于计算。
-
求导数: 对对数似然函数关于θ的导数,然后令导数等于零,解出参数θ。
-
解方程: 解出的θ值即为极大似然估计。
4.2.2 R语言实现
1) ?连续
?连续
举例:正态分布
# 安装并加载 rootSolve 包
# install.packages("rootSolve") # 如果未安装,需要先运行这行代码安装包
library(rootSolve)
# 生成样本
x <- rnorm(10)
# 定义似然函数和 multiroot 求解模型
model <- function(e, x) {
n <- length(x)
F1 <- sum(x - e[1])
F2 <- -n / (e[2])^2 + sum((x - e[1])^2) / e[2]^4
c(F1, F2)
}
# 使用 multiroot 函数计算似然方程组的根(即估计的参数)
result <- multiroot(f = model, start = c(0, 1), x = x)
# 输出结果
cat("估计的均值:", result$root[1], "\n")
cat("估计的标准差:", result$root[2], "\n")
4) ?离散
?离散
# 生成 Cauchy 分布的样本
x <- rcauchy(100, 1)
# 定义对数似然函数
loglike <- function(p) {
n <- length(x)
log(3.14159) * n + sum(log(1 + (x - p)^2))
}
# 使用 optimize 函数找到对数似然函数的最大值
result <- optimize(loglike, interval = c(0, 5))
# 输出结果
cat("估计的参数 p:", result$maximum, "\n")
cat("对数似然函数的最大值:", result$objective, "\n")
4.3 区间估计
4.3.1 区间估计
设总体X的分布函数F(x,θ)含有未知参数θ,对于给定值α(0< α<1),若由样本确定的两个统计量,
和
满足:
则称随机区间是参数
的置信度为
的置信区间。
4.3.2 一个正态总体的区间估计
1)均值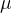 的估计
的估计
已知时:参数
的置信度为
的双侧置信区间:
? ? ? ? 推出:
未知时:参数
的置信度为
的双侧置信区间:
? ? ? ? 推出:
在R语言中,我们可以引入interval_esitimate11函数来做估计:
# 定义函数 interval_estimate11
# 参数:
# x: 数据向量
# sigma: 总体标准差,如果为正值则使用,否则使用样本标准差
# alpha: 置信水平,默认为 0.05
interval_estimate11 <- function(x, sigma = -1, alpha = 0.05) {
n <- length(x)
xb <- mean(x)
# 根据 sigma 是否为正值选择使用 Z 分布或者 t 分布
if (sigma >= 0) {
tmp <- sigma / sqrt(n) * qnorm(1 - alpha / 2) # Z 分布的临界值
df <- n
} else {
# 当 sigma 为负值时,根据样本大小选择使用 Z 分布或者 t 分布
if (n >= 30) {
tmp <- sd(x) / sqrt(n) * qnorm(1 - alpha / 2) # Z 分布的临界值
df <- n
} else {
tmp <- sd(x) / sqrt(n) * qt(1 - alpha / 2, n - 1) # t 分布的临界值
df <- n - 1
}
}
# 构建结果数据框
result <- data.frame(mean = xb, df = df, a = xb - tmp, b = xb + tmp)
return(result)
}
# 生成样本数据
x <- rnorm(20, 1, 0.04)
# 调用函数并输出结果
interval_estimate11(x)在R语言中,函数 t.test() 也提供了 t 检验和相应的区间估计的功能:
t.test(x, # 第一个样本或一组观测值
y = NULL, # 第二个样本,如果只有一个样本则为 NULL
alternative = c("two.sided", "less", "greater"),
# 假设检验的方向,可选值为 "two.sided"(双侧检验,默认)、"less"(左侧检验)、"greater"(右侧检验)
mu = 0, # 要检验的假设均值,默认为 0
paired = FALSE, # 是否为配对样本(paired samples),默认为 FALSE
var.equal = FALSE, # 是否假设两个总体方差相等,默认为 FALSE
conf.level = 0.95) # 置信水平,默认为 0.95
2)方差 的估计
的估计
已知时:参数
的置信度为
的双侧置信区间:
未知时:参数
的置信度为
的双侧置信区间:
在R语言中,我们可以引入函数interval_var1来求解:
# 定义函数 interval_var1
# 参数:
# x: 数据向量
# mu: 假设的总体方差值,默认为 Inf 表示不指定
# alpha: 置信水平,默认为 0.05
interval_var1 <- function(x, mu = Inf, alpha = 0.05) {
n <- length(x)
# 根据 mu 是否为无穷选择使用总体方差估计还是样本方差估计
if (mu < Inf) {
S2 <- sum((x - mu)^2) / n
df <- n
} else {
S2 <- var(x)
df <- n - 1
}
# 计算置信区间的上下界
a <- df * S2 / qchisq(1 - alpha / 2, df)
b <- df * S2 / qchisq(alpha / 2, df)
# 构建结果数据框
result <- data.frame(var = S2, df = df, a = a, b = b)
return(result)
}
# 生成样本数据
x <- c(23, 25, 28, 22, 20)
# 调用函数并输出结果
interval_var1(x)
4.3.3 两个正态总体的区间估计
解决两个正态总体的区间估计时,我们可以引入函数interval_estimate2:
# 定义函数 interval_estimate2
# 参数:
# x: 第一个样本数据向量
# y: 第二个样本数据向量
# sigma: 总体标准差,如果为正值则使用,否则使用样本标准差
# var.equal: 是否假设两个总体方差相等,默认为 FALSE
# alpha: 置信水平,默认为 0.05
interval_estimate2 <- function(x, y, sigma = c(-1, -1), var.equal = FALSE, alpha = 0.05) {
n1 <- length(x)
n2 <- length(y)
xb <- mean(x)
yb <- mean(y)
if (all(sigma >= 0)) { # 均值差μ1- μ2的区间估计(置信度为1-α)
tmp <- qnorm(1 - alpha / 2) * sqrt(sigma[1]^2 / n1 + sigma[2]^2 / n2)
df <- n1 + n2
} else {
if (var.equal == TRUE) {
Sw <- ((n1 - 1) * var(x) + (n2 - 1) * var(y)) / (n1 + n2 - 2)
tmp <- sqrt(Sw * (1 / n1 + 1 / n2)) * qt(1 - alpha / 2, n1 + n2 - 2)
df <- n1 + n2 - 2
} else {
S1 <- var(x)
S2 <- var(y)
nu <- (S1 / n1 + S2 / n2)^2 / (S1 / n1^2 / (n1 - 1) + S2 / n2^2 / (n2 - 1))
tmp <- qt(1 - alpha / 2, nu) * sqrt(S1 / n1 + S2 / n2)
df <- nu
}
}
# 构建结果数据框
result <- data.frame(mean = xb - yb, df = df, a = xb - yb - tmp, b = xb - yb + tmp)
return(result)
}
# 生成两个样本数据
x <- c(23, 25, 28, 22, 20)
y <- c(29, 31, 30, 32, 27)
# 调用函数并输出结果
interval_estimate2(x, y)
4.3.4 配对数据均值差的区间估计
我们可以用 t.test() 函数直接求解:
# 定义两组观测值
x <- c(11.3, 15.0, 15.0, 13.5, 12.8, 10.0, 11.0, 12.0, 13.0, 12.3)
y <- c(14.0, 13.8, 14.0, 13.5, 13.5, 12.0, 14.7, 11.4, 13.8, 12.0)
# 执行独立样本 t 检验
result <- t.test(x - y)
# 输出检验结果
print(result)
也可以引入前面的interval_estimate1函数:
# 定义函数 interval_estimate1
# 参数:
# x: 数据向量
# mu: 假设的总体均值,默认为 Inf 表示不指定
# alpha: 置信水平,默认为 0.05
interval_estimate1 <- function(x, mu = Inf, alpha = 0.05) {
n <- length(x)
# 根据 mu 是否为无穷选择使用总体均值估计还是样本均值估计
if (mu < Inf) {
mean_val <- mu
tmp <- qnorm(1 - alpha / 2) * sqrt(var(x) / n)
df <- n
} else {
mean_val <- mean(x)
tmp <- qt(1 - alpha / 2, df = n - 1) * sqrt(var(x) / n)
df <- n - 1
}
# 计算置信区间的上下界
a <- mean_val - tmp
b <- mean_val + tmp
# 构建结果数据框
result <- data.frame(mean = mean_val, df = df, a = a, b = b)
return(result)
}
# 定义两组观测值
x <- c(11.3, 15.0, 15.0, 13.5, 12.8, 10.0, 11.0, 12.0, 13.0, 12.3)
y <- c(14.0, 13.8, 14.0, 13.5, 13.5, 12.0, 14.7, 11.4, 13.8, 12.0)
# 计算差异向量
z <- x - y
# 调用函数并输出结果
interval_estimate1(z)4.3.5 方差比的区间估计
# 定义函数 interval_var2
# 参数:
# x: 第一个样本数据向量
# y: 第二个样本数据向量
# mu: 假设的总体方差比率,默认为 Inf 表示不指定
# alpha: 置信水平,默认为 0.05
interval_var2 <- function(x, y, mu = c(Inf, Inf), alpha = 0.05) {
n1 <- length(x)
n2 <- length(y)
if (all(mu < Inf)) {
Sx2 <- 1 / n1 * sum((x - mu[1])^2)
Sy2 <- 1 / n2 * sum((y - mu[2])^2)
df1 <- n1
df2 <- n2
} else if (mu[1] < Inf && mu[2] == Inf) {
Sx2 <- 1 / n1 * sum((x - mu[1])^2)
Sy2 <- var(y)
df1 <- n1
df2 <- n2 - 1
} else if (mu[1] == Inf && mu[2] < Inf) {
Sx2 <- var(x)
Sy2 <- 1 / n2 * sum((y - mu[2])^2)
df1 <- n1 - 1
df2 <- n2
} else {
Sx2 <- var(x)
Sy2 <- var(y)
df1 <- n1 - 1
df2 <- n2 - 1
}
r <- Sx2 / Sy2
a <- r / qf(1 - alpha / 2, df1, df2)
b <- r / qf(alpha / 2, df1, df2)
# 构建结果数据框
result <- data.frame(rate = r, df1 = df1, df2 = df2, a = a, b = b)
return(result)
}
# 定义两组观测值
a <- c(79.98, 80.04, 80.02, 80.04, 80.03, 80.03, 80.04, 79.97, 80.05, 80.03, 80.02, 80.00, 80.02)
b <- c(80.02, 79.94, 79.98, 79.97, 79.97, 80.03, 79.95, 79.97)
# 调用函数并输出结果
interval_var2(a, b, mu = c(80, 60))
interval_var2(a, b, mu = c(Inf, Inf))
interval_var2(a, b, mu = c(80, Inf))
interval_var2(a, b, mu = c(Inf, 60))
4.3.6 非正态总体的区间估计
# 定义函数 interval_estimate3
# 参数:
# x: 数据向量
# sigma: 总体标准差的估计值,默认为 -1,表示使用样本标准差
# alpha: 置信水平,默认为 0.05
interval_estimate3 <- function(x, sigma = -1, alpha = 0.05) {
n <- length(x)
xb <- mean(x)
if (sigma >= 0) {
tmp <- sigma / sqrt(n) * qnorm(1 - alpha / 2)
} else {
tmp <- sd(x) / sqrt(n) * qnorm(1 - alpha / 2)
}
# 构建结果数据框
result <- data.frame(mean = xb, a = xb - tmp, b = xb + tmp)
return(result)
}
# 使用示例:
# 定义一个数据向量
x <- c(11.3, 15.0, 15.0, 13.5, 12.8, 10.0, 11.0, 12.0, 13.0, 12.3)
# 调用函数并输出结果
interval_estimate3(x)4.3.7 单侧置信区间估计
# 定义函数 interval_estimate4
# 参数:
# x: 数据向量
# sigma: 总体标准差的估计值,默认为 -1,表示使用样本标准差
# side: 置信区间的一侧,默认为 0 表示双侧置信区间,<0 表示左侧,>0 表示右侧
# alpha: 置信水平,默认为 0.05
interval_estimate4 <- function(x, sigma = -1, side = 0, alpha = 0.05) {
n <- length(x)
xb <- mean(x)
if (sigma >= 0) { # 总体标准差已知
if (side < 0) { # 左侧置信区间
tmp <- sigma / sqrt(n) * qnorm(1 - alpha)
a <- -Inf
b <- xb + tmp
} else if (side > 0) { # 右侧置信区间
tmp <- sigma / sqrt(n) * qnorm(1 - alpha)
a <- xb - tmp
b <- Inf
} else { # 双侧置信区间
tmp <- sigma / sqrt(n) * qnorm(1 - alpha / 2)
a <- xb - tmp
b <- xb + tmp
}
df <- n
} else { # 总体标准差未知
if (side < 0) { # 左侧置信区间
tmp <- sd(x) / sqrt(n) * qt(1 - alpha, n - 1)
a <- -Inf
b <- xb + tmp
} else if (side > 0) { # 右侧置信区间
tmp <- sd(x) / sqrt(n) * qt(1 - alpha, n - 1)
a <- xb - tmp
b <- Inf
} else { # 双侧置信区间
tmp <- sd(x) / sqrt(n) * qt(1 - alpha / 2, n - 1)
a <- xb - tmp
b <- xb + tmp
}
df <- n - 1
}
# 构建结果数据框
result <- data.frame(mean = xb, df = df, a = a, b = b)
return(result)
}
# 使用示例:
# 定义一个数据向量
x <- c(11.3, 15.0, 15.0, 13.5, 12.8, 10.0, 11.0, 12.0, 13.0, 12.3)
# 调用函数并输出结果
# 默认为双侧置信区间
interval_estimate4(x)
# 左侧置信区间
interval_estimate4(x, side = -1)
# 右侧置信区间
interval_estimate4(x, side = 1)
(个人总结,如有谬误或需要改进之处欢迎联系作者)
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【论文精读】A Survey on Large Language Model based Autonomous Agents
- “MapStruct妙用指南:解锁Java对象映射的强大力量!“ ?
- Go语言中的乐观锁与悲观锁
- shell 如何调用多个脚本
- 反向代理的本质是什么?
- Pandas实战100例 | 案例 51: 日期时间过滤
- 【C语言】TCP测速程序
- Python陷阱-如何安全地删除列表元素?
- 司铭宇老师:房地产中介电话销售培训:房地产中介电话销售技巧
- 基于Java SSM框架实现医院病历管理系统项目【项目源码+论文说明】计算机毕业设计