EXPLORING DIFFUSION MODELS FOR UNSUPERVISED VIDEO ANOMALY DETECTION 论文阅读
EXPLORING DIFFUSION MODELS FOR UNSUPERVISED VIDEO ANOMALY DETECTION 论文阅读
论文标题:EXPLORING DIFFUSION MODELS FOR UNSUPERVISED VIDEO ANOMALY DETECTION
文章信息:

发表于:ICIP 2023
原文链接:https://arxiv.org/abs/2304.05841
源码:https://github.com/AnilOsmanTur/video_anomaly_diffusion
ABSTRACT
这篇论文调查了扩散模型在视频异常检测(VAD)中的性能,特别关注最具挑战性但也是最实际的场景,即在没有使用数据注释的情况下进行检测。由于数据往往是稀疏、多样化、具有上下文并且常常含糊不清,精确检测异常事件是一项非常雄心勃勃的任务。为此,我们仅依赖于信息丰富的时空数据和扩散模型的重建能力,通过高重建误差来判断异常性。在两个大规模视频异常检测数据集上进行的实验证明了所提方法相对于最先进的生成模型的一致改进,而在某些情况下,我们的方法得分甚至优于更复杂的模型。这是第一项使用扩散模型并研究其参数影响的研究,为监控场景中的VAD提供了指导。
1. INTRODUCTION
由于视频数量呈指数级增长,自动化视频异常检测(VAD)已成为计算机视觉领域中的一项关键任务。VAD与智能监控和行为理解等多个应用密切相关[1, 2, 3, 4, 5, 6]。异常通常被定义为一种罕见、意外或不寻常的实体,其与正常性显著偏离,而正常性被定义为预期和普遍的状态。尽管异常事件往往是稀疏且多样化的,但它们也具有很强的上下文性,并且常常具有歧义性,因此这些特点对VAD模型的性能构成了挑战[7]。
数据标注已经是一个臭名昭著的昂贵和耗时的任务,考虑到异常事件的前述特征,几乎不可能收集所有可能的异常样本来执行完全监督学习方法。因此,在VAD中,一个典型的方法是训练一个单类别分类器,该分类器从正常的训练数据中学习[8, 9, 10]。然而,对于单类别分类器,由于真实世界应用的动态性和正常类别的广泛范围,几乎仍然存在完全监督学习中出现的数据收集问题[4, 5]。在单类别分类器设置中,有可能将一个未见过的正常事件误分类为异常,因为其表示与从正常训练数据中学到的表示明显不同。
数据可用性问题导致一些研究人员定义了弱监督的视频异常检测(VAD),它不依赖于每帧的精细注释,而是使用视频级别的标签[11, 12]。具体而言,在完全监督的VAD中,每个单独的帧都有一个注释,指明它是正常的还是异常的。相反,在弱监督的VAD中,即使视频中只有一个帧是异常的,整个视频也被标记为异常;而当视频的所有帧都是正常的时候,整个视频则被标记为正常。尽管执行这样的标注似乎相对较便宜,但需要注意的是,在弱监督设置中,(a) 将视频标记为正常仍然需要检查整个帧(类似于完全监督设置),而且 (b) 这样的方法通常无法定位视频的异常部分,这可能在视频镜头很长时变得不切实际。
最近,Zaheer等人[13]定义了无监督的视频异常检测(VAD),它以未标记的视频作为输入,并学习为每一帧做出异常或正常的决策。与完全监督、弱监督和单类别方法相比,这种方式无疑更具挑战性,但它确实带来了不需要任何数据标注的优势。值得注意的是,无监督的视频异常检测[13]的定义与一类VAD有所区别,因为在一些研究中,后者被称为无监督[14, 15, 10, 16, 17, 18]。在一类VAD的情况下,训练数据分布仅表示正常性,这意味着仍然存在标注的概念。而无监督的视频异常检测[13]的实现对于训练数据的分布不做任何假设,从不使用标签进行模型训练,而是仅依赖于数据的时空特征。
在本研究中,我们通过利用信息丰富的未标记视频进行无监督的视频异常检测(VAD)。为此,我们仅依赖于扩散模型的重建能力[19](请参见图1以获取所提方法的描述)。这是第一次对扩散模型的有效性进行了在监控场景中进行VAD的调查。本研究的目的是进行一项探索性研究:
(a)了解扩散模型是否可以有效用于无监督的VAD
(b)发现扩散模型[19]在VAD方面的几个参数的行为。
在两个大规模数据集上进行的实验分析:UCF-Crime [2]和ShanghaiTech [3],表明所提方法始终优于VAD的最先进(SOTA)生成模型。此外,在某些情况下,所提方法能够超越更复杂的SOTA方法[13, 20]。我们的方法和SOTA [13]的代码可以在此处公开获取。
2. RELATEDWORK
异常检测是一个广泛研究的主题,涉及多个任务,如医学诊断、故障检测、动物行为理解和欺诈检测。感兴趣的读者可以参考最近的综述:[4]。以下是我们对监控场景中视频异常检测(VAD)的回顾。我们还介绍了扩散模型的定义和符号表示,并说明了我们在VAD中遵循的方法论。
在监控场景中的视频异常检测。通常,VAD被解决为一种离群检测任务(即一类分类器),其中模型是从正常的训练数据中学习的(需要数据注释),在测试期间,通过诸如基于距离的方法[21]、基于重建的方法[8]或基于概率的方法[22]等途径检测异常。由于在训练过程中排除了异常类别,这些方法可能导致无效的分类器。特别是当不能在训练中使用足够表示每个正常类别变体的数据时,这种情况可能会发生。另一种方法是使用未标记的训练数据,而不假设任何正常性[13],被称为(完全)无监督的VAD。与一类分类器不同,无监督的VAD不需要数据标注,并且可以通过在训练中不排除异常数据来潜在地具有很好的泛化性。Zaheer等人[13]提出了一种生成式协同学习方法,由生成器和鉴别器组成,二者共同进行训练,采用负学习范式。生成器是一个自动编码器,用负学习方法重建正常和异常的表示,同时利用负学习方法帮助鉴别器估计一个实例被判定为异常的概率,使用数据驱动的阈值。该方法[13]符合异常事件较正常事件更少且事件通常在时间上一致的观点。在本研究中,我们遵循[13]中的无监督VAD定义。与[13]不同的是,我们的方法仅依赖于一个生成架构,即基于扩散模型。在本研究中,我们首次调查了扩散模型在监控场景中用于VAD的有效性,通过报告个体参数如何影响模型性能,并将其与SOTA进行比较。
Diffusion Models.扩散模型(DMs)[23, 24]是一种生成模型,通过向训练样本添加噪声并学习逆转该过程的能力,获得生成各种样本的能力。这些模型在文本到图像合成[25]、语义编辑[26]和音频合成[27]等任务中取得了最先进的性能。它们还在用于具有判别性任务的表示学习,如目标检测[28]、图像分割[29]和疾病检测[30]。本研究是首次尝试将扩散模型应用于视频异常检测。
扩散模型(DMs)的数学表达式是对输入数据点
x
T
x_T
xT?采样自标准差为
σ
d
a
t
a
σ_{data}
σdata?的分布
p
d
a
t
a
(
x
)
p_{data}(x)
pdata?(x) 的过程,通过逐步添加标准差为 σ 的高斯噪声。对于
σ
?
σ
d
a
t
a
σ ? σ{data}
σ?σdata,受噪声影响的分布
p
(
x
,
σ
)
p(x, σ)
p(x,σ)变得各向同性,允许从分布中采样一个点
x
0
~
N
(
0
,
σ
m
a
x
I
)
x_0 ~ N(0, σ_{max}I)
x0?~N(0,σmax?I)。然后,逐渐将这一点通过噪声级别
σ
0
=
σ
m
a
x
>
σ
T
?
1
>
?
?
?
>
σ
1
>
σ
T
=
0
σ_0 = σ_{max} > σ_{T?1} > · · · > σ_1 > σ_T = 0
σ0?=σmax?>σT?1?>???>σ1?>σT?=0 逐渐去噪,生成新的样本,这些样本的分布符合数据集的分布。DMs使用去噪分数匹配(Denoising Score Matching)[31]进行训练,其中去噪器函数
D
θ
(
x
;
σ
)
D_θ(x; σ)
Dθ?(x;σ)最小化对于从
p
d
a
t
a
p_{data}
pdata? 中抽取的每个
σ
σ
σ的样本的期望
L
2
L2
L2去噪误差:
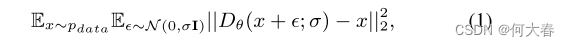
并且在相反过程中使用的评分函数变为:
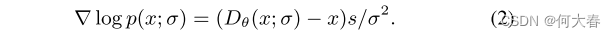
在本文中,我们采用了[19]的扩散模型,其细节将在下一节中描述。
3. METHOD
给定一个视频片段,我们首先从一个3D-CNN(F)中提取特征,在训练和测试阶段都使用这些特征。这些特征被提供给生成器,即扩散模型,以在不使用标签的情况下对其进行重构。我们遵循[19]中提出的扩散模型变体,并将其称为k-diffusion。它解开了先前扩散模型的设计选择,并提供了一个框架,其中每个组件都可以单独调整,如表1所示。

具体而言,Karras等人[19]提出了一个问题,即期望网络
D
θ
D_θ
Dθ?在高噪声环境中(即当
σ
t
σ_t
σt?很高时)能够表现良好。为了解决这个问题,k-diffusion提出了一个
σ
σ
σ相关的跳连接,允许网络基于噪声的大小执行
x
0
x_0
x0?或
?
?
? - 预测,或介于两者之间。因此,去噪网络
D
θ
D_θ
Dθ?的表达式如下:
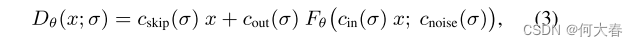
其中,
F
θ
F_θ
Fθ?成为需要训练的有效网络,
c
s
k
i
p
c_{skip}
cskip?调制了跳连接,
c
i
n
(
?
)
c_{in}(·)
cin?(?)和
c
o
u
t
(
?
)
c_{out}(·)
cout?(?)缩放输入和输出的大小,
c
n
o
i
s
e
(
?
)
c_{noise}(·)
cnoise?(?)缩放
σ
σ
σ以适应作为
F
θ
F_θ
Fθ?的输入。
在kdiffusion中,有几个超参数控制扩散过程,我们广泛探讨了训练噪声(按照参数 ( P m e a n , P s t d ) (P_{mean},P_{std}) (Pmean?,Pstd?)的对数正态分布分布)和采样噪声(具有 σ m i n σ_{min} σmin?和 σ m a x σ_{max} σmax?的边界值)的作用。这些分布是根据任务和数据集的不同而做的重要选择[32]。由于我们在前所未有的任务和新的数据集上使用扩散模型,我们不依赖于文献中的参数,而是在第4.2节中对噪声与任务性能之间的相关性进行了广泛研究。
扩散模型的逆过程不需要从方差为 σ m a x 2 σ^2_{max} σmax2? 的噪声开始,而可以从任意步骤$ t ∈ (0, T) $开始,其中 σ m a x 2 = σ 0 2 σ^2_{max} = σ^2_0 σmax2?=σ02?,如[26]所示。给定一个真实数据点 x x x,我们可以采样 x t ~ N ( x , σ t I ) x_t ~ N(x, σ_tI) xt?~N(x,σt?I),然后对 x T x_T xT? 应用逆过程。这允许保留原始数据点的一部分信息,即低频分量,并移除高频分量。我们利用这个特性通过添加高斯噪声来去除与视频片段中异常部分相关的分量。然后,我们使用均方误差(MSE)来衡量重构的好坏,这意味着高重构误差可能表明存在异常活动。对于这一过程的起始点 t 的选择是该方法的一个关键超参数,因为它控制了实现逼真性与忠实度之间的权衡,如[26]中所述。请参考第4.2节,进行了一项研究以了解该权衡对VAD的影响。
4. EXPERIMENTAL ANALYSIS AND RESULTS
作为评估指标,我们使用基于数据集测试视频的帧级注释计算的受试者工作特征(ROC)曲线下的面积(AUC),这与之前的研究一致。为了评估和比较所提方法的性能,我们在两个大规模的非受限数据集上进行实验:UCF-Crime [2] 和 ShanghaiTech [3]。UCF-Crime数据集[2]从各种不同视场的闭路电视摄像头中收集,总共包含128小时的视频,注释了13种不同的真实异常事件,如交通事故、偷窃和爆炸。我们使用数据集的标准训练(810个异常和800个正常视频,不使用标签)和测试(130个异常和150个正常视频)拆分,以与SOTA进行公平比较。ShanghaiTech数据集[3]是在13个不同的摄像机角度下捕获的,具有复杂的光照条件。我们使用包含63个异常和174个正常视频的训练拆分,以及包含44个异常和154个正常视频的测试拆分,这与SOTA一致。
我们使用3D-ResNext101和3D-ResNet18作为特征提取器F,因为它们在VAD中很受欢迎[4, 5, 13]。3D-ResNext101的维度为2048,而3D-ResNet18的维度为512。去噪网络D是一个具有编码器-解码器结构的MLP。编码器由大小为{1024,512,256}的3层组成,而解码器的结构为{256,512,1024}。模型的学习率调度器和EMA采用k-diffusion的默认值,初始学习率为 2 × 1 0 ? 4 2×10^-4 2×10?4,采用InverseLR调度;权重衰减设置为 1 × 1 0 ? 4 1×10^{-4} 1×10?4。特征提取的段大小设置为16个不重叠的帧,训练按照[13]进行,共进行50个epochs,批量大小为8192。时间步长 σ t σ_t σt?通过Fourier嵌入进行转换,并通过FiLM层[34]集成到网络中,分别位于网络的编码器和解码器部分。用于实现k-diffusion的超参数(例如, P m e a n P_{mean} Pmean?、P_{std}、 t t t)在第4.2节中给出。
4.1. Comparisons with State-Of-The-Art (SOTA)
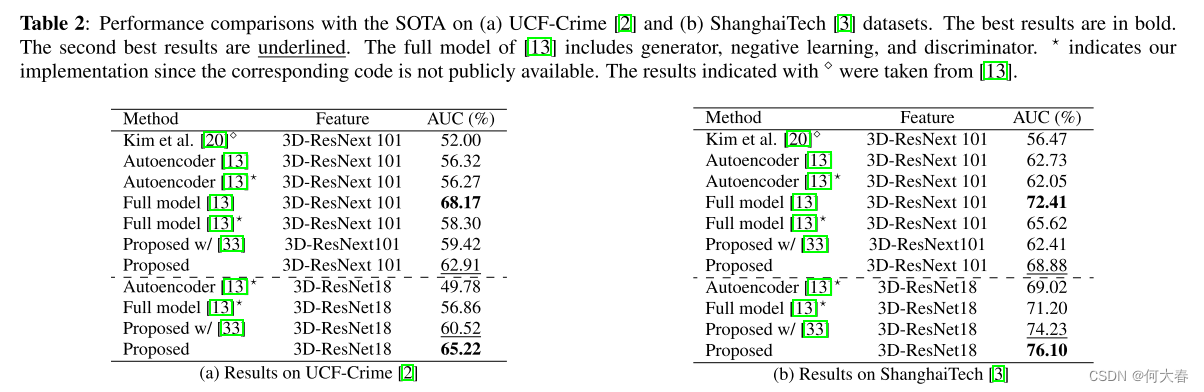
所提方法的性能与SOTA [20, 13]在表2中进行了比较。Kim等人[20]提出了一种一类VAD方法,然后在[13]中采用了这种方法来执行无监督的VAD。在我们的比较中,我们使用了[20]的无监督版本。所提方法在AUC上超过了[20]相当大的幅度:10.91-12.41%。与[13]的自动编码器进行的比较表明,作为生成模型,所提方法在VAD方面表现更好,AUC上的幅度为:6.15-14.44%。当使用从3D-ResNext101提取的特征时,[13]的完整模型获得了比所提方法更好的结果。这并不奇怪,因为[13]的完整模型比生成模型(即自动编码器或扩散模型)更复杂,因为它还包括鉴别器和负学习组件。重要的是,当3D-ResNet18作为骨干网络时,所提方法在AUC上超过了[13]的完整模型相当大的幅度:4.9-8.36%。这些结果证实了k-diffusion在执行VAD方面的显著有效性。
4.2. Diffusion Model Analysis
以下是k-diffusion模型不同超参数以及有关时间步嵌入的比较研究的效果。
噪声。在k-diffusion模型中,训练和采样噪声分布并不独立,我们计算了
(
P
m
e
a
n
,
P
s
t
d
)
(P_{mean}, P_{std})
(Pmean?,Pstd?)和
(
σ
m
i
n
,
σ
m
a
x
)
(σ_{min}, σ_{max})
(σmin?,σmax?)之间的关系,遵循以下公式:
σ
m
a
x
σ_{max}
σmax?,
σ
m
i
n
σ_{min}
σmin? =
e
P
m
e
a
n
±
5
P
s
t
d
e^{Pmean±5Pstd}
ePmean±5Pstd。这使我们能够将搜索限制在两个参数而不是四个参数上。我们还使用k-diffusion的默认参数提取了该公式:
P
m
e
a
n
=
?
1.2
P_{mean} = ?1.2
Pmean?=?1.2,
P
s
t
d
=
1.2
P_{std} = 1.2
Pstd?=1.2,
σ
m
i
n
=
0.02
σ_{min} = 0.02
σmin?=0.02和
σ
m
a
x
=
80
σ_{max} = 80
σmax?=80。当对ShanghaiTech数据集[3]使用3D-ResNet18且
L
t
h
L_{th}
Lth?的k取1时,相应的结果如图2所示。可以观察到,通常情况下,较小的
P
m
e
a
n
P_{mean}
Pmean?值导致更高的结果。这表明我们在一个行为良好的潜在空间中进行扩散,因此需要更小的噪声量才能达到各向同性高斯分布。

Starting point of the reverse process.类似于SDEdit [26]及其现实性与忠实度的权衡,我们探讨了不同起始点t对反向过程的影响。回想一下 σ t > σ t + 1 σ_t > σ_{t+1} σt?>σt+1?意味着 t t t接近零表示受噪声影响的 x t x_t xt?更接近各向同性高斯分布,而 t 接近 T 表示所使用的特征更接近原始数据分布。我们旨在找到最佳的 t 值,以便在保留关于视频片段结构的足够信息的同时破坏可能异常的信息。通过这种方式,可以获得更高的重构误差,从而决定关联的视频帧是否异常。当 L t h L_{th} Lth?的k为1时,相应的结果如图2所示。t = best表示在给定固定的 P m e a n P_{mean} Pmean?、 P s t d P_{std} Pstd?组合下,从t = 0到 t = 9获得的最佳结果。对于ShanghaiTech数据集,使用3DResNet18骨干网络,大多数时间起始点t = 4导致最佳性能。所有结果中,当t = 6时观察到最佳结果。对于所有其他数据集和骨干网络组合,最佳结果是在t = 9时获得的。总体而言,对于固定的 P m e a n P_{mean} Pmean?、 P s t d P_{std} Pstd?组合,增加 t 值会提高VAD结果。
Threshold
L
t
h
L_{th}
Lth?。给定异常阈值
L
t
h
L_{th}
Lth? =
μ
p
μ_p
μp? +
k
σ
p
k σ_p
kσp?,通过将其值设置为0.1、0.3、0.5、0.7和1,研究了k的影响。对于3D-ResNext101,无论是在ShanghaiTech还是在UCF Crime中,最佳结果对应于k=0.5。对于3D-ResNet18,ShanghaiTech和UCF Crime中的最佳得分分别对应于k=0.7和0.1。当所有其他超参数的值保持不变时,更改k的值会导致AUC的最高和最低性能之间的差异高达3%。
Timestep embeddings.如前所述,我们的方法包括通过Fourier嵌入变换时间步
σ
t
σ_t
σt?,并通过FiLM层[34]将其整合到网络中。我们还采用了[33]的实现,它将时间步嵌入与其正弦和余弦值连接在一起(在表2中标为Proposed w/ [33])。结果证实了相对于所有情况下都优于[33]的我们的提议表现更好,同时在使用3D-ResNet18特征时都超过了SOTA。
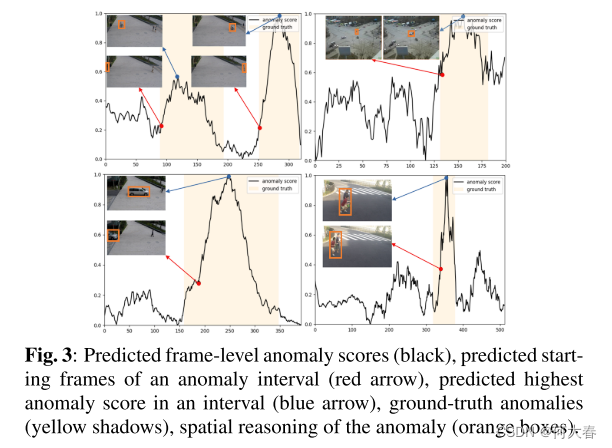
4.3. Qualitative Results
图3示出了由我们的方法产生的异常分数,例如视频剪辑。可以看出,与异常的类型无关,当地面实况异常开始时,异常分数立即增加,并且在地面实况异常结束后立即减少,这表明所提出的方法有利于VAD。
5. CONCLUSION
无监督视频异常检测(VAD)具有无需进行学习的数据注释的优势。这解决了正常和异常实例的异质性以及异常数据稀缺性带来的问题。本文是第一次尝试研究扩散模型在视频监控中进行VAD的能力,我们特别研究了将高重构误差作为异常指示的可能性。在流行的基准数据上进行的实验证明,与SOTA生成模型(无论使用的特征提取器是什么)相比,所提出的模型实现了更好的性能。我们的模型虽然仅依赖于时空数据的重构,在某些情况下却能够超越更复杂的方法,例如执行生成和判别网络的协作学习的方法。我们还提供了有关如何在VAD中使用扩散模型(特别是k-diffusion [19]的公式)的多个参数的指南。未来的工作包括研究我们的方法在跨数据集设置中的泛化能力。
阅读总结
无,只是翻译了一下
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Fragstats景观格局指数计算入门教程
- Webservice--HTTP,SOAP协议区别
- C++ 创建引用变量
- 【漏洞复现】Hikvision综合安防管理平台Fastjson命令执行漏洞
- 【算法】【哈希表,回溯,位运算】力扣2397. 被列覆盖的最多行数
- C# Wpf MVVM 框架下的线程并发与异步编程
- 【深度学习目标检测】十一、基于深度学习的电网绝缘子缺陷识别(python,目标检测,yolov8)
- 阿里云公有云平台
- 135 二叉树的最小深度
- [贪心算法] 国王游戏