论文阅读《Rethinking Efficient Lane Detection via Curve Modeling》
目录
3.3. End-to-end Fit of a B′ezier Curve
4.6. Limitations and Discussions
B. Specifications for Compared Methods
C. B′ezier Curve Implementation Details
D. IoU Loss for B′ezier Curves
E. GT and Prediction Matching Prior
Abstract
这篇论文提出了一种新颖的基于参数曲线的方法,用于在RGB图像中进行车道线检测。与通常需要启发式方法来解码预测或制定大量锚点的先进的基于分割和点检测的方法不同,基于曲线的方法可以自然地学习整体的车道表示。为了处理现有多项式曲线方法的优化困难,我们提出利用参数化的贝塞尔曲线,因为它易于计算、稳定,并且具有高自由度的变换。此外,我们提出了基于可变形卷积的特征翻转融合,以利用驾驶场景中车道的对称性质。所提出的方法在流行的LLAMAS基准测试中实现了新的最先进性能。在TuSimple和CULane数据集上,它也取得了良好的准确性,同时保持了低延迟(>150 FPS)和小模型大小(<10M)。我们的方法可以作为车道检测参数曲线建模的新基线,为自动驾驶感知提供新的参考。我们的模型代码以及PytorchAutoDrive: 一个用于自动驾驶感知的统一框架,可在https://github.com/voldemortX/pytorch-auto-drive找到。
1. Introduction
车道检测是自动驾驶系统中的一项基础任务,它支持车道保持、居中和变换等决策。先前的车道检测方法[2, 12]通常依赖于昂贵的传感器,如激光雷达(LIDAR)。随着深度学习技术的快速发展,许多研究[19, 21, 22, 33, 41]提出了从商用前置摄像头捕获的RGB图像中检测车道线的方法。
深度车道检测方法可以分为三类,即基于分割、基于点检测和基于曲线的方法(图1)。在这些方法中,基于分割和基于点检测的方法通常通过依赖经典分割[5]和目标检测[28]网络来实现最先进的车道检测性能。基于分割的方法[21,22,41]利用前景纹理线索对车道像素进行分割,并通过启发式方法将这些像素解码为线实例。基于点检测的方法[15,33,39]通常采用R-CNN框架[9,28],通过检测密集点系列(例如,垂直轴上的每10个像素一个点)来检测车道线。这两种方法都通过间接的代理(即分割图和点)表示车道线。为了处理对整体车道线的学习,在遮挡或恶劣的天气/光照条件下,它们不得不依赖于低效的设计,例如循环特征聚合(对于实时任务来说太重)[22,41],或者大量的启发式锚点(> 1000,可能偏向于数据集统计)[33]。
另一方面,目前只有少数几种方法[19, 32]被提出来将车道线建模为整体曲线(通常是多项式曲线,例如 x = ay3 + by2 + cy + d)。尽管我们期望整体曲线是一种简洁而优雅的方式来模拟车道线的几何属性,但抽象的多项式系数很难学习。先前的研究表明,这些方法的性能远远落后于设计良好的基于分割和基于点检测的方法(在CULane [22]数据集上与最先进的方法相比差距高达8%)。在本文中,我们旨在回答这样一个问题:是否有可能构建一个最先进的基于曲线的车道检测器。
我们观察到,经典的三次贝塞尔曲线在参数化驾驶场景中车道线的形变时具有足够的自由度,保持低计算复杂性和高稳定性。这启发我们提出通过贝塞尔曲线对车道线的细长几何形状进行建模。通过在图像上的贝塞尔控制点进行优化的便利性使得网络可以通过双向匹配损失 [38] 进行端到端的学习,使用来自简单的逐列池化(例如,在CULane数据集上使用50个提案)的稀疏车道提案集,无需任何后处理步骤,如非极大值抑制(NMS)或手工制作的启发式方法,例如锚点,因此实现了高速度和小模型尺寸。此外,我们观察到从前置摄像头(例如,车道之间或左右车道之间)观察到的车道线呈对称形状。为了建模驾驶场景的这种全局结构,我们进一步提出了特征翻转融合,通过聚合特征图及其水平翻转版本来加强这种共存。我们基于可变形卷积 [42] 的特征翻转融合设计,以对齐由旋转相机、变道、非配对线等引起的不完美对称性。我们进行了大量实验证明我们方法的性质,并展示在三个流行的基准数据集上,它相对于最先进的车道检测器表现良好。我们的主要贡献总结如下:
我们提出了一种新颖的基于Bézier曲线的深度车道检测器,能够有效地建模车道线的几何形状,并在恶劣驾驶条件下具有自然的鲁棒性。
我们提出了一种新颖的基于可变形卷积的特征翻转融合模块,以利用从前视摄像头观察到的车道的对称性质。
通过在三个流行的车道检测数据集上进行广泛的实验证明,我们的方法速度快、轻量级且准确。具体而言,我们的方法在LLAMAS基准[3]上,使用轻量级的ResNet-34骨干网,优于所有现有方法。
2. Related Work
Segmentation-based Lane Detection.??这些方法将车道检测表示为逐像素分割。SCNN [22] 将车道检测表述为多类别语义分割,是TuSimple挑战 [1] 中第一名解决方案的基础。其核心的空间卷积神经网络模块通过循环聚合空间信息以完成不连续的分割预测,然后需要启发式后处理来解码分割地图。因此,它具有较高的延迟,并且仅在由郑等人进行的优化之后才努力实现实时性 [41]。其他方法探索知识蒸馏 [13] 或生成建模 [8],但它们的性能仅略优于经典的SCNN。此外,这些方法通常假设存在一个固定数量(例如,4)的车道线。LaneNet [21] 利用实例分割流程来处理可变数量的车道线,但它需要在推理后进行聚类以生成车道线实例。一些方法采用了逐行分类 [26, 40],这是对逐像素分割的自定义下采样,因此它们仍然需要进行后处理。Qin等人 [26] 提出为了低延迟而牺牲性能,但是他们使用全连接层导致模型体积较大。
简而言之,基于分割的方法通常需要进行大量的后处理,这是因为表示的不对齐。它们还受到分割任务的局限性的影响,因此在遮挡或极端光照条件下往往表现较差。
Point Detection-based Lane Detection.??目标检测方法的成功驱使研究人员将车道检测任务转变为检测车道的一系列点(例如,在垂直轴上每10个像素)。Line-CNN [15] 将经典的Faster R-CNN [28] 调整为一阶段车道线检测器,但推理速度较慢(<30 FPS)。后来,LaneATT [33] 采用了更通用的一阶段检测方法,取得了更优越的性能。
然而,这些方法必须设计启发式车道锚点,这高度依赖于数据集统计,并需要进行非极大值抑制(NMS)作为后处理。相反,我们将车道线表示为具有完全端到端流程的曲线(无锚点,无NMS)。
Curve-based Lane Detection.??这项开创性的工作[37]提出了一个可微分的最小二乘拟合模块,用于将多项式曲线(例如,x = ay3 + by2 + cy + d)拟合到由深度神经网络预测的点上。PolyLaneNet[32]然后直接学习使用简单的全连接层来预测多项式系数。最近,LSTR[19]使用Transformer块以端到端的方式基于DETR[4]预测多项式。
曲线是对车道线的整体表示,自然地消除了遮挡,无需后处理,并且能够预测可变数量的车道线。然而,在大型和具有挑战性的数据集(例如 CULane [22] 和 LLAMAS [3])上,它们在性能上仍然落后于其他类别的方法。它们还面临收敛速度较慢的问题(例如,在 TuSimple 上需要超过 2000 个训练周期),以及高延迟的架构(例如,LSTR [19] 使用难以优化为低延迟的 transformer blocks)。我们将它们的失败归因于难以优化和抽象的多项式系数。我们提出使用参数化的贝塞尔曲线,该曲线由图像坐标系统上的实际控制点定义,以解决这些问题。
B′ezier curve in Deep Learning.??根据我们的了解,Bézier曲线在深度学习中的唯一已知成功应用是ABCNet [20],该网络在文本检测中使用了三次Bézier曲线。然而,他们的方法不能直接用于我们的任务。首先,该方法仍然使用非极大值抑制(NMS),因此无法实现端到端的训练。我们在我们的工作中表明,NMS是不必要的,因此我们的方法可以成为端到端的解决方案。其次,它直接在稀疏的Bézier控制点上计算L1损失,这导致了优化的困难。我们通过利用细粒度采样损失来解决这个问题。此外,我们提出了特别为车道检测任务设计的特征翻转融合模块。
3. B′ezierLaneNet
3.1. Overview
Preliminaries on B′ezier Curve.?Bézier曲线的表达式如下(Equation (1)),这是一条由 n + 1 个控制点定义的参数曲线:


![]()
我们使用经典的三次贝塞尔曲线(n = 3),经验上发现它足以用于建模车道线。与三阶多项式相比,它表现出更好的地面真实拟合能力(见表1),而三阶多项式是先前基于曲线的方法[19, 32]的基本函数。更高阶的曲线并未带来实质性的增益,而高自由度可能导致不稳定性。这里讨论的所有点的坐标都是相对于图像大小的(即主要在范围[0, 1]内)。?
The Proposed Architecture.?模型的总体架构如图2所示。具体而言,我们使用ResNets [11]的第三层特征作为骨干网络,采用RESA [41]的方法。但我们用两个具有膨胀率的膨胀块替换了骨干网络内部的膨胀。这对于我们的方法在速度和准确性之间取得更好的平衡,产生了一个下采样16倍的特征图,具有更大的感受野。然后,我们添加特征翻转融合模块(第3.2节)来聚合相对的车道特征。丰富的特征图(
)然后通过平均池化池化为(
),生成
个提案(对于CULane为50个)。我们使用两个
的1D卷积来转换池化特征,同时方便地对附近车道提案之间的相互作用进行建模,引导网络学习非极大值抑制(NMS)函数的替代方法。最后,最终预测由分类和回归分支获得(每个分支只有一个
的1D卷积)。输出为
,用于回归4个控制点,以及
,表示车道线对象的存在。
3.2. Feature Flip Fusion
通过将车道线建模为整体曲线,我们关注个体车道线的几何特性(例如,细长和连续)。现在,我们考虑来自车前摄像头视角的行驶场景中车道的全局结构。道路上的车道线等距分布,呈对称形态,这一性质值得建模。例如,左侧自车道线的存在很可能表明其右侧对应物的存在,即直观左车道的结构可能有助于描述直观右车道,等等。
为了利用这一特性,我们将特征图与其水平翻转版本融合在一起(图3)。具体来说,两个单独的卷积层和归一化层分别转换每个特征图,然后它们在通过 ReLU 激活之前相加在一起。通过这个模块,我们期望模型基于两个特征图进行预测。
为了考虑摄像机捕获图像的轻微不对齐(例如,旋转、转向、非配对),我们在学习偏移时对翻转的特征图应用可变形卷积[42],卷积核大小为3 × 3,同时根据原始特征图进行特征对齐。
我们在ResNet主干网络上添加了一个辅助的二进制分割分支,用于分割车道线和非车道线区域。在训练后,该分支将被移除。我们期望这个分支能够促使网络学习到更多的空间细节。有趣的是,我们发现只有在这个分支与特征融合一起工作时,性能才会提升。这是因为分割任务的局部化可能提供了更空间精确的特征图,从而支持在翻转特征之间进行准确的融合。
可视化结果如图4所示,从中我们可以看到翻转特征确实修正了汽车引入的不对称性导致的错误(图4(a))。
3.3. End-to-end Fit of a B′ezier Curve
Distances Between B′ezier Curves.?学习贝塞尔曲线的关键在于定义一个良好的距离度量,用于测量地面真实曲线与预测曲线之间的距离。一种直观的方法是直接计算曲线控制点之间的平均L1距离,就像ABCNet [20]中所做的那样。然而,如图5(a)所示,曲率控制点的较大L1误差可能表现为贝塞尔曲线之间非常小的视觉距离,特别是在小曲率或中等曲率的情况下(这在车道线的情况下经常发生)。由于贝塞尔曲线由参数t ∈ [0, 1]参数化,我们提出了更合理的贝塞尔曲线采样损失(图5(b)),通过在均匀间隔的一组t值(T)上对曲线进行采样,即相邻采样点之间的曲线长度相等。 t值可以通过重新参数化函数f(t)进一步转换。具体来说,给定贝塞尔曲线B(t)和预测曲线?B(t),采样损失Lreg定义如下:
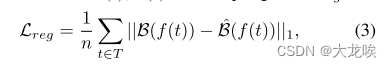
?其中n表示采样点的总数,设置为100。经验上发现f(t) = t效果良好。这种简单而有效的损失函数设置使得我们的模型更容易收敛,并且对于通常涉及到其他基于曲线或点检测方法的超参数,比如端点损失的权重[19]和线段长度损失[33](见图5(b,c)),我们的模型更不敏感。
B′ezier Ground Truth Generation.?现在我们介绍 Bézier 曲线地面实况的生成。由于车道数据集目前是通过在线关键点进行标注的,我们需要上述采样损失的 Bézier 控制点。给定车道线上的标注点 ,其中
表示第 i 个点的二维坐标。我们的目标是获得控制点
。与[20]类似,我们使用标准最小二乘拟合。
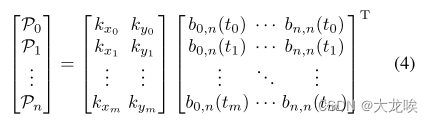
?其中,是从 0 到 1 均匀采样的。与文献 [20] 不同的是,我们不限制地面实况必须具有与原始注释相同的端点,从而得到更高质量的标签。
Label and Prediction Matching.??在训练中,获得了地面真实标签之后,我们通过使用最优二分图匹配来执行 G 个标签和 N 个预测之间的一对一关联(G < N),从而实现一个完全端到端的流程。遵循王等人 [38] 的方法,我们找到了 N 个预测的 G 个标签的最佳二分图匹配的 G 排列 ,具体构建如下:

?其中代表第 i 个标签与第 π(i) 个预测之间的匹配质量,基于曲线
之间的 L1 距离(采样损失)和类别得分
。默认情况下,
被设置为 0.8。以上方程可以通过著名的匈牙利算法有效地求解。
Wang等人[38]也使用了一种空间先验,将匹配的预测限制在标签的空间邻域内(物体中心距离,类似于FCOS中的中心性先验[35])。然而,由于许多车道是具有较大斜率的长线,这种中心性先验并不实用。更多关于匹配先验的研究请参见附录E。
Overall Loss.?除了 Bézier 曲线采样损失之外,还有用于车道对象分类(存在性)分支的分类损失 Lc。由于在车道检测中正负样本之间的不平衡程度没有目标检测那么严重,我们没有使用 Focal Loss [16],而是采用了简单的加权二元交叉熵损失:
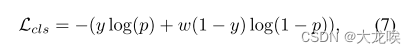
?其中 w 为负样本的权重,在所有的实验中被设定为 0.4。二进制分割分支(第 3.2 节)的损失 Lseg 采用相同的格式。
总损失是所有三种损失的加权和:

?其中,λ1、λ2、λ3分别被设置为1、0.1、0.75。
4. Experiments
4.1. Datasets
为评估我们提出的方法,我们在三个知名数据集上进行了实验:TuSimple [1]、CULane [22] 和 LLAMAS [3]。TuSimple 数据集是在高速公路上收集的,图像质量较高,天气条件良好。CULane 数据集包含更复杂的城市驾驶场景,包括阴影、极端光照和道路拥堵。LLAMAS 是一个新形成的大规模数据集,是唯一一个没有公开测试集标签的车道检测基准。这些数据集的详细信息可以在表2中找到。
4.2. Evalutaion Metics
对于 CULane 和 LLAMAS 数据集,官方评估指标是来自文献 [22] 的 F1 分数。
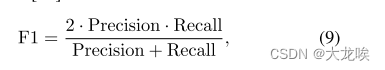
?其中精度?,召回率
。假设线为30像素宽,像素IoU超过0.5的预测和地面实况线被认为是匹配的。
对于TuSimple数据集,官方的评价指标包括准确率(Accuracy)、假正例率(False Positive Rate,FPR)和假负例率(False Negative Rate,FNR)。准确率的计算公式为,其中
是正确预测的在线点数,
是地面真实的在线点数。
4.3. Implementation Details
Fair Comparison.?为了公平地比较不同的最先进方法,我们在一个统一的PyTorch框架中重新实现了代表性的方法[19,22,41]。我们还提供了一个语义分割的基准线[5],最初在[22]中提出。我们所有的实现都没有在训练中使用验证集,并且只在验证集上调整超参数。一些具有可靠开源代码的方法是从它们自己的代码中报告的[26,32,33]。对于与平台相关的度量指标“每秒帧数”(FPS),我们在相同的RTX 2080 Ti平台上重新评估了所有报告的方法。有关实现和FPS测试的更多细节,请参见附录A到C。
Training.??我们在TuSimple、CULane 和 LLAMAS 数据集上分别进行了 400、36 和 20 个 epochs 的训练(在单个 RTX 2080 Ti GPU 上,我们的模型训练仅需 12 个 GPU 小时)。输入分辨率为 288×800 对于 CULane [22] 数据集,对于其他数据集为 360×640,符合通用实践。除此之外,所有超参数都是在 CULane [22] 的验证集上进行调优,并在所有数据集上保持一致。我们使用 Adam 优化器,学习率为,权重衰减为
,批量大小为 20,采用余弦退火学习率调度,与文献 [33] 中的方法相同。数据增强包括随机仿射变换、随机水平翻转和颜色抖动。
Testing.?曲线方法无需进行后处理。对于分割方法,我们会应用标准的高斯模糊和行选择后处理。LaneATT [33] 中使用了非极大值抑制(NMS),而我们在 CULane [22] 中去除了其后推断的 B-Spline 插值,以与我们的框架保持一致。
4.4. Comparisons
Overview.?实验结果显示在表3和表4中。TuSimple [1] 是一个小型数据集,具有清晰的天气、高速公路场景,并且具有相对较容易的评估指标,因此大多数方法在这个数据集上表现出色。因此,我们主要关注另外两个大型数据集 [3, 22],在这两个数据集中,各种方法之间仍然存在相当明显的差异。对于高性能方法(在CULane [22]上F1大于70%的方法),我们还在表5中展示了效率指标(FPS,参数数量)。
Comparison with Curve-based Methods.?正如表3和表4所示,在所有数据集中,BézierLaneNet在曲线识别方面表现优于先前的曲线方法[19, 32],并将基于曲线的方法的最新技术水平在CULane [22]上提高了6.85%,在LLAMAS [3]上提高了6.77%。由于我们采用了完全卷积和端到端的流水线,BézierLaneNet的运行速度比LSTR [19]快2倍。LSTR由于其Transformer架构存在速度瓶颈,1×和2×模型的帧率分别为98和97。虽然曲线学习具有一定难度,但我们的方法收敛速度比LSTR快4-5倍。首次,一种优雅的基于曲线的方法能够在这些数据集上挑战设计良好的分割方法或点检测方法,同时展现出良好的折衷,具有可接受的收敛时间。
Comparison with Segmentation-based Methods.?这些方法通常由于循环特征聚合[22, 41]和使用高分辨率特征图[5, 22, 41]而速度较慢。B′ezierLaneNet在速度和准确性方面均表现优异。即使与具有大型ResNet101骨干的RESA [41]和SCNN [22]相比,我们的小型模型在CULane [22]上也取得了明显的优势(1 ~ 2%)。在LLAMAS [3]上,数据集限制测试在4条中心线上,分割方法表现出色(表4)。尽管如此,我们的ResNet-34模型仍然在准确性上胜过SCNN 0.92%。
UFLD [26] 将分割问题重新制定为对降采样特征图的逐行分类,以实现更快的速度,但牺牲了准确性。与我们相比,在 CULane Normal 数据集上,UFLD(ResNet-34)准确性降低了0.9%,而在 Shadow、Crowd、Night 数据集上分别降低了7.4%,3.0%,3.2%。总体而言,我们的方法在相同的骨干网络下优于 UFLD 3% 到 5%,同时在 ResNet-34 上运行速度更快。此外,UFLD 使用大型全连接层以优化延迟,导致模型尺寸巨大(在表5中最大)。
所有分割方法的一个缺点是在极端的强光条件下,性能较差。基于像素的(或基于像素网格的,如UFLD [26])分割方法可能依赖于局部纹理的信息,而这些信息在强光照条件下会被破坏。而我们的方法预测车道线作为整体曲线,因此对局部纹理的变化具有鲁棒性。
Comparison with Point Detection-based Methods.??Xu等人[39]采用了一系列基于点检测的模型,利用神经架构搜索技术提出了CurveLanesNAS。尽管该方法采用了复杂的流程和广泛的架构搜索来在准确性和浮点运算操作(FLOPs)之间取得最佳平衡,但我们采用简单的ResNet-34骨干模型(29.9 GFLOPs)在CULane数据集上的性能仍然超过其大型模型(86.5 GFLOPs)0.8%。与分割方法在没有经过递归特征融合的情况下的类似缺点一样,CurveLanes-NAS在存在遮挡的情况下性能较差[5, 26]。如表3所示,与我们的ResNet-34模型相比,CurveLanes-NAS-M模型的模型容量相似(35.7 GFLOPs),在正常场景下性能差1.4%,但在阴影和拥挤场景中的差距分别为7.4%和2.7%。
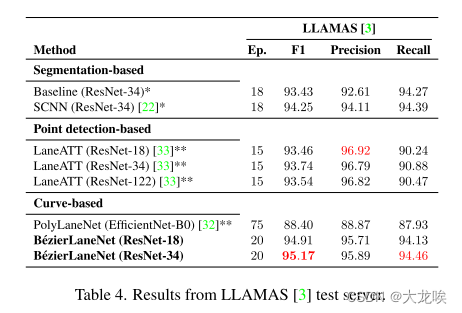
最近,LaneATT [33] 利用点检测网络实现了更高的性能。然而,他们的设计并非完全端到端(需要非极大值抑制(NMS)),基于启发式锚点(>1000),这些锚点直接从数据集的统计数据中计算而来,因此可能在泛化方面存在系统性的困难。尽管如此,在使用ResNet-34的情况下,我们的方法在LLAMAS [3]测试服务器上优于LaneATT(1.43%),并且具有显著更高的召回率(3.58%)。我们在仅使用TuSimple [1]训练集时达到了与LaneATT相当的性能,在CULane上仅差约1%。我们的方法在Dazzle Light方面表现显著更好(提高了3.3%),在Night方面相当(降低了0.4%)。甚至在交叉路口场景(Cross)上,尽管LaneATT表现出极低的假阳性特性(表4中的大Precision-Recall差距),我们的方法在假阳性率方面仍然更低。依赖启发式锚点[33]或启发式解码过程[22,26,39,41]的方法在这种场景中往往会有更多的错误预测。此外,NMS是一个顺序过程,在实际应用中可能具有不稳定的运行时。即使在实际输入上没有评估NMS,我们的模型在使用ResNet-18和ResNet-34骨干网络时分别比LaneATT快29%和28%,参数更少,分别为2.9×和2.3×。
总结一下,先前基于曲线的方法(例如 PolyLaneNet [32]、LSTR [19])在性能上明显较差。快速方法通常会在准确性(UFLD [26])或模型大小(UFLD [26]、LaneATT [33])方面进行权衡。准确的方法要么放弃端到端流水线(LaneATT [33]),要么无法满足实时要求(SCNN [22]、RESA [41])。而我们的 B′ezierLaneNet 则是完全端到端的,速度快(>150 FPS),轻量级(<10 million parameters),并在不同数据集上保持了一致的高准确性。
4.5. Analysis
虽然我们通过在验证集上调优了我们的方法,但我们重新运行了基于 ResNet-34 骨干网络的消融研究(包括我们的完整方法),并在 CULane 测试集上报告性能,以进行清晰的比较。
Importance of Parametric B′ezier Curve.?我们首先将 Bézier 曲线预测替换为三次多项式,并为起始点和终点添加辅助损失。如表6所示,尽管在我们的全卷积网络中进行了150个周期的训练(详见附录B.8),多项式在收敛方面表现得非常糟糕。然后,我们考虑修改 LSTR [19] 以预测立方 Bézier 曲线,但其性能与预测多项式相似。我们得出结论,学习多项式可能需要强大的 MLP [19, 32],而从位置感知 CNN 预测 Bézier 控制点是最好的选择。基于 transformer 的 LSTR 解码器破坏了精细的空间信息,抑制了曲线函数的进展。
Feature Flip Fusion Design.??如表7所示,特征翻转融合带来了4.07%的改善。我们还发现辅助分割损失可以进一步规范化并提高性能,提高了2.45%。值得注意的是,辅助损失只在特征融合的情况下起作用,当直接应用于基线时,可能导致退化结果(-3.07%)。标准的3×3卷积在添加辅助分割损失之前和之后均比可变形卷积差,分别下降了2.68%和1.44%。我们将这归因于特征对齐的影响。
B′ezier Curve Fitting Loss.?如表7所示,通过直接在控制点上使用损失替代采样损失导致性能下降(在基准设置中降低了5.15%)。受目标检测中IoU损失成功的启发,我们还为Bézier控制点的凸包实现了IoU损失(详细公式见附录D)。然而,接近直线车道的凸包太小,IoU损失在数值上不稳定,因此未能促进采样损失。
Importance of Strong Data Augmentation.?强大的数据增强通过一系列的仿射变换和颜色失真来定义,确切的策略可能会因不同的方法而略有不同。例如,我们使用随机仿射变换、随机水平翻转和颜色抖动。LSTR [19] 还使用了随机光照。默认的增强只包括一个小的旋转(3度)。正如表8所示,对于基于曲线的方法,强大的数据增强对于避免过拟合是至关重要的。
对于基于分割的方法[5, 22, 41],我们在较小的TuSimple[1]数据集上进行了快速的强增强验证。所有这些方法都显示了1 ~ 2%的性能下降。这表明它们可能由于逐像素预测和启发式后处理而具有一定的鲁棒性。但是,它们高度依赖于学习局部特征的分布,比如纹理,而这些特征在强增强的情况下可能变得混乱。
4.6. Limitations and Discussions
曲线确实是车道线的一种自然表示方法。然而,它们在建模方面的优雅性不可避免地带来了一个缺点。当数据分布高度偏斜时(在CULane中几乎所有车道线都是直线),曲率系数很难进行泛化。我们的贝塞尔曲线方法在一定程度上缓解了这个问题,并在CULane Curve中取得了可接受的性能(62.45)。在TuSimple和LLAMAS等数据集上,其中曲率分布相对公平,我们的方法取得了更好的性能。为了处理更广泛的情况,例如急转弯、阻塞和恶劣天气,像[30,34,39]这样的数据集可能会很有用。
特征翻转融合是专门为前置摄像头设计的,这是深度车道检测器的典型用例。然而,仍然存在一个强烈的归纳偏见,即假设场景对称。在未来的工作中,寻找替代这一模块的方法将会很有趣,以实现更好的泛化,并去除可变形卷积操作,这对于有效集成到Jetson等边缘设备中提出了挑战。
更多讨论见附录G。
5. Conclusions
在这篇论文中,我们提出了 BézierLaneNet:一种基于参数化 Bézier 曲线的全新端到端车道检测器。基于图像的 Bézier 曲线易于优化,并且自然地模拟了车道线的连续性,无需使用复杂的设计,如循环特征聚合或启发式锚点。此外,我们提出了一个特征翻转融合模块。它有效地模拟了驾驶场景的对称性,并通过使用可变卷积对轻微不对称性具有鲁棒性。所提出的模型在三个数据集上取得了良好的性能,在流行的 LLAMAS 基准测试中击败了所有现有方法。它还具有较快的推理速度(>150 FPS)和轻量级的特点(<10百万参数)。
Acknowledgements.?这项工作得到了中国国家重点研发计划(2019YFC1521104)、中国国家自然科学基金(61972157、72192821)、上海市科技重大项目(2021SHZDZX0102)、上海市科技委员会(21511101200)、国家社科基金艺术专项项目(I8ZD22)以及商汤公司合作研究资助。我们感谢秦佳平对道路设计和几何的指导,感谢龚雨辰和陈攀在类激活映射可视化方面的帮助,感谢龚志军、徐佳辰和龚靖宇对数学问题的深入讨论,感谢刘凤奇提供GPU支持,感谢Lucas Tabelini在评估[32, 33]方面的合作,以及感谢CVPR审稿人提供的建设性意见。
图和表
图
图1. 车道检测策略。基于分割和基于点检测的表示方法是局部且间接的。多项式曲线中使用的抽象系数(a、b、c、d)很难优化。三次贝塞尔曲线由4个实际存在的控制点定义,它大致拟合出线形状并包围车道线在其凸包内(虚线红线)。最好以彩色查看。
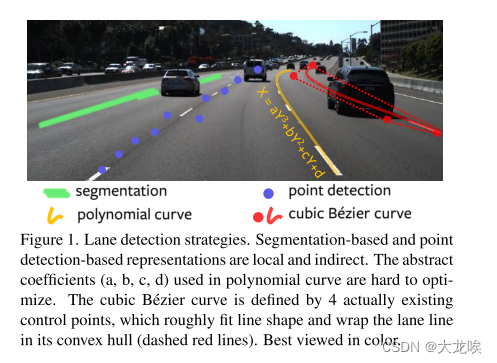
图2. 流程图。 通过典型编码器(例如ResNet)提取的特征通过特征翻转融合进行增强,然后被汇聚为1D,并应用两个1D卷积层。最后,网络通过一个分类分支和一个回归分支预测B′ezier曲线。
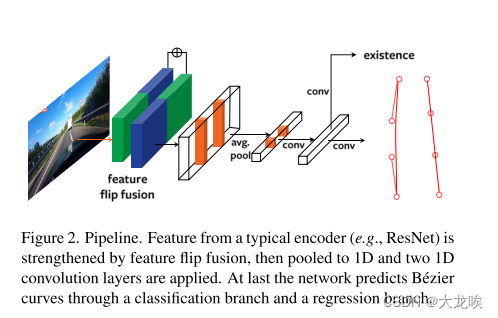
图3. 特征翻转融合。通过计算可变形卷积偏移,对翻转和原始特征图进行对齐。最佳查看颜色。
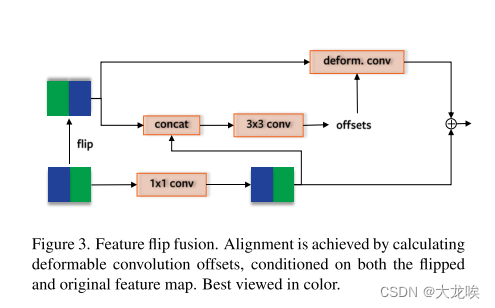
图4. 基于ResNet骨干网络最后一层的Grad-CAM [31] 可视化结果。 (a) 我们的模型能够从清晰的标线和对面道路上的车辆推断出一条模糊标线的存在。请注意,汽车偏向左侧,这个场景并没有完美对称地捕捉到。 (b) 当整个道路缺乏清晰标线时,我们利用两侧信息进行更好的预测。最好在彩色环境中查看。

?图5. 车道线损失函数。 (a) 控制点的L1距离与曲线之间的实际距离不高度相关。 (b) 提出的采样损失是一种通过t-采样的统一距离度量。 (c) 多项式回归的典型损失[19],至少需要3个独立的损失:y-采样损失,y起始点损失,y结束点损失。
?表
表1. 在TuSimple [1] 测试集上对n阶Bézier曲线和多项式的比较(数值越小越好)。由于官方度量过于宽松,难以显示出有意义的差异,因此我们使用了细粒度的LPD指标,遵循[32]的定义。

表2. 数据集详细信息。*LLAMAS数据集的行数超过4行,但官方指标只评估4行。

表3. 在CULane [22] 和 TuSimple [1] 测试集上的结果。*在我们的代码框架中再现的结果,最佳性能来自三次随机运行中的最好结果。**从作者的可靠开源代码中报告的结果。

?表4.来自LLAMAS [3]测试服务器的结果。
?表格 5. FPS(图像/秒)和模型大小。所有FPS结果均在相同平台上使用 360 × 640 随机输入进行测试。此处仅显示CULane [22] F1得分超过70%的模型。

?表6.曲线表示。基线直接预测曲线系数,无需特征翻转融合。

表7. 消融实验。CP: 控制点损失 [20]。SP: 提出的采样损失。Flip: 特征翻转融合模块。Deform: 在特征翻转融合中使用可变形卷积。Seg: 辅助分割损失。

?表8. 数据增强消融实验。增强:强化数据增强。

附录
Appendix Overview.?附录的组织结构如下:附录A描述了FPS测试协议和环境;附录B介绍了每种比较方法的实现细节(包括我们的在附录B.8中的细节);附录C提供了Bézier曲线的实现细节,包括采样、地面真值生成和变换;附录D为Bézier曲线制定了IoU损失并讨论了为何失败的原因;附录E探讨了除了中心性先验之外的匹配先验;附录F展示了关于CULane [22]之外的数据集的额外消融研究,以验证特征翻转融合的泛化性;附录G讨论了局限性并认识到该领域的新进展;附录H呈现了我们的方法在三个数据集上可视化的定性结果。
A. FPS Test Protocol
让一次每秒帧数(FPS)测试试验的平均运行时间为对具有其PyTorch[24]实现的模型进行100次连续推理,而不计算梯度。输入是一个3x360x640的随机张量(有些使用全1 [33],对速度没有影响)。请注意,所有方法都不使用像TensorRT这样的优化包。我们在计算整个运行时之前等待所有CUDA核心完成。我们使用Python的time.perf_counter(),因为它比time.time()更精确。对于所有方法,FPS报告为3次试验中的最佳结果。
在每次测试试验之前,我们进行至少10次前向传播作为设备的预热。对于每种新的测试方法,我们持续运行预热试验,直到达到与之前记录的帧每秒(FPS)相似的水平,以确保再次达到类似的峰值机器状态。
Evaluation Environment.?评估平台采用了一台装备有标准频率的2080 Ti GPU、搭载Intel Xeon-E3 CPU的服务器。该平台使用了CUDA 10.2、CuDNN 7.6.5以及PyTorch 1.6.0。FPS是一个受平台影响的度量标准,取决于GPU频率、环境条件、总线带宽、软件版本等因素。在使用2080 Ti的情况下,Tabelini等人在所有方法中都能够实现更好的峰值性能。因此,我们在所有FPS测试中都使用相同的平台,以提供公平的比较。
Remark.?请注意,FPS(每秒处理图像数)与吞吐量(每秒处理的图像数量)是不同的概念。由于FPS将批处理大小限制为1,因此更好地模拟了实时应用场景。而吞吐量考虑了批处理大小大于1的情况。LSTR [19] 报告了其最快模型的吞吐量为420 FPS,实际上是使用批处理大小为16的情况。我们重新测试的FPS为98。
B. Specifications for Compared Methods
B.1. Segmentation Baseline
这个分割基线是基于DeeplabV1 [5] 的,最初是在SCNN [22] 中提出的。实质上,它是没有使用条件随机场(CRF)的原始DeeplabV1,车道被视为不同的类别,并且使用一个独立的车道存在分支(一系列卷积、池化和多层感知机)来便于车道的后处理。我们基于最新的进展 [41] 对其进行了训练和测试方案的优化。在我们的代码库中重新实现后,它达到了比最近的论文通常报告的性能更高的水平。
Post-processing.?首先,通过车道存在分支确定是否存在车道。然后,将预测的每像素概率图插值到输入图像的大小。接下来,对预测进行9×9的高斯模糊,以平滑概率图。最后,对于每个存在的车道类别,通过预定义的Y坐标(量化),遍历平滑的概率图,并记录通过固定阈值的条件下,在行上概率最大位置的对应X坐标。具有少于两个合格点的车道将被简单地丢弃。
Data Augmentation.?我们使用了一种简单的随机旋转方法,旋转角度很小(3度),然后将图像调整为输入分辨率。
B.2. SCNN
我们的SCNN[22]是基于Torch7官方代码重新实现的。在作者的建议下,我们为空间CNN层添加了一种初始化技巧,并引入了学习率预热,以防止由于循环特征聚合导致的梯度爆炸。因此,我们可以安全地调整学习率。我们改进后的SCNN在性能上明显优于原始版本。
一些人可能会提到 SCNN 在 TuSimple 数据集上达到了 96.53% 的准确度,但需要注意这是通过使用外部数据进行训练的竞赛结果。我们在我们的代码库中报告的 SCNN 是使用相同的数据集(与其他重新实现的方法相同)并采用 ResNet 骨干网络进行训练的。
Post-processing.?同附录B.1。
Data Augmentation.?同附录B.1。
B.3. RESA
我们的 RESA 模型在实现上与其官方发布的代码有一些不同,主要的区别之一是我们没有在非车道区域进行切割(在每个数据集中,车道注释有一个特定的高度范围)。因为这个技巧是特定于数据集的,并且不具有普适性,我们没有在所有比较的方法中使用它。其他的差异都经过验证,至少在 CULane 验证集上表现更好,这些改进都在官方代码的基础上进行。
Post-processing.?同附录B.1。
Data Augmentation.?同附录B.1。原始 RESA 论文 [41] 中同样使用了随机水平翻转,但在我们的重新实现中发现这种方法并不有效。
B.4. UFLD
Ultra Fast Lane Detection (UFLD) [26] 是从他们的论文和开源代码中得到的。由于 TuSimple 数据集中的假正例(FP)和假负例(FN)的信息没有在论文中提供,而且使用源代码进行训练导致非常高的假正例率(接近20%),因此我们没有报告其在该数据集上的性能。我们调整了其性能分析脚本,以在我们的标准下计算参数数量和每秒帧数(FPS)。
Post-processing.?由于这种方法使用网格单元(每个单元等同于分割概率图中的若干像素),每个点的X坐标是通过位置(同一行的单元)的期望值计算的,即通过概率的加权平均。与分割后处理不同,这种方法可以被高效地实现。
Data Augmentation.?增强包括随机旋转和某种形式的随机平移。
B.5. PolyLaneNet
PolyLaneNet [32] 是从他们的论文和开源代码中报告的。我们在我们的标准中添加了一个性能分析脚本,用于计算参数数量和每秒帧数(FPS)。
Post-processing.?这种方法不需要后期处理。
Data Augmentation.?数据增强操作包括大范围的随机旋转(10度)、随机水平翻转和随机裁剪。它们以的概率应用。
B.6. LaneATT
LaneATT [33] 的参数和FPS的计算是根据他们的论文和开源代码进行的。我们调整了其性能分析脚本,以符合我们的标准。
Post-processing.?非极大值抑制(NMS)由一个自定义的CUDA核心实现。在测试和性能分析中,通过B样条对车道进行额外的插值被移除,因为它在CPU上执行速度较慢,而且提供的改善很小(约0.2%在CULane上)。
Data Augmentation.?LaneATT 使用随机的仿射变换,包括缩放、平移和旋转。同时,它还使用了随机的水平翻转。
Followup.?由于我们在提交截止日期前没有时间验证在我们的代码库中重新实现的 LaneATT 模型,因此 LaneATT 的性能仍然是从官方代码中报告的。我们的重新实现表明,除了在 CULane 上使用 ResNet-34 骨干网络的结果略微超出标准偏差范围之外,所有 LaneATT 的结果都是可复现的,但仍然在合理范围内。
B.7. LSTR
LSTR [19] 在我们的代码库中进行了重新实现。所有的 ResNet 骨干网络都是从 ImageNet [14] 预训练开始的。然而,LSTR [19] 使用了在 CULane(2×)中为 256 通道的 ResNet-18,而在其他数据集(1×)中为 128 通道,这使得无法直接使用现成的预训练 ResNets。尽管 ImageNet 预训练是否有助于车道检测仍然是一个未解之谜。我们在 CULane 上报告的 LSTR 性能是该数据集上的首次记录。通过调整超参数(学习率、迭代次数、预测阈值)、修复错误(原始分类分支具有 3 个输出通道,而应该是 2 个),我们在 CULane 上的性能比作者的试验提高了 4%。具体而言,我们使用学习率为 2.5 × 10^(-4),批量大小为 20,分别进行了 150 和 2000 个 epochs,在 CULane 和 TuSimple 上使用了 0.95 和 0.5 的预测阈值。在 TuSimple 中使用较低的阈值是因为官方测试指标更倾向于高召回率,然而,对于实际应用来说,高召回率会导致高假阳性率,这是不希望看到的。
我们在进行 LSTR-Bezier 实验时,通过将曲线损失的权重除以 10,这是因为我们在该实验中使用了 100 个采样点,这些点具有 X 和 Y 坐标,需要进行拟合。因此,该损失的规模大约是原始损失的 10 倍(LSTR 损失采用点 L1 距离的求和而不是平均值)。通过这种调整,我们实现了与原始 LSTR 相似的损失景观。
Post-processing.?这种方法不需要后期处理。
Data Augmentation.数据增强包括PolyLaneNet的(附录B.5),然后添加了随机颜色失真(亮度、对比度、饱和度、色调)以及从COCO数据集[17]计算得出的光源进行的随机照明。这是迄今为止在这一研究领域中最复杂的数据增强流程,我们已验证该流程的所有组件都有助于LSTR的训练。
Remark.?LSTR的多项式系数无界,导致数值不稳定(而二分图匹配需要精度),以及训练的高失败率。在CULane上,fp32训练的失败率约为30%。在BezierLaneNet中,这个问题得以解决,因为我们的L1损失可以被限制在[0, 1]范围内,而不影响学习(控制点可以轻松收敛到图像上)。
B.8. B′ezierLaneNet
BézierLaneNet是在相同的代码框架中实现的,我们在这个框架中重新实现了其他方法。与LSTR一样,默认的预测阈值被设置为0.95,而在TuSimple中使用的是0.5 [1]。
Post-processing.?这种方法不需要后期处理。
Data Augmentation.我们使用的数据增强方法类似于LSTR(附录B.7)。具体而言,我们移除了LSTR中的随机光照(为了严格避免使用外部数据的知识),并将PolyLaneNet中的几率增强替换为随机仿射变换和随机水平翻转,就像LaneATT一样(附录B.6)。随机仿射变换的参数包括:旋转(最多10度)、平移(X轴最多50像素,Y轴最多20像素)、缩放(最多20%)。
Polynomial Ablations.?在多项式消融实验(表7)中,我们修改了网络以预测第三阶多项式的6个系数(4个曲线系数和起始/结束的Y坐标)。类似于LSTR [19],我们为起始/结束的Y坐标添加了额外的L1损失。通过大量的尝试(调整学习率、损失权重、训练轮数),即使在完整的BezierLaneNet设置下,在CULane数据集上进行了150轮训练,模型仍然无法收敛到足够好的解决方案。换句话说,无法达到足够精确以通过CULane度量标准。在多项式曲线上的采样损失只能达到0.02,这意味着在训练集上的平均X坐标误差为0.02 × 1640像素 = 32.8像素。CULane要求曲线之间的IoU为0.5,这些曲线被扩展到30像素宽,因此至少需要大约10像素的平均误差才能获得有意义的结果。通过将IoU要求放宽到0.3,我们可以获得“BezierLaneNet的第三多项式”F1分数为15.82。尽管审查委员会建议对这个消融实验添加简单的正则化以促使收敛,可惜我们未能做到这一点。
C. B′ezier Curve Implementation Details
Fast Sampling.?贝塞尔曲线的采样可能因为复杂的伯恩斯坦基多项式而显得繁琐。为了通过一系列固定的 t 值快速采样贝塞尔曲线,可以事先计算伯恩斯坦基多项式的结果,从而只需进行一次简单的矩阵乘法。
Remarks on GT Generation.?Bézier曲线的地面实况是通过最小二乘拟合生成的,这是一种多项式拟合的常见技术。我们选择这种方法是因为它简单易懂,并且事实上已经表现出接近完美的车道线拟合能力(在CULane测试和LLAMAS验证集上分别达到99.996和99.72的F1分数)。然而,对于参数曲线来说,这并不是一种理想的算法。有一个专门的研究领域,致力于找到比最小二乘法更好的Bézier曲线拟合算法[23]。
B′ezier Curve Transform.?在贝塞尔曲线上应用仿射变换时遇到的一个实现困难是如何处理仿射变换对于控制点的影响(用于在数据增强中转换地面实况曲线)。从数学上讲,在控制点上的仿射变换等效于对整个曲线进行仿射变换。然而,平移或旋转可能会将控制点移出图像。在这种情况下,需要对贝塞尔曲线进行切割。经典的 De Casteljau 算法用于切割图像上的贝塞尔曲线段。假设一个连续的图像上段,有效的采样点范围为 t = t0 到 t = t1。将一个由控制点 P0、P1、P2、P3 定义的三次贝塞尔曲线切割为其图像上的段 P'0、P'1、P'2、P'3 的公式为:

其中。这个公式可以通过矩阵乘法高效实现。在车道检测数据集上,非连续的三次贝塞尔曲线的可能性非常低,因此为简化起见被忽略。即使发生这种情况,方程(10)也不会改变曲线,而我们的网络仍然可以预测图像之外的控制点,这些控制点仍然适用于图像上的车道线段。
D. IoU Loss for B′ezier Curves
在这里,我们简要介绍了如何构建 Bézier 曲线之间的 IoU 损失。在深入算法之前,有两个前提条件:
极坐标排序(Polar sort):通过在N边形内的任意点作为锚点,该N边形的顶点为
(通常为顶点坐标的均值,即
),通过其atan2角度对顶点进行排序。这将返回一个按顺时针或逆时针排列的多边形。
凸多边形面积:一个有序的凸多边形可以通过简单的索引操作高效地分割成相邻的三角形。凸多边形的面积是这些三角形的和。三角形((x1, y1), (x2, y2), (x3, y3))的面积S计算公式如下:
假设我们有两个由贝塞尔曲线生成的凸多边形(有许多凸包算法可用)。现在,将贝塞尔曲线之间的IoU(交并比)转化为凸多边形之间的IoU。基于一个简单的事实,即凸多边形的交集仍然是一个凸多边形,经过对所有凸包进行极坐标排序并确定相交的多边形后,我们可以将IoU计算轻松表示为一系列凸多边形面积计算。难点在于如何高效地确定凸多边形对之间的交集。
考虑两个相交的凸多边形,它们的交集包括两种类型的顶点:
-
交点(Intersections): 边之间的交点,即两个多边形的边相交的点。
-
内部点(Insiders): 存在于两个多边形内部或边界上的顶点。
在处理交叉点时,我们首先将每个多边形的边表示为通用的直线方程:ax + by = c。然后,对于直线和直线
,交点
的计算公式如下:

?其中 。在各自的线段上的所有
都是交点。
对于Insiders,定义如下:
定义1:对于一个凸多边形,位于每条边同一侧的点 P(x, y) 被视为在多边形内部。
一个排序的凸多边形是由一系列边组成的(由 P0(x0, y0) 和 P1(x1, y1) 定义的线段),判断一个点在线段的哪一侧的方程如下:
![]()
sign > 0 意味着点 P 在直线的右侧,sign < 0 表示点 P 在直线的左侧,而 sign = 0 表示点 P 在直线段上。需要注意的是,对于浮点数计算,等式 sign = 0 不是稳定的操作。但在编码中有简单的方法来解决这个问题,这里我们不详细展开。
上述公式可以通过矩阵操作和索引实现,以有效地确定交叉点和内部点。这种方法使得可以迅速地对批量输入进行训练。
终,在能够计算凸多边形的交集和面积之后,广义IoU损失(GIoU)就可以简单地表示为(如文献[29]中所述):

并集(Union)的计算可以表示为 A ∪ B = A + B ? A ∩ B。包围凸对象 C 可以通过两个凸多边形的凸包计算得出,或者通过包围矩形进行上界限制。我们在 PyTorch 中纯粹实现了 IoU(交并比)计算[24],我们的实现运行时仅比矩形 IoU 损失计算的运行时多约 5 倍。
然而,根据道路设计规定 [7, 36],车道线大多是直线。这导致 B′ezier 曲线的凸包区域非常小,因此在优化过程中引入了数值不稳定性。尽管在一个玩具多边形拟合实验中取得了成功,但我们目前未能观察到损失的收敛,以促进在车道数据集上的学习。
E. GT and Prediction Matching Prior
我们不采用中心度先验,而是尝试使用局部最大先验,即限制匹配预测具有局部最大分类Logit。这种先验可以帮助模型理解车道线的空间稀疏结构。如图6所示,用于分类Logit的学习特征激活呈现出与实际驾驶场景相似的结构。

F. Extra Results
表 9. 在TuSimple测试集(准确率)和LLAMAS验证集(F1分数)上的消融研究,包括添加特征翻转融合模块之前和之后的结果。使用ResNet-34作为骨干网络,由于在这些数据集上进行的消融研究通常不够稳定,难以显示方法之间的明显差异,因此报告3次平均值。

G. Discussions
存在一种基于侧视图的车道检测器的原始应用,用于估算到可驶动区域边界的距离[10],这与特征翻转融合的使用相矛盾。在这种情况下,可能一个较低阶的Bézier曲线基准线(使用行向而不是列向池化)就足够了。这超出了本文的关注范围。
Recent Progress.??最近,一些研究者尝试了不完全符合传统三类(分割、点检测、曲线)的车道表示或形式化方法。与流行的自顶向下方法不同,[27] 提出了一种自底向上的方法,重点关注局部细节。[18] 实现了最先进的性能,但是由于车道线的复杂条件解码,导致运行时不稳定,这对于实时系统并不理想。
H. Qualitative Results
定性结果如图7所示,使用我们的ResNet-34骨干模型。对于每个数据集,以两行的形式展示了4个结果:第一行展示了定性成功的预测;第二行展示了典型的失败案例。
TuSimple.?正如图7(a)所示,我们的模型很好地适应了高速公路曲线,仅在图像的远侧出现了轻微的误差,这里的图像细节被投影破坏。我们的典型失败案例是高FP率,主要归因于使用了较低的阈值(附录B.8)。然而,在右下方的宽道场景中,我们的FP预测实际上是一条有意义的车道线,但在中心线注释中被忽略。
CULane.?正如图7(b)所示,该数据集中的大多数车道都是直的。我们的模型能够在拥堵情况(左上)和阴影(右上,由树木投下的阴影)下进行准确的预测。典型的失败案例是在遮挡下的预测不准确的情况(第二行),在这些情况下,人们通常无法从视觉上判断哪个更好(地面真实情况还是我们的FP预测)。
LLAMAS.?如图7(c)所示,我们的方法在清晰的直线(左上方)上表现出色,对于一个充满阴影的具有较大曲率的复杂场景也具有良好的性能。在左下方的图像中,我们的模型在光照较低、路面有瑕疵的情况下表现不佳。而在另一低照明场景(右下方),来自激光雷达和高清地图的无监督标注被白色箭头误导(请注意右侧蓝线的锯齿状形状)。
图7. B′ezierLaneNet(ResNet-34)在验证集上的定性结果。红色标记的是误检(False Positives,FP),绿色标记的是正确检测(True Positives,TP),蓝色绘制的是真实标注。几乎看不见的蓝线正好被绿线精确覆盖。B′ezier曲线的控制点用实心圆标记。为了对齐,图像略微调整大小。最佳观看方式为彩色图,2×放大。

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Open3D 读写并显示PCD文件 (1)
- 二叉树..
- grep输出匹配行及之后几行用 -A 数值
- 前后对比效果展示的视频怎么制作?左右对比PR模板 Before and After v.2
- vue.config.js中打包相关配置
- 使用 Jamf Pro 和 Okta 工作流程实现自动化苹果设备管理
- 锐捷配置路由重发布中的度量修改
- CSS学习之-06
- leaflet 使用antpath加载河流流动效果
- 医院患者满意度调查问卷示例