【算法练习Day50】下一个更大元素II&&接雨水

?📝个人主页：@Sherry的成长之路
🏠学习社区：Sherry的成长之路（个人社区）
📖专栏链接：练题
🎯长路漫漫浩浩，万事皆有期待

下一个更大元素II

503. 下一个更大元素 II - 力扣（LeetCode）

给定一个循环数组 nums （ nums[nums.length - 1] 的下一个元素是 nums[0] ），返回 nums 中每个元素的 下一个更大元素 。

数字 x 的 下一个更大的元素 是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1 。

在遍历的过程中模拟走了两边nums。

class Solution {
    public int[] nextGreaterElements(int[] nums) {
        Stack<Integer> st = new Stack<>();
        int[] result = new int[nums.length];
        Arrays.fill(result, -1);

        st.push(0);
        for (int i = 1; i < 2 * nums.length; i++) {
            while (!st.isEmpty() && nums[i%nums.length] > nums[st.peek()]) {
                result[st.pop()] = nums[i % nums.length];
            }
            st.push(i % nums.length);
        }
        return result;
    }
}

接雨水

42. 接雨水 - 力扣（LeetCode）

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

单调栈思路

1.首先单调栈是按照行方向来计算雨水，如图：

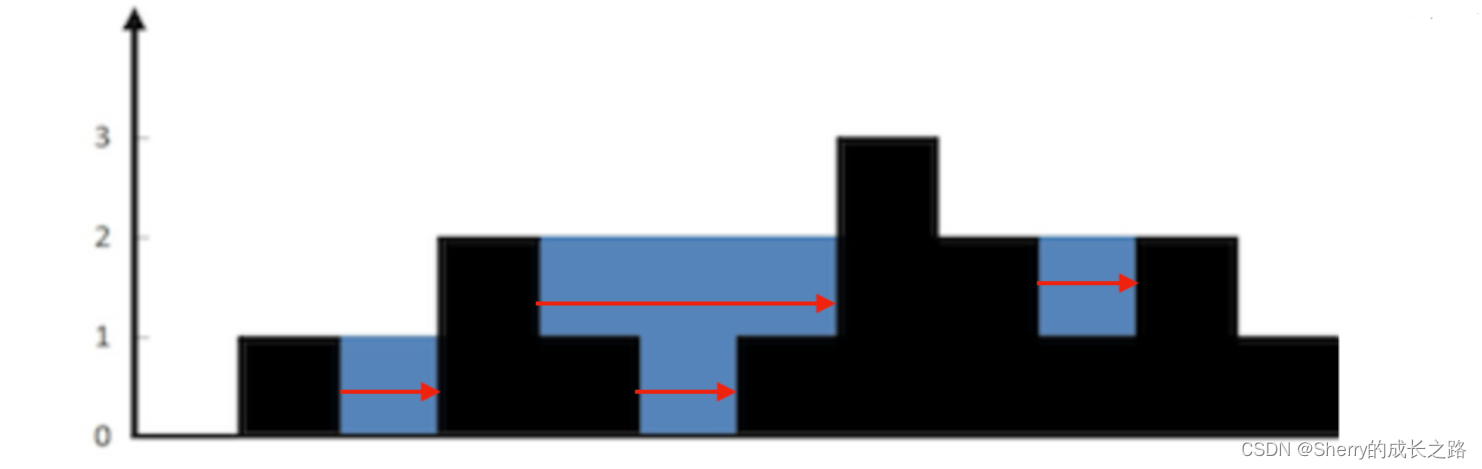
在这种情况下，可以接6个单位的雨水

2.使用单调栈内元素的顺序

从大到小还是从小到大呢？

从栈头（元素从栈头弹出）到栈底的顺序应该是从小到大的顺序。

因为一旦发现添加的柱子高度大于栈头元素了，此时就出现凹槽了，栈头元素就是凹槽底部的柱子，栈头第二个元素就是凹槽左边的柱子，而添加的元素就是凹槽右边的柱子。

如图：

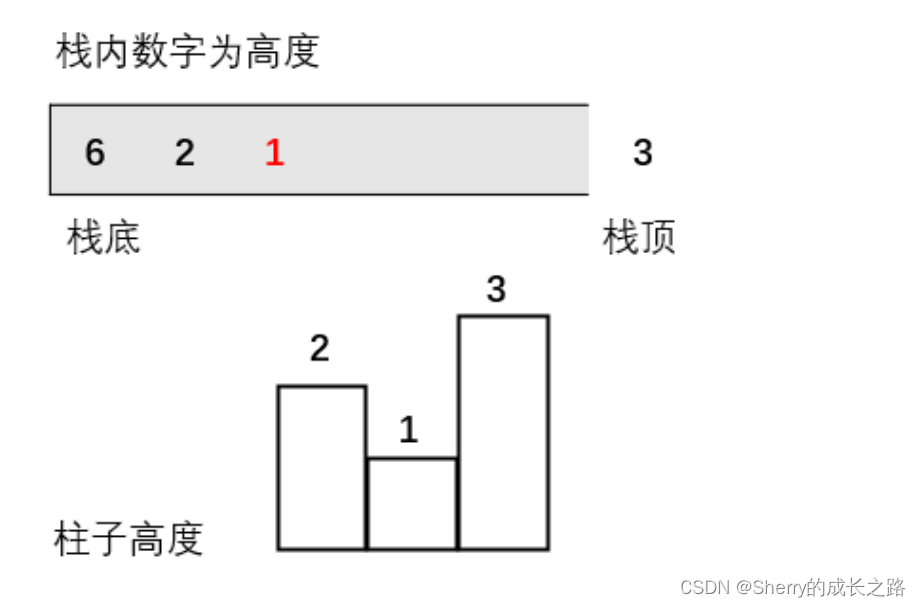
3.遇到相同高度的柱子怎么办。
遇到相同的元素，更新栈内下标，就是将栈里元素（旧下标）弹出，将新元素（新下标）加入栈中。

例如 5 5 1 3 这种情况。如果添加第二个5的时候就应该将第一个5的下标弹出，把第二个5添加到栈中。

因为我们要求宽度的时候 如果遇到相同高度的柱子，需要使用最右边的柱子来计算宽度。

如图所示：

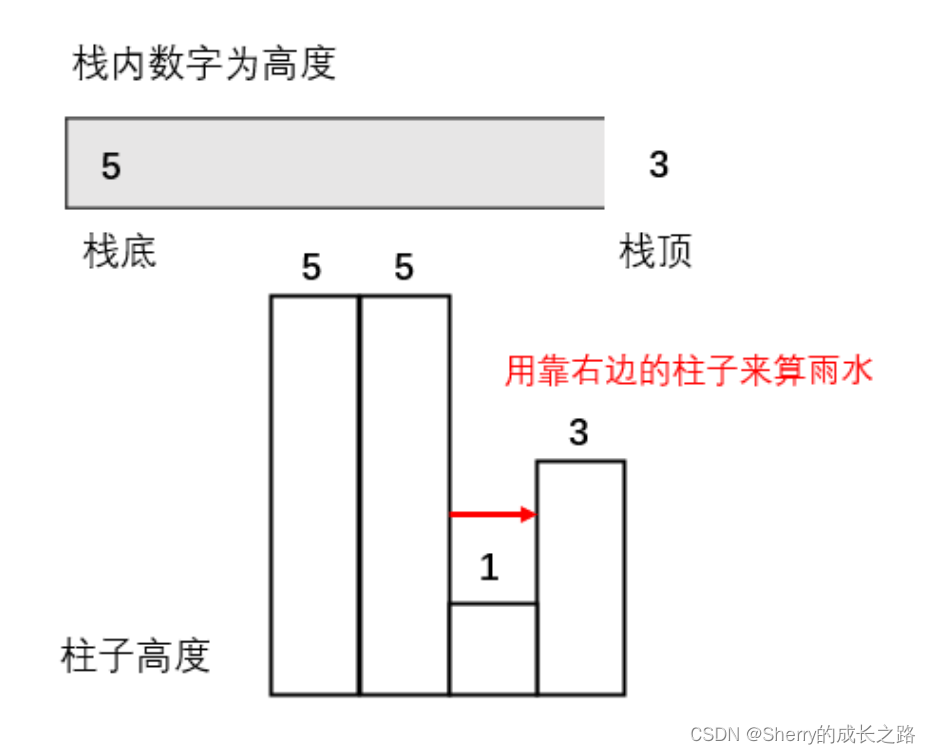
4.栈里要保存什么数值
使用单调栈，也是通过 长 * 宽 来计算雨水面积的。

长就是通过柱子的高度来计算，宽是通过柱子之间的下标来计算，

其实不用，栈里就存放下标就行，想要知道对应的高度，通过height[stack.top()] 就知道弹出的下标对应的高度了。

Deque<Integer> stack = new LinkedList<>(); // 存着下标，计算的时候用下标对应的柱子高度

明确了如上几点，我们再来看处理逻辑。

以下逻辑主要就是三种情况

情况一：当前遍历的元素（柱子）高度小于栈顶元素的高度 height[i] < height[st.top()]
情况二：当前遍历的元素（柱子）高度等于栈顶元素的高度 height[i] == height[st.top()]
情况三：当前遍历的元素（柱子）高度大于栈顶元素的高度 height[i] > height[st.top()]

先将下标0的柱子加入到栈中，st.push(0);。 栈中存放我们遍历过的元素，所以先将下标0加进来。

然后开始从下标1开始遍历所有的柱子，for (int i = 1; i < height.size(); i++)。

如果当前遍历的元素（柱子）高度小于栈顶元素的高度，就把这个元素加入栈中，因为栈里本来就要保持从小到大的顺序（从栈头到栈底）。

if (height[i] < height[stack.peek()]) {
    stack.push(i);
}

如果当前遍历的元素（柱子）高度等于栈顶元素的高度，要跟更新栈顶元素，因为遇到相相同高度的柱子，需要使用最右边的柱子来计算宽度。

}else if (height[i] == height[stack.peek()]) {
    stack.pop();
    stack.push(i);
}

如果当前遍历的元素（柱子）高度大于栈顶元素的高度，此时就出现凹槽了

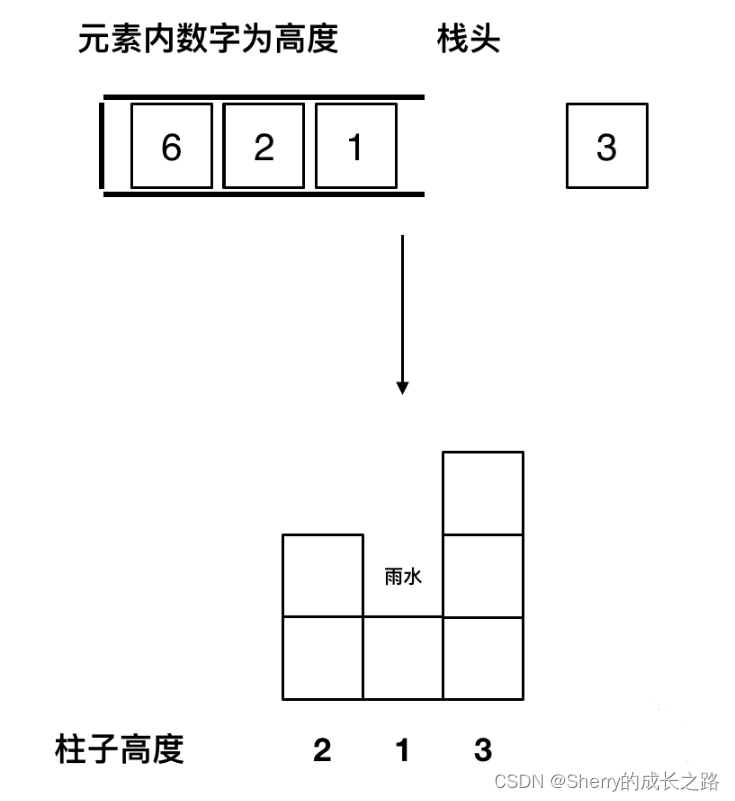
取栈顶元素，将栈顶元素弹出，这个就是凹槽的底部，也就是中间位置，下标记为mid，对应的高度为height[mid]（就是图中的高度1）。

此时的栈顶元素st.top()，就是凹槽的左边位置，下标为st.top()，对应的高度为height[st.top()]（就是图中的高度2）。

当前遍历的元素i，就是凹槽右边的位置，下标为i，对应的高度为height[i]（就是图中的高度3）。

此时大家应该可以发现其实就是栈顶和栈顶的下一个元素以及要入栈的元素，三个元素来接水！

那么雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度，代码为：int h = min(height[st.top()], height[i]) - height[mid];

雨水的宽度是 凹槽右边的下标 - 凹槽左边的下标 - 1（因为只求中间宽度），代码为：int w = i - st.top() - 1 ;

当前凹槽雨水的体积就是：h * w。

class Solution {
    public int trap(int[] height) {
        Stack<Integer> st = new Stack<>();
        st.push(0);
        int sum = 0;
        for (int i = 0; i < height.length; i++) {
            while (!st.isEmpty() && height[i] > height[st.peek()]) {
                int mid = st.pop();
                if (!st.isEmpty()) {
                    int h = Math.min(height[st.peek()], height[i]) - height[mid];
                    int w = i - st.peek() - 1;
                    sum += h * w;
                }
            }
            st.push(i);
        }
        return sum;
    }
}

总结：

今天我们完成了下一个更大元素II、接雨水两道题，相关的思想需要多复习回顾。接下来，我们继续进行算法练习。希望我的文章和讲解能对大家的学习提供一些帮助。

当然，本文仍有许多不足之处，欢迎各位小伙伴们随时私信交流、批评指正！我们下期见~