【中位数问题】两个已升序数组确定其中位数

发布时间：2023年12月25日

题目描述：?

现有两个已升序排列的数组𝐴和𝐵，其规模分别为𝑚和𝑛，试设计一个渐近时间复杂度为𝑂(log(𝑚 + 𝑛))的算法去确定𝐴和𝐵的所有元素的中位数。?

伪码：

伪码解释：?

我们把求中位数的问题转化为求两数组第k小元的问题，同时运用了二分查找来简化时间复杂度。看了网上的视频好像也没有讲得特别清晰，我们还是要结合图去看，因为时间紧张，这里就附上我的草图：

二分查找主要运用的特性就是如果两数组的第k/2个元素都相等，那很明显你们的第k/2个元素都是我的第k小元，但是如果两者不等，那肯定较小的那个和它前面比它小的元素都在我的前k个元素中，我直接把你删去然后让k缩小相同的值，好比找第7个元素，你前3个元素肯定都不是第7个元素，那我直接删去你然后我找剩下数组中的第4个元素即可

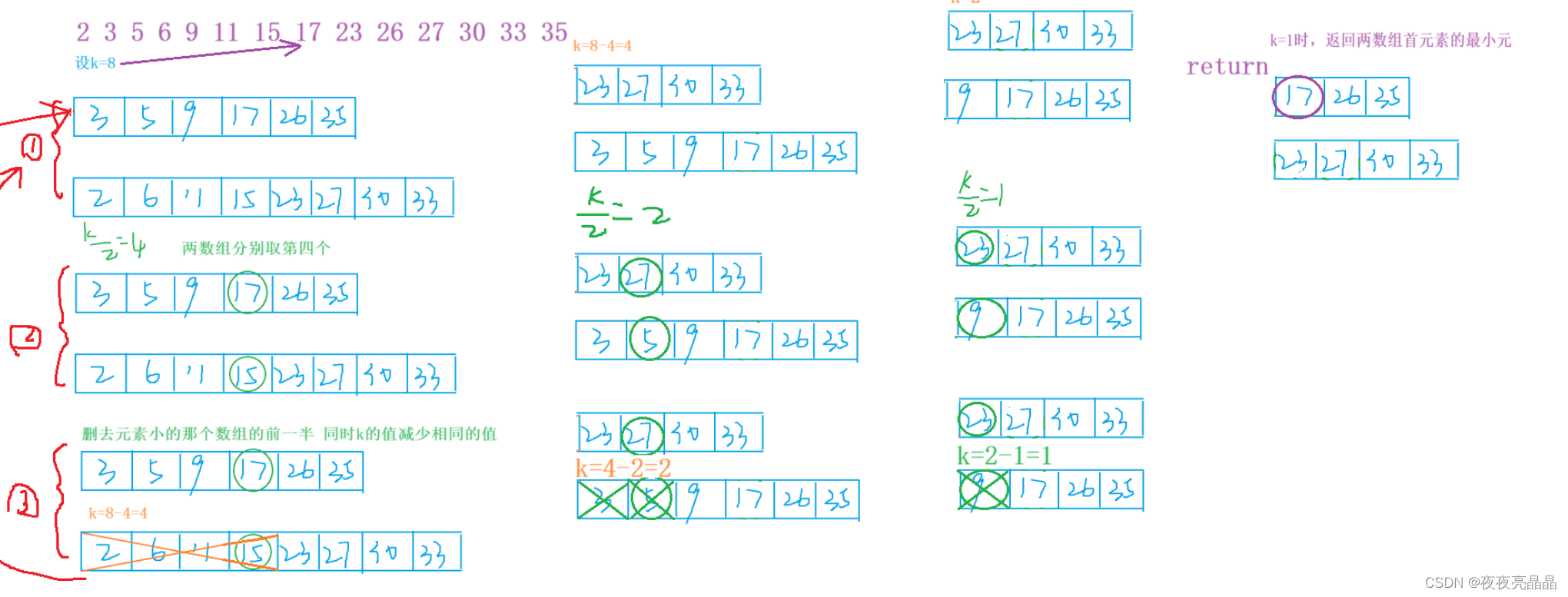这就是我草图的全部，我们现在看第一列：

其实这三步就是我们递归的思路，当我们的k逐级减少到1时，就会到达递归出口。?

文章来源:https://blog.csdn.net/m0_75186846/article/details/135193993
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章