【算法】选择最佳路线（超级源点）

?题目

有一天，琪琪想乘坐公交车去拜访她的一位朋友。

由于琪琪非常容易晕车，所以她想尽快到达朋友家。

现在给定你一张城市交通路线图，上面包含城市的公交站台以及公交线路的具体分布。

已知城市中共包含?n?个车站（编号1~n）以及?m?条公交线路。

每条公交线路都是?单向的，从一个车站出发直接到达另一个车站，两个车站之间可能存在多条公交线路。

琪琪的朋友住在?s?号车站附近。

琪琪可以在任何车站选择换乘其它公共汽车。

请找出琪琪到达她的朋友家（附近的公交车站）需要花费的最少时间。

输入格式

输入包含多组测试数据。

每组测试数据第一行包含三个整数?n,m,s，分别表示车站数量，公交线路数量以及朋友家附近车站的编号。

接下来?m?行，每行包含三个整数?p,q,t，表示存在一条线路从车站?p?到达车站?q，用时为?t。

接下来一行，包含一个整数?w，表示琪琪家附近共有?w?个车站，她可以在这?w?个车站中选择一个车站作为始发站。

再一行，包含?w?个整数，表示琪琪家附近的?w?个车站的编号。

输出格式

每个测试数据输出一个整数作为结果，表示所需花费的最少时间。

如果无法达到朋友家的车站，则输出 -1。

每个结果占一行。

数据范围

n≤1000,m≤20000
1≤s≤n
0<w<n
0<t≤1000

输入样例：

5 8 5
1 2 2
1 5 3
1 3 4
2 4 7
2 5 6
2 3 5
3 5 1
4 5 1
2
2 3
4 3 4
1 2 3
1 3 4
2 3 2
1
1

输出样例：

1
-1

思路

?本题是一道很经典的超级源点的题目，琪琪可以从多个点出发，到达点s，如下图所示：

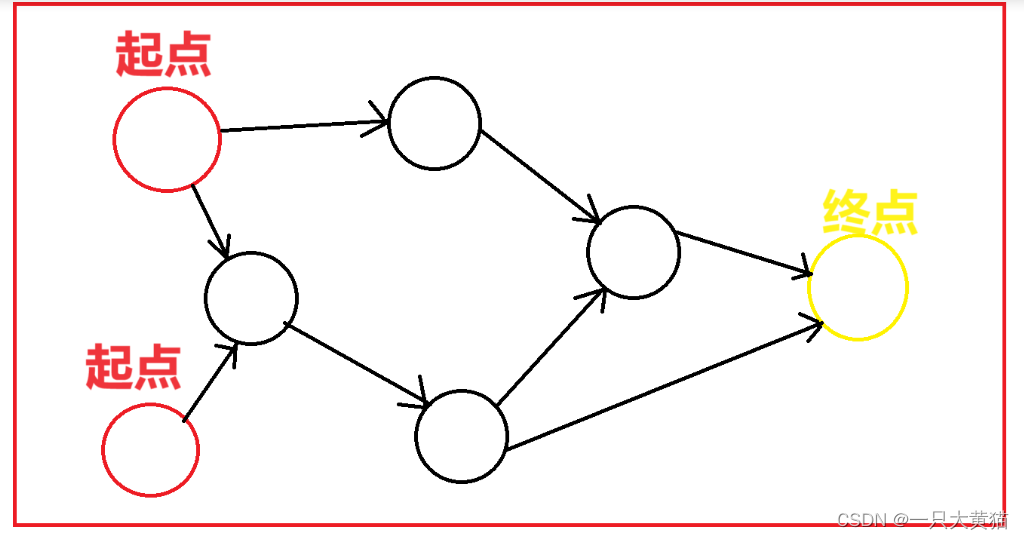
但是如果从每个起点都出发一次做dijkstra算法，问题会变得十分复杂，且时间复杂度会很高，不如建立一个超级源点，超级源点连接所有起点，如下如所示：

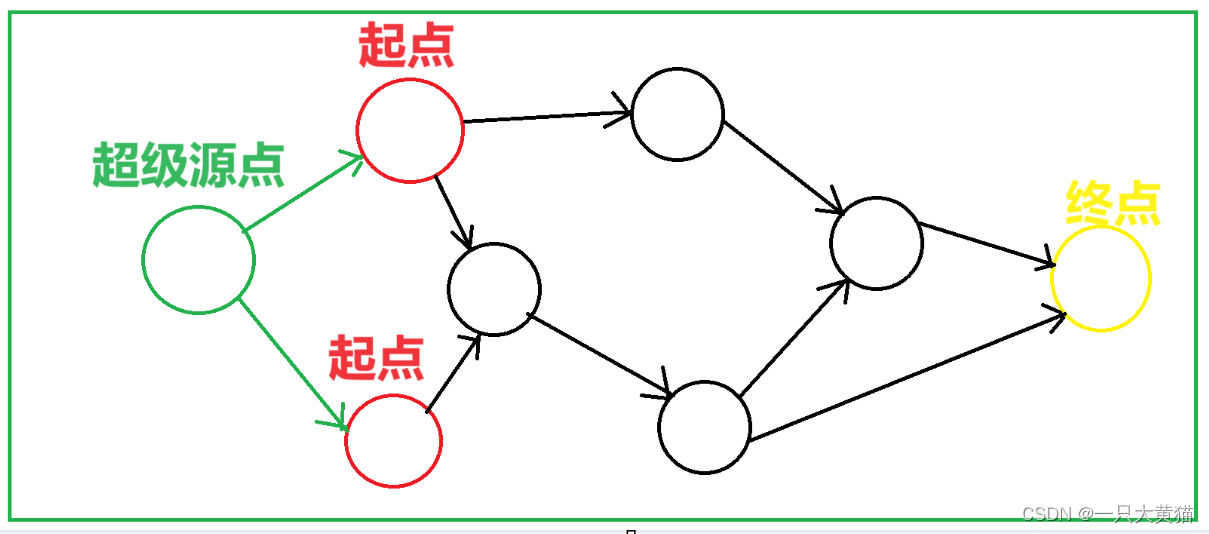
超级源点建立完成之后，可以从超级源点出发做一次dijkstra算法即可求出从所有起点出发到达终点的最小路径长度。?

代码?

#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10,M = 2e4 + 10;
typedef pair<int,int> PII;
priority_queue<PII,vector<PII>,greater<>> heap;
int n,m,s;
int W;
int dist[N];
int h[N],ne[M],e[M],w[M],idx;
bool st[N];

void add(int a,int b,int c)
{
    ne[idx] = h[a],e[idx] = b,w[idx] = c,h[a] = idx ++;
}

void dijkstra()
{
    while(!heap.empty())
    {
        auto t = heap.top();
        heap.pop();
        int y = t.second;
        if(st[y]) continue;
        st[y] = true;
        for(int i = h[y]; ~i; i = ne[i])
        {
            int j = e[i];
            if(dist[j] > dist[y] + w[i])
            {
                dist[j] = dist[y] + w[i];
                heap.emplace(dist[j],j);
            }
        }
    }
}

void solve()
{
    memset(st,0,sizeof st);
    memset(dist,0x3f,sizeof dist);
    memset(h,-1,sizeof h);
    idx = 0;
    while(m --)
    {
        int a,b,c;
        cin >> a >> b >> c;
        add(a,b,c);
    }
    cin >> W;
    while(W --)
    {
        int a;
        cin >> a;
        dist[a] = 0;
        heap.emplace(0,a);
    }
    dijkstra();
    if(dist[s] >= 0x3f3f3f3f) cout << -1 << endl;
    else cout << dist[s] << endl;
}

int main()
{
    while(scanf("%d%d%d",&n,&m,&s) != -1) solve();
    return 0;
}

难度：简单

时/空限制：1s / 64MB

总通过数：7200

总尝试数：15733

来源：HDOJ

算法标签 最短路

题目来自:1137. 选择最佳线路 - AcWing题库?