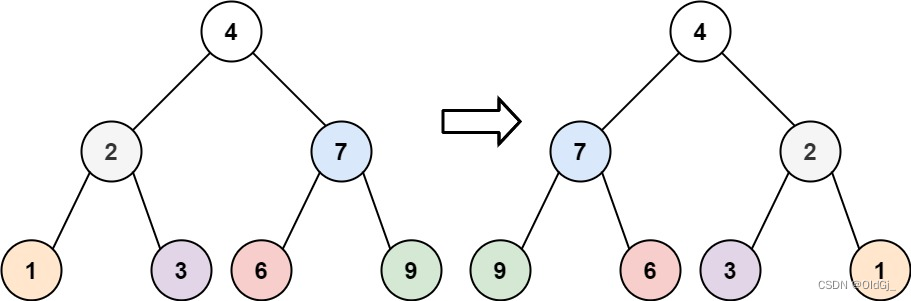
【算法提升】LeetCode每五日一总结【01/01--01/05】

LeetCode每五日一总结【01/01–01/05】

这次总结额外加上2023年最后一天2023/12/31日的题目，总共六天！

2023/12/31

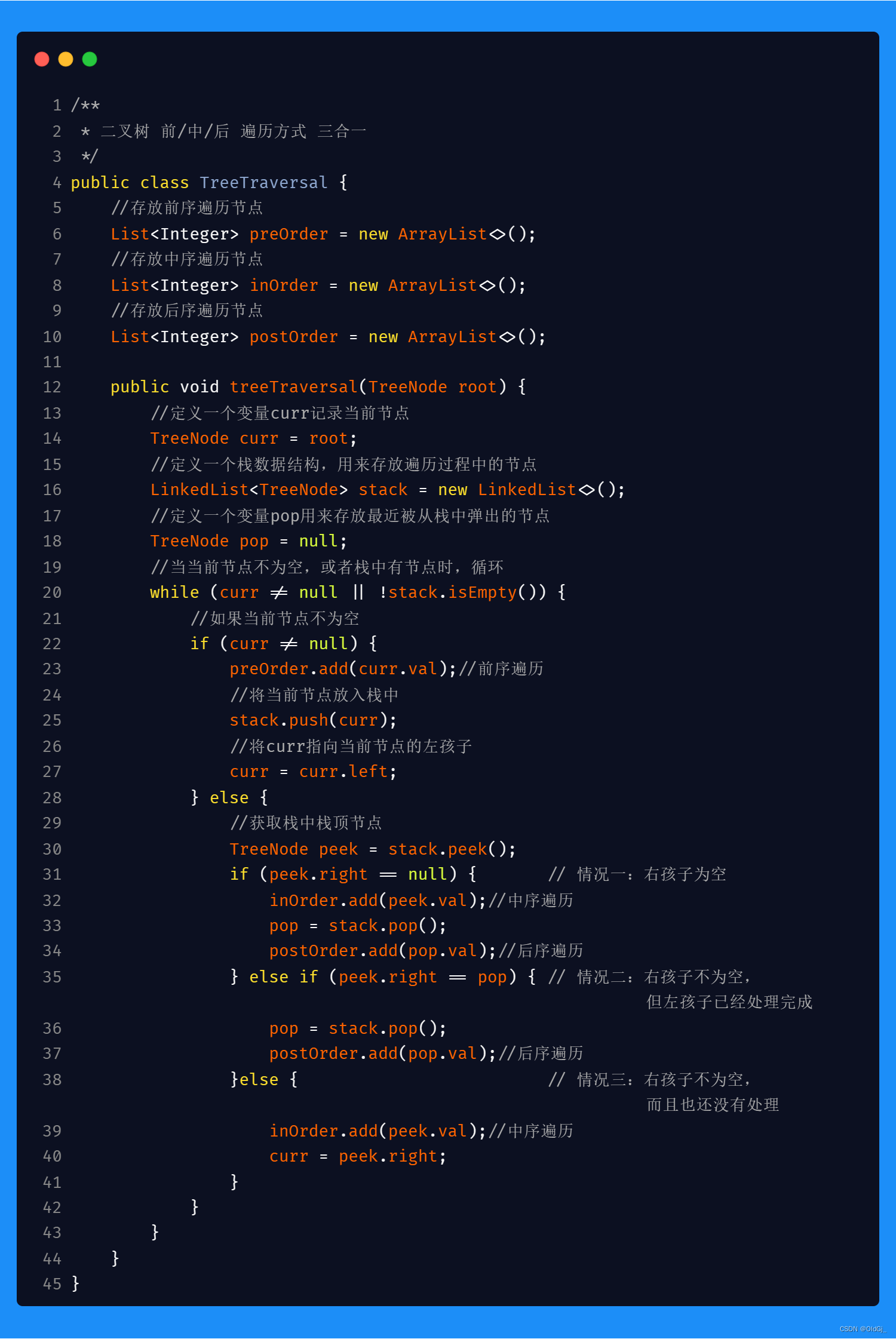
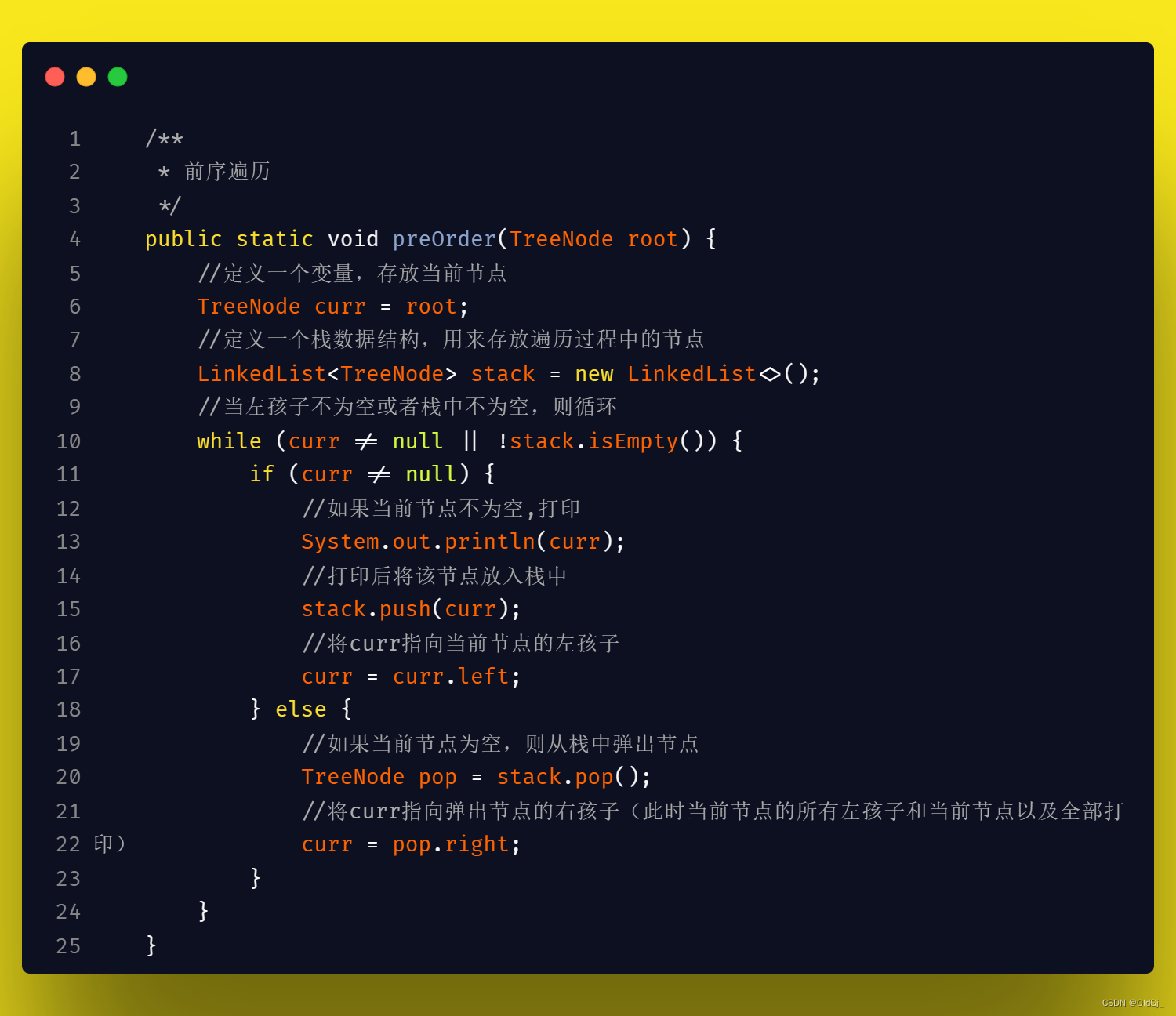
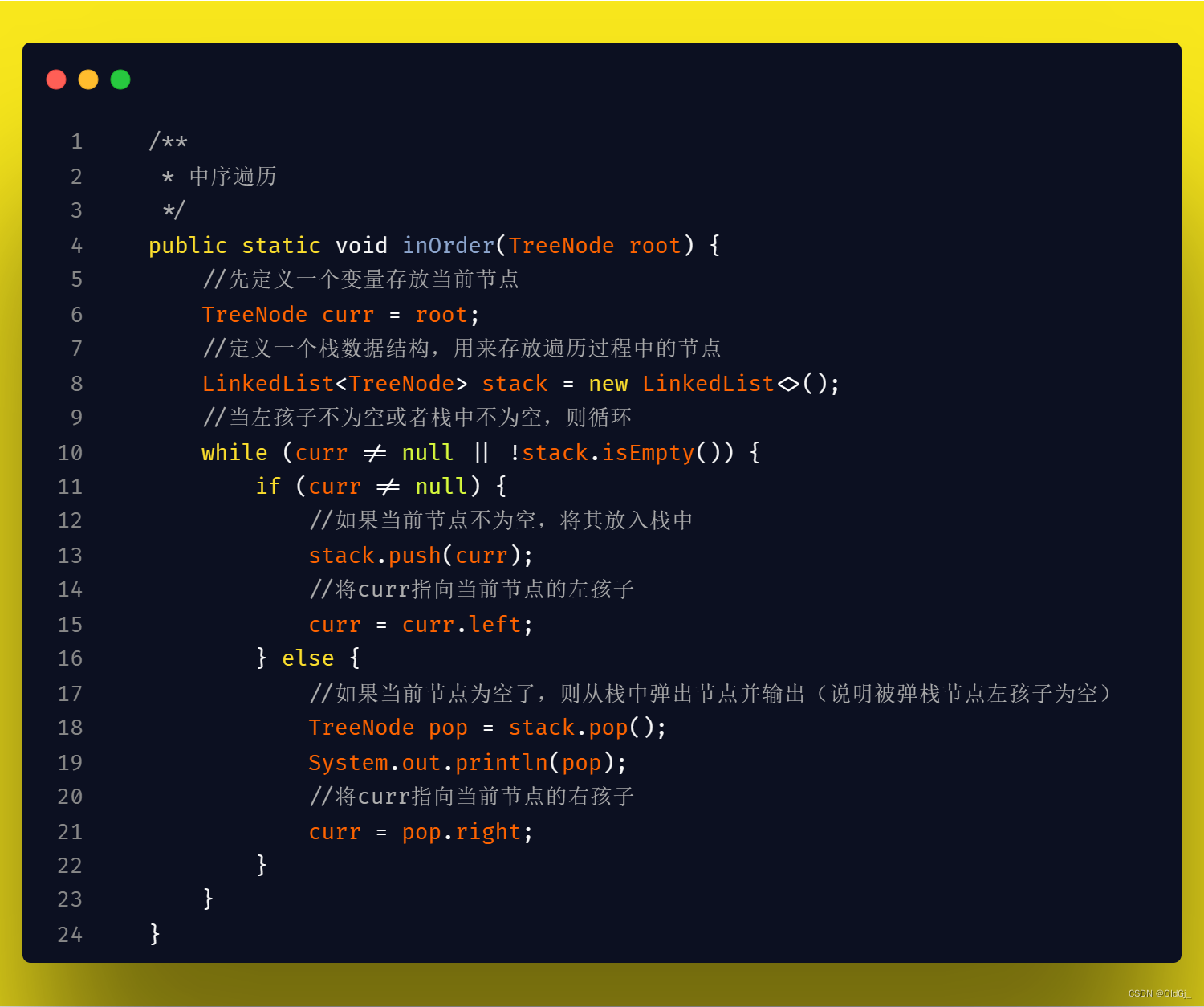
二叉树的前/中/后 序遍历<非递归>

使用非递归方式实现二叉树的前/中/后序遍历，最终要的思想是需要用到栈这样的数据结构，因为我们需要在遍历的过程中，时刻记着返回的路，以便我们遍历完一颗子树后，可以返回回来遍历其他子树：

? 具体的，前序遍历时，需要在当前节点不为空时就直接操作当前节点，待操作完成后，再将当前节点入栈并且指向当前节点的左孩子，循环该操作，直到当当前节点为空，则开始准备返回，此时从栈中pop节点，并判断pop出的节点是否有右孩子，如果有，则将右孩子赋值给当前节点，继续上面的操作即可。

? 中序遍历的代码思想和前序遍历是非常类似的，只是在操作节点的时机上有所不同，前序遍历是在当节点不为空时直接操作节点，而中序遍历则需要在当前节点为空后，从栈中pop出第一个元素时，操作pop出的元素，因为此时pop出的元素已经没有左孩子。

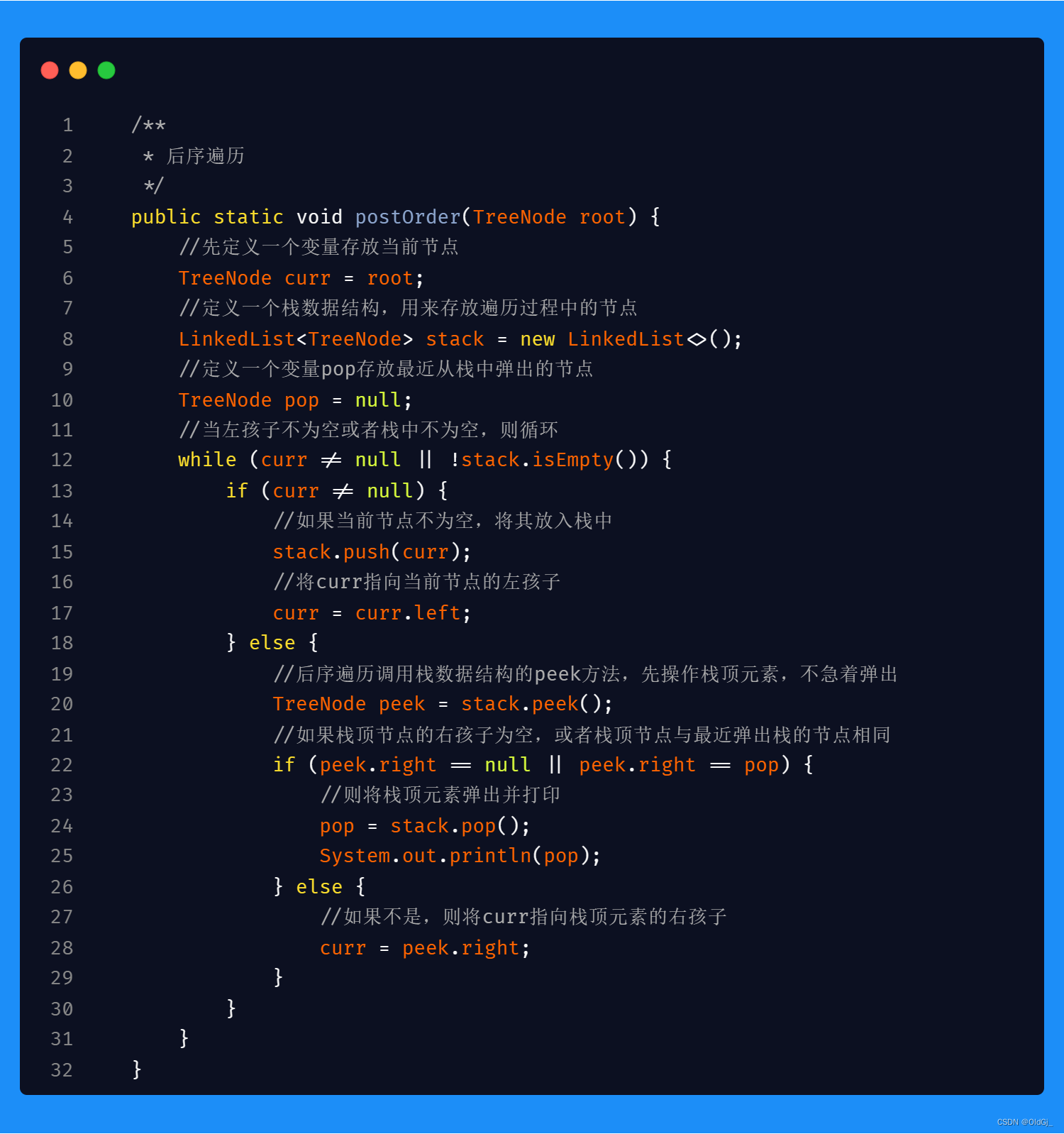
? 后序遍历的代码和前序遍历及中序遍历有所区别，最大的区别在于，当当前节点为空时，我们不能立刻从栈顶pop节点并操作该节点，而应该先判断栈顶元素节点的右孩子没有或者已经被操作，那么判断栈顶节点右孩子为空很容易，如何判断栈顶节点右孩子是否被操作过呢？此时，我们可以定义一个变量pop记录最近一次被pop出的节点，如果栈顶元素的右孩子和记录的pop变量中的节点是同一个节点，则说明栈顶元素的右孩子以及被操作，此时即可pop出栈顶节点进行操作。如果不是同一个节点，则将说明栈顶元素有右孩子而且暂时没有被操作，此时要将右孩子赋值给当前节点，重复以上判断。

2024/01/01

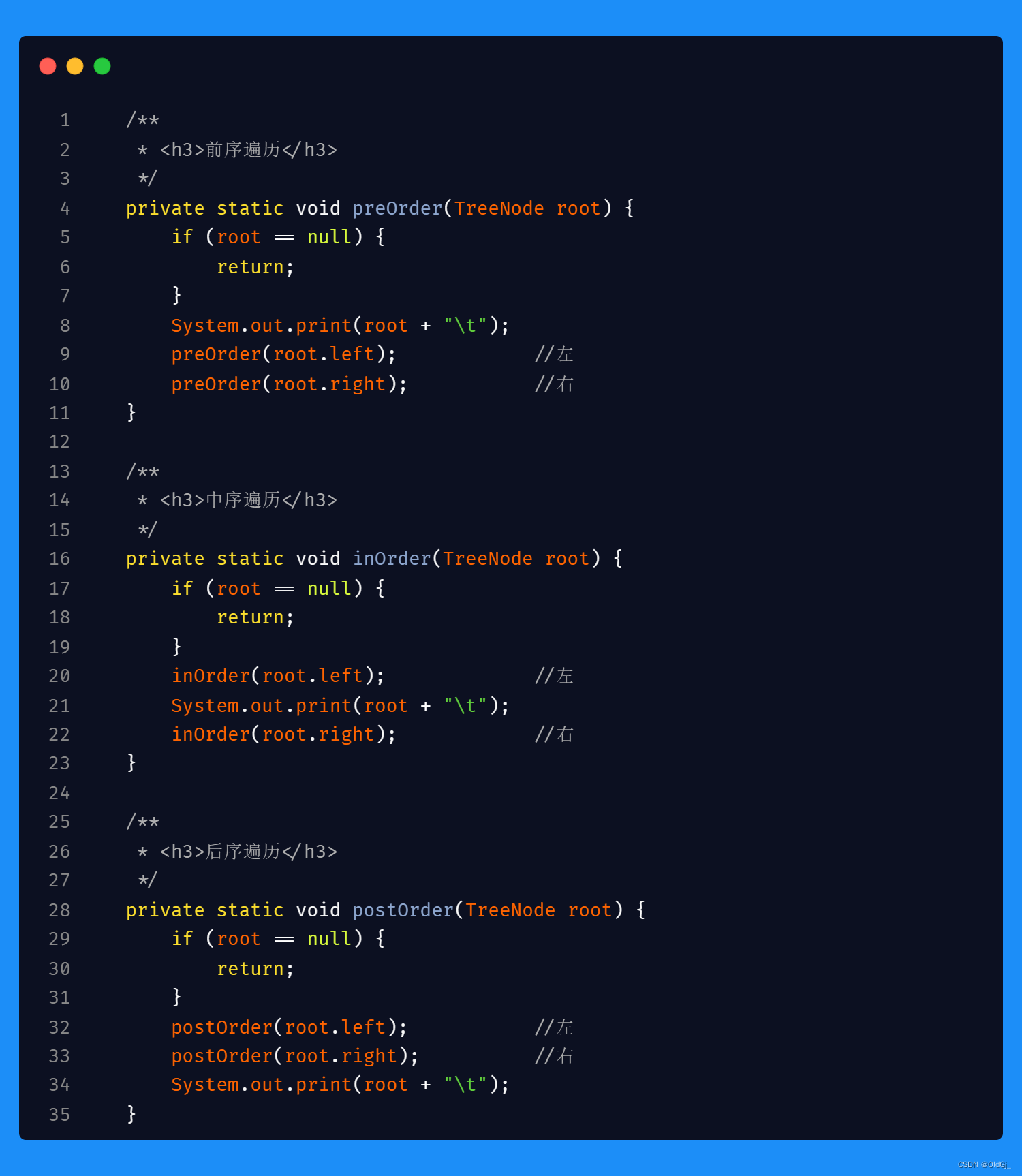
二叉树的 前/中/后 序遍历 三合一代码<非递归>

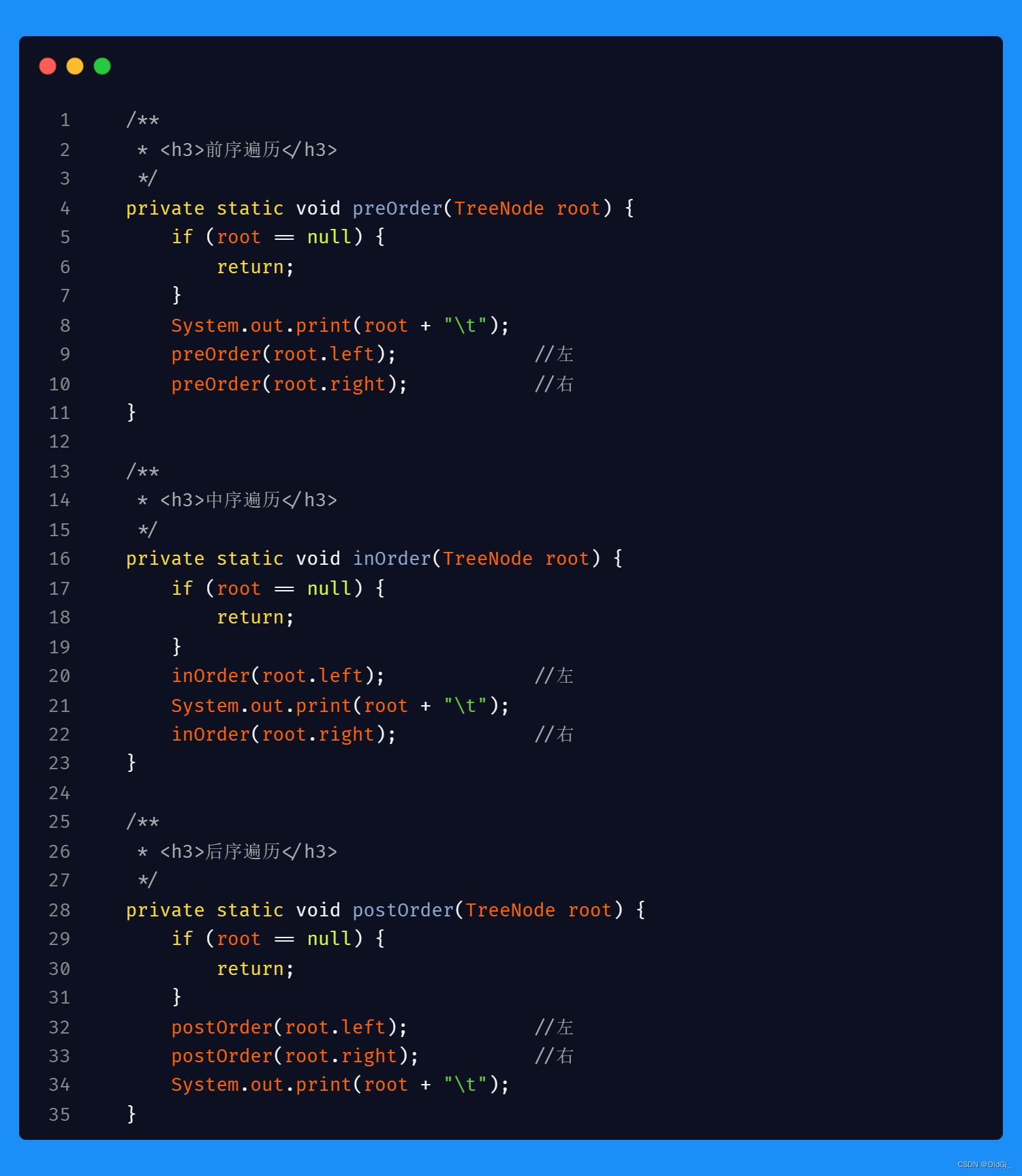
所谓三合一代码，就是将之前分开写的三段递归代码，合在一段代码中，在代码的不同时机，进行不同的节点操作即可实现一段代码进行了前/中/后三次遍历的效果，有助于进一步理解二叉树的三种遍历方式，不同点在于操作栈中的节点，大家可以重点关注：

?

二叉树的 前/中/后 序遍历 三合一代码<递归>

递归实现二叉树的遍历代码很简单易懂，附上代码，不过多赘述：

?

2024/01/02

101. 对称二叉树

这道题判断一个二叉树是否是对称的，我们可以想到判断根节点的左右孩子是否是对称的，其他节点的判断方法和根节点相同，很容易想到采用递归方法，因此，在check方法中定义好判断条件（

1. 如果left和right都为空，返回true，因为它们都是空的。
2. 如果left或right为空，返回false，因为其中一个树不是空的。
3. 如果left和right的值不相等，返回false，因为树不是对称的。

）后，只需递归（左孩子的左孩子和右孩子的右孩子为参数）调用该方法，即可判断整颗树是否为对称树

2024/01/03

104. 二叉树的最大深度

方法一：后序遍历递归法

1. 判断根节点是否为空，如果是，则返回0，因为深度为0。
2. 如果根节点的左右子节点都为空，说明该节点没有子节点，返回1，因为深度为1。
3. 否则，递归地计算左子树和右子树的深度，分别存储在maxLeft和maxRight变量中。
4. 最后，将maxLeft和maxRight中的最大值加1，得到本节点的最大深度，并返回。

关于深度的定义：从根节点出发，离根节点最远的节点所经过的边数，即该节点的深度。注意，这里的深度定义与力扣上的默认定义略有不同，深度为0表示没有节点，深度为1表示有一个根节点，深度为2表示有一个根节点和一个子节点，以此类推。

方法二：后序遍历非递归法

非递归法实现二叉树的后序遍历时，需要使用到栈数据结构，用于记录遍历一颗子树完成后返回的路，此时，如果是后序遍历，只有遍历到叶子节点时才会从栈中pop元素，因此，栈中最大的元素个数就对应着二叉树的最大深度，我们只需要在向栈中放入元素方法后面，记录栈中元素个数，返回最大的元素个数即可。

方法三：层序遍历

使用层序遍历计算二叉树的最大深度，我们只需要定义一个记录深度的变量，在遍历完每一层的所有节点后，该变量＋1即可。

111. 二叉树的最小深度

方法一：二叉树的最小深度<递归>

思路：当根节点没有左右孩子，则返回最小深度为1，当根节点只有左孩子，则递归调用求出左孩子的最小深度+1即可，相同的，如果根节点只有右孩子，则递归调用求出右孩子的最小深度+1即可；

对于一个非空节点，如果它的左子节点和右子节点都为空，那么它的最小深度为1；****如果它的左子节点为空，那么它的最小深度为右子节点的最小深度加1；如果它的右子节点为空，那么它的最小深度为左子节点的最小深度加1；****否则，它的最小深度为左右子节点最小深度的较小值加1。

1. 如果根节点为空，则返回0。
2. 如果根节点的左子节点和右子节点都为空，则返回1。
3. 如果根节点的左子节点为空，则返回根节点的右子节点的最小深度加1。
4. 如果根节点的右子节点为空，则返回根节点的左子节点的最小深度加1。
5. 否则，返回左右子节点最小深度的较小值加1。

方法二：二叉树的最小深度<层序遍历>??（效率更优）

核心思想：当层序遍历找到第一个叶子节点时，返回第一个叶子节点所在层数即为最小深度。

#注意：应当在循环遍历每一层节点之前，先将层数+1，此时的层数变量才表示当前层

2024/01/04

226. 翻转二叉树

主要逻辑：

1. 如果当前节点为空，则返回，因为不需要对空节点进行反转。
2. 定义一个节点对象 t，用于充当中间过渡节点，先将左子树赋值给中间节点。
3. 将右子树赋值给左子树节点。
4. 将中间节点中存放的左子树赋值给右子树，完成根节点的左右子树反转。
5. 递归调用 fn 方法，将根节点的左孩子的孩子节点反转。
6. 将根节点的右孩子的孩子节点反转。

2024/01/05

105. 从前序与中序遍历序列构造二叉树

主要逻辑：

1. 如果输入的数组为空，则返回空。
2. 取前序遍历数组的第一个元素作为根节点的值。
3. 遍历中序遍历数组，找到根节点所在位置。
4. 根据根节点的位置，将中序遍历数组分为左部分和右部分，其中左部分即为根节点左子树的中序遍历数组，右部分即为根节点右子树的中序遍历数组。
5. 根据左部分和中序遍历数组左部分的个数，将前序遍历数组从第二个元素开始分为左部分和右部分，其中左部分即为根节点左子树的前序遍历数组，右部分即为根节点右子树的前序遍历数组。
6. 分别递归地构造根节点的左子树和右子树，并将它们分别作为根节点的左子树节点和右子树节点。
7. 返回根节点。

106. 从中序与后序遍历序列构造二叉树

主要逻辑：

1. 如果输入的数组为空，则返回空。
2. 取后序遍历数组的最后一个元素作为根节点的值。
3. 遍历中序遍历数组，找到根节点所在位置。
4. 根据根节点的位置，将中序遍历数组分为左部分和右部分，其中左部分即为根节点左子树的中序遍历数组，右部分即为根节点右子树的中序遍历数组。
5. 根据左部分和中序遍历数组左部分的个数，将后序遍历数组从第一个元素开始分为左部分和右部分，其中左部分即为根节点左子树的后序遍历数组，右部分即为根节点右子树的后序遍历数组。
6. 分别递归地构造根节点的左子树和右子树，并将它们分别作为根节点的左子树节点和右子树节点。
7. 返回根节点。

2023/12/31

今日数据结构：二叉树的前/中/后 序遍历<非递归>

前序遍历：

中序遍历：

后序遍历：

2024/01/01

今日数据结构：二叉树的 前/中/后 序遍历 三合一代码<非递归>

今日数据结构：二叉树的 前/中/后 序遍历 三合一代码<递归>

2024/01/02

每日力扣：101. 对称二叉树

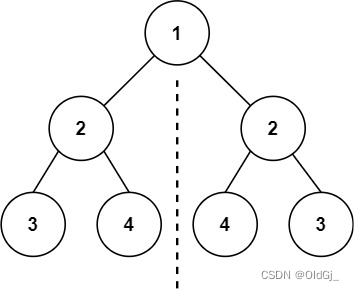
给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

?

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

?

输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

• 树中节点数目在范围 [1, 1000] 内
• -100 <= Node.val <= 100

**进阶：**你可以运用递归和迭代两种方法解决这个问题吗？

	public boolean isSymmetric(TreeNode root) {
        return check(root.left, root.right);
    }

    private boolean check(TreeNode left, TreeNode right) {
        if (left == null && right == null) {
            return true;
        }
        if (left == null || right == null) {
            return false;
        }
        if (left.val != right.val) {
            return false;
        }
        return check(left.left, right.right) && check(left.right, right.left);
    }

这段Java代码定义了一个名为isSymmetric的方法，该方法接受一个TreeNode对象作为输入并返回一个布尔值。该方法检查以root为根的树是否对称。

check是一个私有辅助方法，它接受两个TreeNode对象作为输入并返回一个布尔值。它通过比较两个树的根值并递归地检查它们的左和右子树是否对称来检查两个树是否对称。

isSymmetric方法的逻辑如下：

1. 如果left和right都为空，返回true，因为它们都是空的。
2. 如果left或right为空，返回false，因为其中一个树不是空的。
3. 如果left和right的值不相等，返回false，因为树不是对称的。
4. 如果left和right的值相等，调用check方法对left和right的左和右子树进行递归比较，并返回结果。

isSymmetric方法返回true，如果树是对称的，否则返回false。

2024/01/03

每日力扣：104. 二叉树的最大深度

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

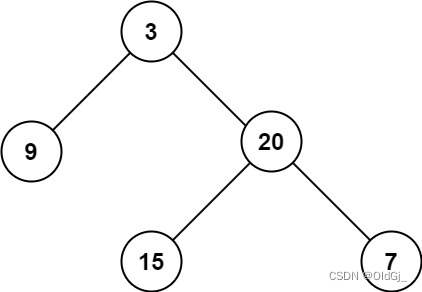
示例 1：

?

输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

• 树中节点的数量在 [0, 104] 区间内。
• -100 <= Node.val <= 100

/**
 * 求树的最大深度<后序遍历-递归>
 */
public class Leetcode104_1 {

    /*
    思路：
    1. 得到左子树深度, 得到右子树深度, 二者最大者加一, 就是本节点深度
    2. 因为需要先得到左右子树深度, 很显然是后序遍历典型应用
    3. 关于深度的定义：从根出发, 离根最远的节点总边数,
        注意: 力扣里的深度定义要多一

        深度2         深度3         深度1
        1            1            1
       / \          / \
      2   3        2   3
                        \
                         4
    */
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        if (root.left == null && root.right == null) {
            return 1;
        }
        //得到左子树深度
        int maxLeft = maxDepth(root.left);
        //得到右子树深度
        int maxRight = maxDepth(root.right);
        //二者最大者加一, 就是本节点深度
        return Integer.max(maxLeft, maxRight) + 1;
    }
}

方法一：求树的最大深度**<后序遍历-递归>** ??

? 利用递归方法，逻辑是

1. 得到左子树深度, 得到右子树深度, 二者最大者加一, 就是本节点深度
2. 因为需要先得到左右子树深度, 很显然是后序遍历典型应用

要求先操作左右子树的题目，可以想到后序遍历。

这段Java代码是Leetcode上的第104题的解法。题目要求给定一个二叉树，返回其最大深度。

首先，定义了一个名为Leetcode104_1的类，其中包含一个名为maxDepth的方法，该方法接受一个Tree Node类型的参数，表示二叉树的根节点。

maxDepth方法的主要思路如下：

1. 判断根节点是否为空，如果是，则返回0，因为深度为0。
2. 如果根节点的左右子节点都为空，说明该节点没有子节点，返回1，因为深度为1。
3. 否则，递归地计算左子树和右子树的深度，分别存储在maxLeft和maxRight变量中。
4. 最后，将maxLeft和maxRight中的最大值加1，得到本节点的最大深度，并返回。

关于深度的定义：**从根节点出发，离根节点最远的节点所经过的边数，即该节点的深度。**注意，这里的深度定义与力扣上的默认定义略有不同，深度为0表示没有节点，深度为1表示有一个根节点，深度为2表示有一个根节点和一个子节点，以此类推。

总之，这段代码的主要目的是通过递归地计算左右子树的深度，然后找到它们中的最大值，最后将该最大值加1，得到本节点的最大深度。

/**
 * 求二叉树的最大深度<后序遍历-非递归>
 */
public class Leetcode104_2 {
    public int maxDepth(TreeNode root) {
        TreeNode curr = root;
        //非递归方法遍历树需要栈数据结构
        LinkedList<TreeNode> stack = new LinkedList<>();
        //非递归法实现后序遍历需要定义一个指针记录最近一次从栈中弹出的元素
        TreeNode pop = null;
        //记录最大深度
        int max = 0;
        while (curr != null || !stack.isEmpty()) {
            if (curr != null) {
                stack.push(curr);
                //在向栈中添加元素后，栈中元素个数发生改变，栈中最大元素个数就是树的最大深度
                int size = stack.size();
                if (size > max) {
                    max = size;
                }
                curr = curr.left;
            } else {
                TreeNode peek = stack.peek();
                if (peek.right == null || peek.right == pop) {
                    pop = stack.pop();
                } else {
                    curr = peek.right;
                }
            }
        }
        return max;
    }
}

方法二 ：求二叉树的最大深度**<后序遍历-非递归>**

这段Java代码是Leetcode上的第104题的另一个解法。题目要求给定一个二叉树，返回其最大深度。

与上一个解法不同，这个解法使用了非递归的方法遍历二叉树。在遍历过程中，使用一个栈来存储当前节点及其路径上的节点，同时记录栈中的最大元素个数，即为二叉树的最大深度。

具体实现如下：

1. 初始化一个栈，一个用于记录最大深度的变量max，以及一个用于记录最近一次出栈节点的变量pop。
2. 如果当前节点不为空，则将当前节点入栈，并将栈中元素个数与当前最大深度进行比较，如果栈中元素个数大于当前最大深度，则更新最大深度。
3. 如果当前节点为空，则将栈顶节点出栈，如果栈顶节点的右子节点为空或者右子节点已经被访问过（即与pop相等），则将栈顶节点出栈，否则将右子节点入栈。
4. 重复步骤2和3，直到栈为空。
5. 返回最大深度。

这个解法的时间复杂度为O(n)，空间复杂度为O(n)，其中n为二叉树的节点个数。

/**
 * 二叉树的最大深度<层序遍历>
 */
@SuppressWarnings("all")
public class Leetcode104_3 {

    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        //二叉树的层序遍历需要用到队列数据结构
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        //记录深度
        int depth = 0;
        while (!queue.isEmpty()) {
            //每一层节点个数<队列中元素个数记录的就是每一层节点的个数>
            int size = queue.size();
            //当前层有多少节点就循环多少次
            for (int i = 0; i < size; i++) {
                //就把多少节点从队列中弹出，并把它们的孩子加入队列
                TreeNode pollNode = queue.poll();
                if (pollNode.left != null) {
                    queue.offer(pollNode.left);
                }
                if (pollNode.right != null) {
                    queue.offer(pollNode.right);
                }
            }
            //每循环一层，层数 + 1
            depth++;
        }
        //当循环完所有节点，返回层数
        return depth;
    }
}

方法三：二叉树的最大深度**<层序遍历>**

与上一个解法不同，这个解法使用了二叉树的层序遍历方法。在遍历过程中，记录每一层的节点个数，当遍历完一层后，将深度加1，直到队列为空，此时的深度即为二叉树的最大深度。

具体实现如下：

1. 如果根节点为空，则返回0。
2. 初始化一个队列，用于存储二叉树的节点，并将根节点入队。
3. 初始化一个深度变量depth，用于记录二叉树的层数。
4. 当队列不为空时，进入循环：
   a. 计算队列中的节点个数size，用于表示当前层的节点个数。
   b. 循环size次，表示当前层有size个节点：
   i. 从队列中弹出一个节点pollNode。
   ii. 如果pollNode的左子节点不为空，则将左子节点入队。
   iii. 如果pollNode的右子节点不为空，则将右子节点入队。
   c. 每循环一次，表示当前层遍历完毕，将深度加1。
5. 当队列为空时，跳出循环，返回深度变量depth。

这个解法的时间复杂度为O(n)，空间复杂度为O(n)，其中n为二叉树的节点个数。

每日力扣：111. 二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

**说明：**叶子节点是指没有子节点的节点。

示例 1：

?

输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

• 树中节点数的范围在 [0, 105] 内
• -1000 <= Node.val <= 1000

/**
 * 二叉树的最小深度<b><递归></b>
 */
public class Leetcode111_1 {
    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int minLeft = minDepth(root.left);
        int minRight = minDepth(root.right);
        if (minRight == 0) {
            return minLeft + 1;
        }
        if (minLeft == 0) {
            return minRight + 1;
        }
        return Integer.min(minLeft, minRight) + 1;
    }
}

方法一：二叉树的最小深度**<递归>**

这段Java代码是Leetcode上的第111题的另一个解法。题目要求给定一个二叉树，返回其最小深度。

与上一个解法不同，这个解法使用了递归的方法。对于一个非空节点，如果它的左子节点和右子节点都为空，那么它的最小深度为1；****如果它的左子节点为空，那么它的最小深度为右子节点的最小深度加1；如果它的右子节点为空，那么它的最小深度为左子节点的最小深度加1；****否则，它的最小深度为左右子节点最小深度的较小值加1。

具体实现如下：

1. 如果根节点为空，则返回0。
2. 如果根节点的左子节点和右子节点都为空，则返回1。
3. 如果根节点的左子节点为空，则返回根节点的右子节点的最小深度加1。
4. 如果根节点的右子节点为空，则返回根节点的左子节点的最小深度加1。
5. 否则，返回左右子节点最小深度的较小值加1。

这个解法的时间复杂度为O(n)，空间复杂度为O(n)，其中n为二叉树的节点个数。

/**
 * 二叉树的最小深度<b><层序遍历></b>
 */
@SuppressWarnings("all")
public class Leetcode111_2 {
    public int minDepth(TreeNode root) {
        if(root==null){
            return 0;
        }
        //思想：使用层序遍历，当遍历到第一个叶子节点，他所在的层就是最小深度
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int Depth = 0;
        while (!queue.isEmpty()) {
            Depth++;
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode poll = queue.poll();
                //判断是否是叶子节点
                if(poll.right==null&&poll.left==null){
                    //如果是，则直接返回当前节点的层数即为深度
                    return Depth;
                }
                if (poll.left != null) {
                    queue.offer(poll.left);
                }
                if (poll.right != null) {
                    queue.offer(poll.right);
                }
            }
        }
        return Depth;
    }
}

方法二：二叉树的最小深度****<层序遍历>****??

? 核心思想： 使用层序遍历，当遍历到第一个叶子节点，他所在的层就是最小深度

这段代码是用于计算二叉树的最小深度。它使用了一种叫做"层序遍历"的方法来解决这个问题。

首先，如果根节点为空，那么深度为0。

然后，创建一个队列来存储每一层的节点。将根节点加入队列中，并将深度设为1。

接下来，进入一个while循环，只要队列不为空，就执行以下操作：

1. 将当前深度加1。
2. 计算队列的大小，表示当前层的节点数量。
3. 遍历当前层的节点，将它们从队列中移出，并判断它们是否是叶子节点（即没有左右子节点）。
4. 如果找到第一个叶子节点，直接返回当前节点的深度，即为最小深度。
5. 如果当前节点的左右子节点都不为空，将它们加入队列中。

当while循环结束时，说明所有节点都已经遍历过了，但仍然没有找到叶子节点，那么二叉树的最小深度就是最后那层的深度。

2024/01/04

每日力扣：226. 翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目范围在 [0, 100] 内
• -100 <= Node.val <= 100

/**
 * 反转二叉树
 */
public class Leetcode226 {
    public TreeNode invertTree(TreeNode root) {
        //反转方法
        fn(root);
        return root;
    }
	
    private void fn(TreeNode node) {
        //结束递归条件：如果节点为空，返回
        if (node == null) {
            return;
        }
        //定义一个节点对象，用于充当中间过渡节点，先将左子树赋值给中间节点
        TreeNode t = node.left;
        //将右子树赋值给左子树节点
        node.left = node.right;
        //再将中间节点中存放的左子树赋值给右子树，完成根节点的左右子树反转
        node.right = t;
        //递归调用反转方法，将根节点的左孩子的孩子节点反转
        fn(node.left);
        //将根节点的右孩子的孩子节点反转
        fn(node.right);
    }
}

这段代码定义了一个名为 Leetcode226 的类，它包含一个名为 invertTree 的方法，该方法接受一个二叉树的根节点作为参数，并返回反转后的二叉树的根节点。

该方法首先调用一个名为 fn 的私有方法，该方法用于递归地反转二叉树的左右子树。

fn 方法的主要逻辑如下：

1. 如果当前节点为空，则返回，因为不需要对空节点进行反转。
2. 定义一个节点对象 t，用于充当中间过渡节点，先将左子树赋值给中间节点。
3. 将右子树赋值给左子树节点。
4. 将中间节点中存放的左子树赋值给右子树，完成根节点的左右子树反转。
5. 递归调用 fn 方法，将根节点的左孩子的孩子节点反转。
6. 将根节点的右孩子的孩子节点反转。

最后，invertTree 方法将反转后的二叉树的根节点返回。

2024/01/05

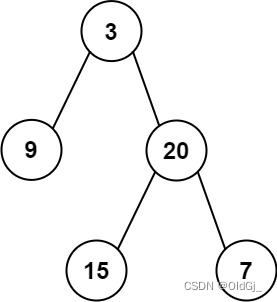
每日力扣：105. 从前序与中序遍历序列构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

?

输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

• 1 <= inorder.length <= 3000
• postorder.length == inorder.length
• -3000 <= inorder[i], postorder[i] <= 3000
• inorder 和 postorder 都由 不同 的值组成
• postorder 中每一个值都在 inorder 中
• inorder 保证是树的中序遍历
• postorder 保证是树的后序遍历

public class Leetcode105 {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        /*
            输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
            输出: [3,9,20,null,null,15,7]
        */
        
        //结束递归的条件：当遍历数组为空时，说明已经没有值，返回空
        if (preorder.length == 0) {
            return null;
        }

        // 前序遍历的第一个值一定是根节点的值
        int rootValue = preorder[0];
        //创建根节点
        TreeNode root = new TreeNode(rootValue);
        //遍历中序数组
        for (int i = 0; i < inorder.length; i++) {
            //在中序数组中要找根节点所在位置
            if (inorder[i] == rootValue) {
         //以根节点为中心，将中序数组分为左部分和右部分，其中左部分即为根节点左子树的中序遍历数组
                int[] inLeft = Arrays.copyOfRange(inorder, 0, i);
                //右部分即为根节点右子树的中序遍历数组
                int[] inRight = Arrays.copyOfRange(inorder, i + 1, inorder.length);

               //通过中序遍历数组左右部分的个数，右可以将前序数组从第二个值开始分为左部分和右部分
                int[] preLeft = Arrays.copyOfRange(preorder, 1, i + 1);
                int[] preRight = Arrays.copyOfRange(preorder, i + 1, inorder.length);

                //分别把前序数组左部分和中序数组左部分，以及前序数组右部分和中序数组右部分看做一					颗数的前序遍历和中序遍历
                //递归调用buildTree方法返回根节点作为上一次返回根的左子树节点以及右子树节点
                root.left = buildTree(preLeft, inLeft);
                root.right = buildTree(preRight, inRight);

                // ** 切记！！ 在中序遍历数组中找到根的值后要跳出循环
                break;
            }
        }
        //返回根节点
        return root;
    }
}

这段代码定义了一个名为 Leetcode105 的类，它包含一个名为 buildTree 的方法，该方法接受两个整数数组 preorder 和 inorder 作为参数，并返回根据这两个数组构造出的二叉树的根节点。

buildTree 方法的主要逻辑如下：

1. 如果输入的数组为空，则返回空。
2. 取前序遍历数组的第一个元素作为根节点的值。
3. 遍历中序遍历数组，找到根节点所在位置。
4. 根据根节点的位置，将中序遍历数组分为左部分和右部分，其中左部分即为根节点左子树的中序遍历数组，右部分即为根节点右子树的中序遍历数组。
5. 根据左部分和中序遍历数组左部分的个数，将前序遍历数组从第二个元素开始分为左部分和右部分，其中左部分即为根节点左子树的前序遍历数组，右部分即为根节点右子树的前序遍历数组。
6. 分别递归地构造根节点的左子树和右子树，并将它们分别作为根节点的左子树节点和右子树节点。
7. 返回根节点。

在上述过程中，递归地调用 buildTree 方法，最终返回的根节点即为根据输入的前序遍历数组和中序遍历数组构造出的二叉树的根节点。

每日力扣：106. 从中序与后序遍历序列构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

?

输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

• 1 <= inorder.length <= 3000
• postorder.length == inorder.length
• -3000 <= inorder[i], postorder[i] <= 3000
• inorder 和 postorder 都由 不同 的值组成
• postorder 中每一个值都在 inorder 中
• inorder 保证是树的中序遍历
• postorder 保证是树的后序遍历

public class E10Leetcode106 {

    public TreeNode buildTree(int[] inorder, int[] postorder) {
      /*
        输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
            输出：[3,9,20,null,null,15,7]
        */
        //递归结束条件
        if(inorder.length==0){
            return null;
        }
        //后序遍历数组的最后一个值一定是根节点的值
        int rootValue = postorder[postorder.length-1];
        //有了根节点的值，创建根节点
        TreeNode root = new TreeNode(rootValue);
        //拿根节点在值，去中序遍历数组中找根节点的位置
        for (int i = 0; i < inorder.length; i++) {
            //在中序遍历数组中找到根节点位置
            if(inorder[i] == rootValue){

                //根据根节点位置划分数组
                int[] inLeft = Arrays.copyOfRange(inorder,0,i);
                int[] inRight = Arrays.copyOfRange(inorder,i+1,inorder.length);

                //划分后序遍历数组
                int[] postLeft = Arrays.copyOfRange(postorder,0,i);
                int[] postRight = Arrays.copyOfRange(postorder,i,postorder.length-1);

                //分别把后序数组左部分和中序数组左部分，以及后序数组右部分和中序数组右部分看做一				颗数的后序遍历和中序遍历
                //递归调用buildTree方法返回根节点作为上一次返回根的左子树节点以及右子树节点
                root.left = buildTree(inLeft,postLeft);
                root.right = buildTree(inRight,postRight);

                // ** 切记！！ 在中序遍历数组中找到根的值后要跳出循环
                break;
            }
        }
        return root;
    }
}

这段代码定义了一个名为 Leetcode106 的类，它包含一个名为 buildTree 的方法，该方法接受两个整数数组 inorder 和 postorder 作为参数，并返回根据这两个数组构造出的二叉树的根节点。

buildTree 方法的主要逻辑如下：

1. 如果输入的数组为空，则返回空。
2. 取后序遍历数组的最后一个元素作为根节点的值。
3. 遍历中序遍历数组，找到根节点所在位置。
4. 根据根节点的位置，将中序遍历数组分为左部分和右部分，其中左部分即为根节点左子树的中序遍历数组，右部分即为根节点右子树的中序遍历数组。
5. 根据左部分和中序遍历数组左部分的个数，将后序遍历数组从第一个元素开始分为左部分和右部分，其中左部分即为根节点左子树的后序遍历数组，右部分即为根节点右子树的后序遍历数组。
6. 分别递归地构造根节点的左子树和右子树，并将它们分别作为根节点的左子树节点和右子树节点。
7. 返回根节点。

在上述过程中，递归地调用 buildTree 方法，最终返回的根节点即为根据输入的中序遍历数组和后序遍历数组构造出的二叉树的根节点。