Leetcoder Day11｜栈与队列part03（队列的应用）

239.?滑动窗口最大值?

给定一个数组 nums，有一个大小为?k?的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的k个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值。

进阶：

你能在线性时间复杂度内解决此题吗？

示例 1：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

本题的难点在于，如何每次控制一个元素的进出以及在当前k个元素里寻找最大值。我们需要一个队列，在队列中放进去窗口里的元素，然后随着窗口的移动，队列也一进一出，每次移动之后，队列告诉我们里面的最大值是什么。因此需要自己设置一个这样的队列。

队列没有必要维护窗口里的所有元素，只需要维护有可能成为窗口里最大值的元素就可以了，同时保证队列里的元素数值是由大到小的。这个维护元素单调递减的队列就叫做单调队列，即单调递减或单调递增的队列。

那么如何取到窗口内最大元素呢？如果要push的元素大于队尾元素的值，那么就将队尾的元素弹出，直到push元素的值小于等于队列入口元素的值为止。这样就能保证队列的第一个元素即为最大元素。

如何移动窗口呢？若当前队列的第一个元素也就是最大值，为遍历到的当前元素，则pop队列中的这个元素，否则不用进行其他操作。

因此，单调队列的定义和构造如下：

class MyQueue{
     Deque<Integer> deque = new LinkedList<>();

     void push(int val){
         while(!deque.isEmpty() && val>deque.peekLast()){//当前元素值大于队尾值，则移除队尾元素
             deque.pollLast();
         }
         deque.offer(val);
     }

     void pop(int val){
         if(!deque.isEmpty() && val==deque.peek()){
             deque.pollFirst();
         }
     }

     int peek(){
         return deque.peekFirst();
     }
}

在定义单调队列的时候犯了一个很低级的错误，将int peek() 定义为了void，void返回的是方法，int返回数值，这里我们需要获取队首元素的值，因此应该是int。后面的代码如下：

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if(nums.length==1) return nums;
        int len=nums.length-k+1; //若原属数组是单调递增的，则最多能存放size-k+1个结果
        MyQueue queue= new MyQueue();
        int[] res = new int[len];       //存放结果元素的数组
        int count=0;//设置一个存放结果的计数器
        //先将前k的元素放入队列，实际上是一个只保存最大值及其后面比他小的值的单调递减序列
        for(int i=0;i<k;i++){
            queue.push(nums[i]);
        }
        res[count++]=queue.peek(); //将当前最大值存入
        //进行滑动
        for(int i=k;i<nums.length;i++){
            queue.pop(nums[i-k]);
            queue.push(nums[i]);
            res[count++]=queue.peek();
        }
        return res;
    }
}

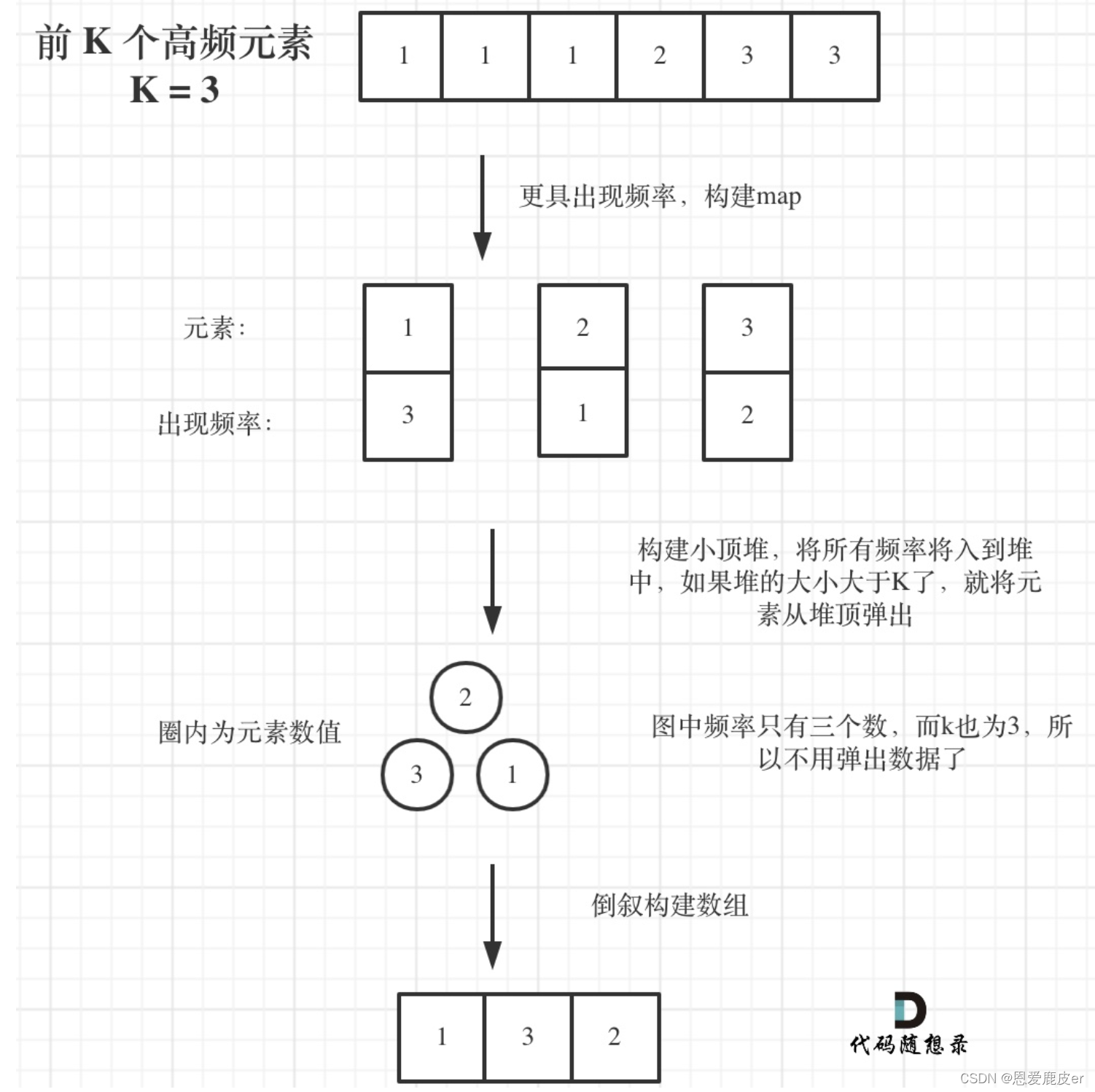
347.前?K?个高频元素

给定一个非空的整数数组，返回其中出现频率前 k 高的元素。

示例 1:

• 输入: nums = [1,1,1,2,2,3], k = 2
• 输出: [1,2]

示例 2:

• 输入: nums = [1], k = 1
• 输出: [1]

提示：

• 你可以假设给定的 k 总是合理的，且 1 ≤ k ≤ 数组中不相同的元素的个数。
• 你的算法的时间复杂度必须优于 O(n \log n)?, n 是数组的大小。
• 题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的。
• 你可以按任意顺序返回答案