HNU-数据挖掘-实验2-数据降维与可视化

发布时间：2024年01月22日

数据挖掘课程实验
实验2 数据降维与可视化

计科210X 甘晴void 202108010XXX
在这里插入图片描述

文章目录

数据挖掘课程实验<br>实验2 数据降维与可视化

实验背景

数据降维是指将高维数据映射到低维空间的过程。在现实生活中，很多数据集都是高维的，每个样本包含着大量特征。然而，高维数据不仅对计算资源要求较高，而且容易造成“维数灾难”，即在高维空间中，数据样本的稀疏性和分布规律难以理解。数据降维的目的是保留数据集的主要结构和信息，同时减少特征的维数，从而更好地进行数据分析和可视化。

实验目标

利用给定数据练习数据降维
熟悉基本的数据预处理方法
熟练掌握无监督数据降维方法
数据分布分析及可视化比较

实验数据集说明

数据集大小：(13627, 65)

行：基因。
列：第一列为基因名。

其余64列为数据。对应的列命名方式为：“A：B”。其中，A为数据来源，B为数据类别。这64列所有的列名如下：

‘MF: KIRC’, ‘MF: BRCA’, ‘MF: READ’, ‘MF: PRAD’, ‘MF: STAD’, ‘MF: HNSC’,

? ‘MF: LUAD’, ‘MF: THCA’, ‘MF: BLCA’, ‘MF: ESCA’, ‘MF: LIHC’, ‘MF: UCEC’,

? ‘MF: COAD’, ‘MF: LUSC’, ‘MF: CESC’, ‘MF: KIRP’, ‘METH: KIRC’,

? ‘METH: BRCA’, ‘METH: READ’, ‘METH: PRAD’, ‘METH: STAD’, ‘METH: HNSC’,

? ‘METH: LUAD’, ‘METH: THCA’, ‘METH: BLCA’, ‘METH: ESCA’, ‘METH: LIHC’,

? ‘METH: UCEC’, ‘METH: COAD’, ‘METH: LUSC’, ‘METH: CESC’, ‘METH: KIRP’,

? ‘GE: KIRC’, ‘GE: BRCA’, ‘GE: READ’, ‘GE: PRAD’, ‘GE: STAD’, ‘GE: HNSC’,

? ‘GE: LUAD’, ‘GE: THCA’, ‘GE: BLCA’, ‘GE: ESCA’, ‘GE: LIHC’, ‘GE: UCEC’,

? ‘GE: COAD’, ‘GE: LUSC’, ‘GE: CESC’, ‘GE: KIRP’, ‘CNA: KIRC’,

? ‘CNA: BRCA’, ‘CNA: READ’, ‘CNA: PRAD’, ‘CNA: STAD’, ‘CNA: HNSC’,

? ‘CNA: LUAD’, ‘CNA: THCA’, ‘CNA: BLCA’, ‘CNA: ESCA’, ‘CNA: LIHC’,

? ‘CNA: UCEC’, ‘CNA: COAD’, ‘CNA: LUSC’, ‘CNA: CESC’, ‘CNA: KIRP’

实验参考步骤

熟悉基本的数据预处理方法，对数据进行初步降维，降维到500-1000之内，降维方法可以自由选择。
熟练掌握无监督数据降维方法，比如PCA，ICA、UMap等
在不同的维度下面对数据进行数据分布分析及可视化比较。
实现数据的可视化，并进行适当的对比分析。

实验过程

在Linux平台下emogi环境中，进行数据降维与可视化。具体如下：

1.对数据进行初步降维

这里要注意结合题目要求，提供数据的列为样本，行为特征，这是一个与一般情况不同从而要小心的地方。但是一般我们把列作为数据特征，行作为数据样本。因此

使用方差阈值特征选择来进行降维，这样可以简单地剔除一些变化不大的数据。

方差阈值	结果维度
0.07	23
0.05	176
0.04	446
0.035	678
0.03	1039
0.01	6658

经过一些尝试，我发现方差阈值设定为0.035是比较好的，这样出来的结果维度为678维，处于要求的500-1000范围内。

这一部分的代码如下：

import pandas as pd
from sklearn.feature_selection import VarianceThreshold

# 读取数据集
data = pd.read_csv('实验二数据集.tsv', delimiter='\t', index_col=0)

# 转置数据以使样本在行上，特征在列上
data = data.T

# 1. 方差阈值特征选择
variance_threshold = VarianceThreshold(threshold=0.035)  # 调整阈值
data_variance_selected = variance_threshold.fit_transform(data)

# 获取选择的列索引
selected_columns = data.columns[variance_threshold.get_support()]

# 保存选择的列名到CSV文件，以逗号分隔
selected_columns_text = ','.join(selected_columns)
with open('selected_columns.csv', 'w') as file:
    file.write(selected_columns_text)

# 输出选择的列名
print("选择的列名：")
print(selected_columns)

# 输出降维后的维度
reduced_dimension = data_variance_selected.shape[1]
print(f"降维后的维度：{reduced_dimension}")

# 保存特征选择后的数据
selected_data = pd.DataFrame(data_variance_selected, columns=selected_columns)
selected_data.to_csv('selected_data.csv', index=False)

筛选结果如下（以下为678个）：

EGFR,PIK3CA,PTEN,TP53,SCO2,BIRC5,SFN,TPX2,POU4F2,RUNX1,CTSK,SERPINB13,SMAD4,TNFRSF10D,GRIA2,TFB2M,SBF1,HRG,NLRP3,GLP2R,FSHB,GLI2,KCNJ16,TAC1,NCAM1,CD300E,CD300LB,GRAP2,IL18,KNG1,S100A8,ID1,CASP8,MYC,SIRPG,PTK6,JAM3,ANGPT2,GAD2,HTR3C,MASP1,CSF2,ITGA8,CIDEC,C6,PAX3,APC,CDKN2A,SETDB1,PGLYRP4,PGLYRP3,ANK1,CHL1,ROBO2,CFTR,CD1B,CD1C,SDHA,ARNT,PITX2,NRG1,TNFRSF10C,DOK2,DOCK2,SLC6A3,IL1A,WT1,FLT4,EXOC3,MYOCD,MUC20,IRF4,BCL2L1,NRG3,NFATC1,CNGB3,MAPK12,TERT,NR0B2,MCL1,RB1,SKIL,LEP,ITK,FCRL3,GHSR,DAPP1,MAP2K4,NSD1,CRP,MAGEA1,KRT17,PRKCI,HOXA9,SOX1,CLIP3,LILRA4,APCS,MAPK11,LNX1,INA,ZBTB16,ACTN2,FCN1,GPRASP1,KRT16,SERPINB5,SERPINB3,MYH1,CCL14,ACTA1,CARD6,SDCCAG8,RUSC1,SPARC,AKT3,LTC4S,MUC16,ALX1,ARHGAP32,KRT6B,LILRB4,SPRR2A,KRT15,MAP1LC3A,OTX2,LGALS8,OLIG3,HNRNPU,MYLK2,DRD4,ADAMTSL1,ESRRG,PARD6G,NID2,S100A12,AJAP1,CCL8,H2AFY,RGS7,SERPINB12,MAPK8IP2,SOX11,SPERT,ANXA9,TCP10,MMP13,PHF19,VHL,MAP1LC3C,SHANK3,SKOR2,FCER1A,AHCTF1,KHDRBS2,KCNA4,DCD,DUSP15,PITX1,HOXC6,AIM2,PTGDR,DPP6,SOX17,PPP6R2,TCEAL2,VIPR2,DES,CRELD2,ADSS,SPRR2G,ZFP42,TAGLN,IRX1,CEP72,GNG4,ADH1B,SCTR,ALDOB,TRIP13,HAVCR2,KRT6A,SPRR1A,TK1,KRTAP11-1,KRTAP6-2,TBX15,APOBEC1,CCL11,USP6,TBX18,SUB1,SERTM1,SCGB3A1,SLC7A14,SLC32A1,GCM2,PCDHGA9,FAT1,VAX1,KRTAP8-1,GGT6,PDCD6,MKRN3,ZNF835,KRTAP13-3,SLC30A8,REG1B,NPM2,KRTAP26-1,GRXCR1,CRMP1,NCAPH2,TTN,TMCO5A,ASPA,KPRP,PAX7,GYPC,PLP1,BOLL,TMPRSS4,MEOX2,CRYAB,PRDM14,CDX2,AQP2,LAMP3,LCE4A,LCE2B,PQLC1,RYR2,ZSCAN12,GSTM5,LCE1A,LCE1B,FOXI1,ZNF496,FERD3L,LCE1D,SOX2,ZNF124,HRH1,DLC1,TLX3,AGR2,ZIC1,CA4,DNASE1L3,KCNA1,CLDN11,KRTAP19-1,FH,SLC26A3,SNTB1,ACTC1,DNAH8,NXPE2,ZNF670,UGT1A6,LIME1,SOX10,SLC9A3,ARSA,CERS2,PLN,CACNG7,KCNA6,BARHL2,C11orf87,LAYN,MYH11,TRH,KCNIP4,COX20,CLVS2,FHL5,KRT5,PTPRN,CTXN3,ZBTB18,KRT4,CNTN4,HBG2,HAND2,SYT6,SPRR3,RPRD2,GAS7,CEP170,FRG1,CLDN8,MAGI2,ECM1,NEFM,AICDA,TM4SF19,SPP1,SYCE3,LCE1C,ADRA1A,LCE2D,LAIR2,SSTR2,PDRG1,LCE2A,SPARCL1,GREM1,SLC12A7,TBX5,BRD1,SLC35F1,APOH,ADCYAP1,HM13,SFTPC,KRT80,NRIP2,CMTM2,C14orf180,TRIM29,KRTAP23-1,EPHA7,PEBP4,KRTAP7-1,RBFA,SOX3,CA3,SPDYA,ZSCAN23,PPP1R16B,TPPP,NKX2-6,FUT9,PAX9,VWC2,HOXD12,RXFP3,HIST1H4F,MLC1,SEC62,HDAC10,MYNN,NKD2,TRDN,SMYD3,FCRL4,HTR1B,APOA4,SCG5,HTR1A,ZNF626,ACOT12,QRFPR,RHOBTB2,CD300LG,ZNF135,PLXNB2,GDNF,ZNF692,ZBED4,DNTT,FAM107A,KCNA3,ZDHHC11,RIPPLY2,SCARA5,SPANXD,REC8,TMC6,CKMT2,ZNF334,LPAR6,RHCG,HRNR,NEUROD6,SLC13A5,CNST,CTDP1,NPBWR1,FGD5,EVX2,TXNL4A,EXO1,TMX3,GC,LGI3,IFNL1,ENSA,CCDC105,PI16,FRG2,ADHFE1,CASQ2,PENK,LCE3D,GJA10,MSC,RAB25,DPPA2,CARTPT,AVPR1A,BPIFA1,UBD,FAM83D,MBP,ADAMTS12,AQP8,ZNF695,LOXL2,ZNF669,BARX1,HOXD9,GABPB2,EYA4,NFIA,CNTNAP2,MYH8,SIX3,GRIA4,CA9,PTPRD,MFAP4,SPOCK1,FCRL2,POU3F3,HSPB6,PABPC5,LMF2,BLID,LYPD5,CA1,MYH13,MYOC,NOVA1,KCNN2,GP2,SNAP91,GOLPH3L,ANGPTL7,COX4I2,ADAM28,SYCP1,DEFB121,HORMAD2,TCF24,PEX5L,ACTG2,SPATA16,C1orf116,SPHKAP,COL10A1,CDO1,ASCC1,TGIF2LX,ZFP28,GLYAT,SEMG1,FGF10,IFFO1,KCNAB3,ZNF804B,IRX4,ZSCAN1,ZIK1,LEFTY2,KIF26B,EID3,CDC42SE1,PIK3R6,PIWIL2,CPB2,SLITRK5,NPY,SALL1,CCDC181,TMPRSS11F,GATA5,CRNN,ST8SIA5,KIF2B,IVL,CCL15,CHRM2,SLC18A3,HOXD10,FOXG1,OLIG2,SLAMF7,PCSK1,TCHH,PIM3,CTNNA2,KRTAP13-4,ZNF292,UTF1,GRIK5,CDH4,ZNF671,NR2E1,GPR87,FOXS1,CLCA4,C1orf56,CCR6,GFRA1,SETMAR,PCDHA7,IFNA8,SUMF1,SLC27A6,SYT9,PRSS1,F11,CMA1,CDH7,DPT,GRIN3A,SCN2B,CHRNA2,NID1,SLCO1A2,CST7,REG1A,REG3A,CSTA,GABRB2,GABRG3,SYN2,KCNJ1,DRD5,REM1,BNIPL,CTSS,HOXB4,CD5L,CHML,SCN10A,ADCY8,PHOX2A,GSTM1,CDH19,AHRR,GRIK2,PI3,HAVCR1,PGM5,C7,CBLN1,CP,FCAR,GABRB3,SPAG6,LAMB3,CST5,ZP4,GALNT13,GRM7,GRM6,MYH4,PCDHA6,GRP,BCHE,PTF1A,GPR26,KCNQ5,KCNK9,SLC5A7,RAX,BST1,CHRDL1,SIX6,PAX1,GREM2,CD300LF,TPO,ZNF382,DLK1,CHAD,CBLN4,KCNG2,ACR,SIM1,EDN3,CD1E,TYR,TBX20,ZC3H12D,HBG1,PYHIN1,ZNF516,C10orf90,PCDHGA11,TARS2,GFRA2,SALL3,FBLL1,GPR142,TYMP,TUBGCP6,BHMT2,DIO3,ZNF454,ZNF625,ZFP82,ZNF716,OR7G3,CHKB,PLA2G4F,ALG12,AGXT2,ST6GALNAC1,TRIM71,FEZF2,KRTAP13-1,ZNF471,HORMAD1,HTR1E,NXPH2,GPM6A,MAP1LC3B2,OGN,VSIG2,EMILIN3,ST6GALNAC5,SERPINB7,OR51E2,SCCPDH,SERPINB11,S100A7A,ZACN,LIPH,DNAI2,FABP7,RTL1,TBX4,SLCO4C1,ZSCAN5A,PCDHB15,FOXE1,FOXI2,NELL1,ZIC5,NKX1-1,OR2W3,PCDHA12,PCDHA3,PCDHGB5,PCDHGB4,PCDHGA5,PCDHGB3,PCDHGC4,CST1,PCDHGA7,HS3ST2,GABRA6,SLC39A12,ZNF732,RFTN2,SPATA19,PCDHGA12,MICU3,LRRN1,SIRPD,TTLL9,DEFB104B,SLCO1B1,KMO,ZNF672,BPIFB1,TMEM40,SORCS1,SPRR1B,KIF19,OR51B6,CSH1,ADIG,CSMD1

2.使用无监督数据降维方法，比如PCA，ICA、UMap等进行降维

在刚刚筛选出结果特征的基础上进行进一步降维，这一步使用无监督数据降维方法。

（1）主成分分析（PCA）降维

使用主成分分析（Principal Component Analysis，PCA）进行降维。

①基础知识

协方差矩阵：首先，PCA计算数据的协方差矩阵，该矩阵描述了数据中各特征之间的相关性。协方差矩阵的对角线元素是每个特征的方差，非对角线元素表示不同特征之间的协方差。
特征值分解：PCA通过对协方差矩阵进行特征值分解，得到特征值和特征向量。特征向量是与协方差矩阵特征值对应的向量，它们描述了数据中的主要方向。
选择主成分：特征向量按照对应特征值的大小排序，选择前k个特征向量作为主成分，其中k通常小于或等于原始数据的维度。这些主成分代表了数据中的主要变化方向。
投影：将原始数据投影到所选的主成分上，得到新的数据集。这个过程将数据从高维空间投影到低维空间，从而减少了维度。
重建：如果需要，可以使用投影后的数据和所选的主成分来重建原始数据，虽然这不是PCA的主要目标，但在某些应用中可能有用。

②评价指标

使用累计方差解释比例（Cumulative Variance Explained）刻画PCA降维结果维度方差对于总方差的贡献，也就是降维结果的主成分包含原数据信息的程度。

下面解释这个概念。

方差解释比例（Variance Explained Ratio）：每个主成分都能够解释原始数据中的一定比例方差。这个比例通常以百分比表示，例如，第一个主成分可能能够解释数据总方差的30%，第二个主成分能够解释15%，以此类推。
累计方差解释比例（Cumulative Variance Explained Ratio）：累计方差解释比例是指前n个主成分（或因子）的方差解释比例之和。它告诉我们，在保留了这些主成分的情况下，原始数据中的总方差的多少被解释了。通常，我们希望保留足够多的主成分，以使累积方差解释比例达到某个预定的阈值，以确保保留了足够的信息，同时降低数据维度。
选择主成分数量：根据累积方差解释比例，可以决定保留多少主成分。一般来说，当累积方差解释比例达到一个满意的水平（通常在70%到95%之间）时，可以考虑停止增加主成分的数量，因为这足够解释大部分数据的方差。

下面是指定不同降维维度后该参数的结果。

目标维度（n_components）	累计方差解释比例（Cumulative Variance Explained）
64	100%(未开始降维)
50	99.63%
40	97.94%
30	94.11%
20	87.13%
15	82.25%
14	81.12%
13	79.88%
10	75.32%
5	62.69%
1	36.66%

一般来说，累计方差解释比例低于50%是不可信的。在50%到80%时一般可信。在80%以上则称为可信。

按照这种观点来看，我们可以选择14维作为目标维度，使用PCA进行降维，并利用降维的结果绘制部分主成分之间的三点关系图。

这里我们考虑到数据的“数据来源”与“数据类别”两个标签，其中“数据类别”有16种，不太适合分组呈现，故我这里就“数据来源”的不同取值“MF”，“METH”，“GE”，“CNA”进行分组分颜色显示。

③可视化

首先获取最大的两个主成分PC1和PC2的散点关系图，可以发现MF的聚类情况表现地较明显，即MF来源的数据相似情况较大。

在这里插入图片描述

接下来查看前5个PCA主成分之间的相互散点关系图

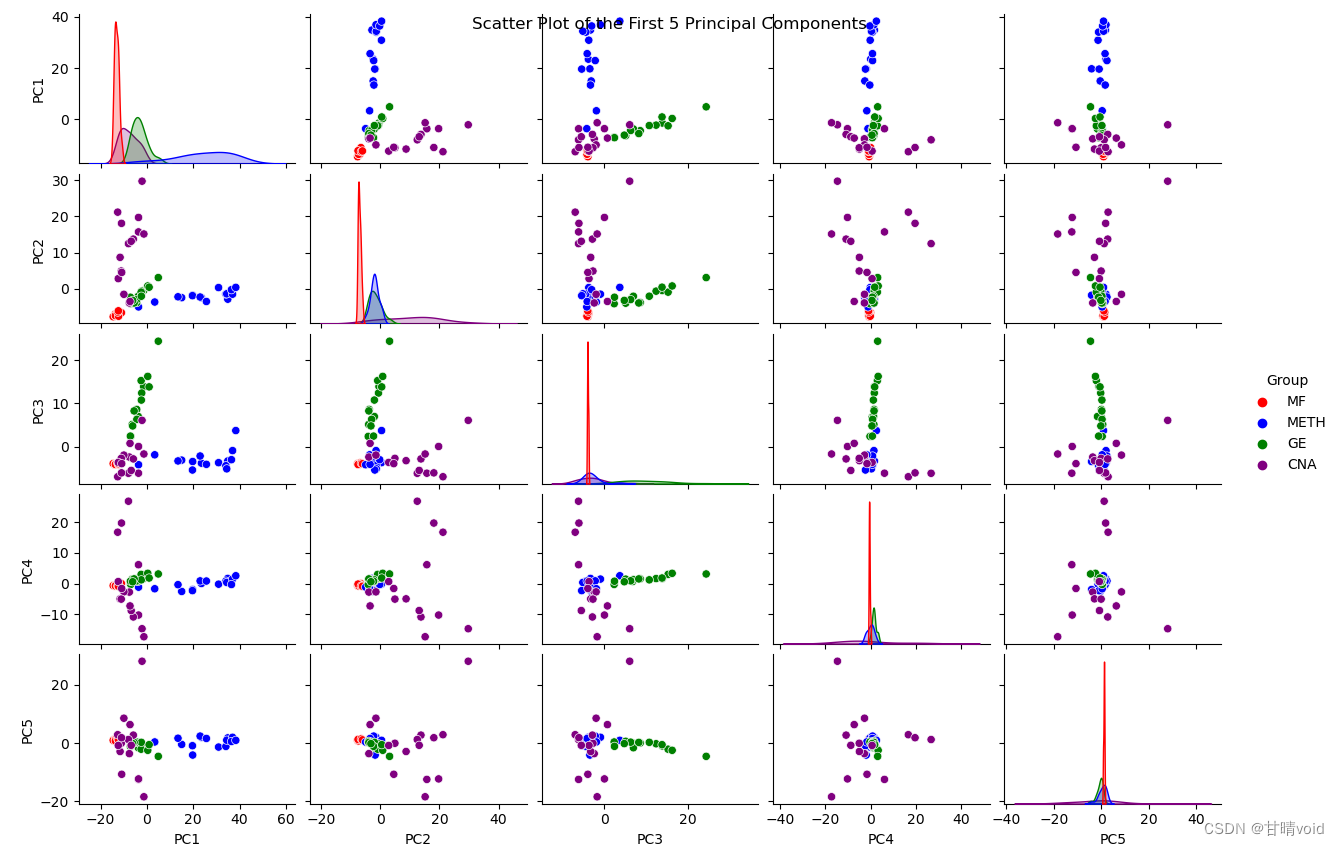
在这里插入图片描述

可以发现，仅使用PC1与PC2主成分已经能够较为完美地完成相似数据的分类任务。

进一步，我们可以在三维图视下查看前三个主成分的互相关系。

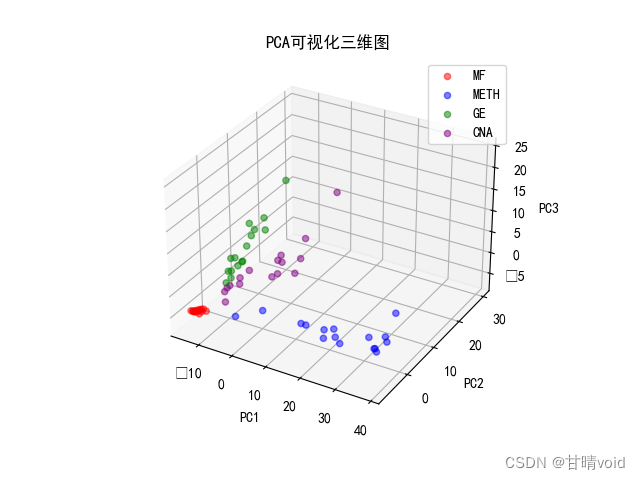
在这里插入图片描述

★问题探究：改变n_components，PCA主成分并没有变化？

这里具体执行会遇到一个小问题，即n_components，看上去PC的值并没有改变。实际上这里是因为变化过于微小导致看上去并没有变化，如果我们将小数位数放多一些，实际上还是有明显的变化的。

Explained Variance Ratio for PC1: 36.66%
Explained Variance Ratio for PC2: 9.68%
Explained Variance Ratio for PC3: 6.56%
Explained Variance Ratio for PC4: 5.64%
Explained Variance Ratio for PC5: 4.14%
Explained Variance Ratio for PC6: 3.35%
Explained Variance Ratio for PC7: 2.84%
Explained Variance Ratio for PC8: 2.49%
Explained Variance Ratio for PC9: 2.05%
Explained Variance Ratio for PC10: 1.90%
Explained Variance Ratio for PC11: 1.68%
Explained Variance Ratio for PC12: 1.51%
Explained Variance Ratio for PC13: 1.37%
Explained Variance Ratio for PC14: 1.24%
Cumulative Variance Explained by 14 Principal Components: 81.12%

我们将小数位数放到10位。

n_components = 5

Explained Variance Ratio for PC1: 36.6633189992%
Explained Variance Ratio for PC2: 9.6806797212%
Explained Variance Ratio for PC3: 6.5627968456%
Explained Variance Ratio for PC4: 5.6423145826%
Explained Variance Ratio for PC5: 4.1373794292%
Cumulative Variance Explained by 5 Principal Components: 62.69%

n_components = 14

Explained Variance Ratio for PC1: 36.6633189992%
Explained Variance Ratio for PC2: 9.6806797201%
Explained Variance Ratio for PC3: 6.5627968242%
Explained Variance Ratio for PC4: 5.6423145516%
Explained Variance Ratio for PC5: 4.1373791936%
Explained Variance Ratio for PC6: 3.3504752123%
Explained Variance Ratio for PC7: 2.8403813497%
Explained Variance Ratio for PC8: 2.4943752057%
Explained Variance Ratio for PC9: 2.0477662556%
Explained Variance Ratio for PC10: 1.9012579517%
Explained Variance Ratio for PC11: 1.6803878986%
Explained Variance Ratio for PC12: 1.5090011367%
Explained Variance Ratio for PC13: 1.3680188469%
Explained Variance Ratio for PC14: 1.2435843400%
Cumulative Variance Explained by 14 Principal Components: 81.12%

可见数据还是改变了。

原因可能在于数据中的特征之间没有足够的差异，或者特征之间的相关性非常高，导致 PCA 的主成分没有多大变化，初步判定应该是数据本身的问题，主成分的方法没有太大的问题。

（2）独立成分分析（ICA）降维

使用独立成分分析（Independent Component Analysis，ICA）进行降维。

①基础知识

数据收集：首先，收集需要进行ICA处理的混合信号数据集。这些混合信号可以是音频、图像、生物信号（如脑电图或心电图）、金融时间序列等。
数据预处理：在开始ICA之前，通常需要对数据进行一些预处理，以确保信号的均值为零，并可能对数据进行缩放，以便处理过程更有效。这通常包括中心化和标准化。
建立混合模型：定义混合模型，假设混合信号是独立成分的线性组合。这个模型通常表示为X = AS，其中：
- X 是观测到的混合信号矩阵，每一列代表一个观测时间点或传感器通道。
- A 是混合矩阵，包含了混合系数，表示混合成分与观测信号之间的关系。
- S 是独立成分矩阵，包含了独立成分的时间序列或通道。
ICA估计：在这一步，估计混合矩阵 A 和独立成分矩阵 S。这通常涉及到最大独立性估计（maximum likelihood estimation for independent sources, maximum entropy ICA）等方法。ICA算法的目标是找到A和S，使得S中的各行（独立成分）是统计上不相关的。
成分排序和解释：ICA通常无法确定成分的顺序，所以需要进一步的分析来解释这些成分。这包括对成分的统计性质的研究，如成分的概率密度函数、峰度和偏度等。此外，领域专业知识也有助于解释和排序成分。
可视化和应用：最后，得到的独立成分可以用于各种应用，如信号分离、特征提取、数据降维、噪音过滤等。可视化工具和技术可以帮助理解和验证ICA的结果。

②评价指标

在独立成分分析（ICA）模型中，信噪比（SNR，Signal-to-Noise Ratio）和互信息（MI，Mutual Information）是两种评价指标，用于评估ICA分离的成分的质量。这些指标有助于确定分离的成分是否保留了原始信号的相关信息，同时也可以用于比较不同ICA模型的性能。

SNR（信噪比）：

定义：SNR用于衡量ICA分离的信号成分与噪声之间的相对强度。在ICA的背景下，这意味着SNR用于度量独立成分的清晰度，即成分中信号与噪声的比例。
计算方式：SNR的计算通常涉及以下步骤：
1. 选择一个ICA分离的成分。
2. 计算该成分的功率或能量。
3. 计算该成分中的噪声的功率或能量。
4. 使用下述公式计算SNR：SNR(dB) = 10 * log10(信号功率 / 噪声功率)
应用：SNR可用于衡量每个ICA成分中信号和噪声的相对强度。更高的SNR表示信号更容易识别，而更低的SNR可能意味着成分中有更多的噪声干扰。

MI（互信息）：

定义：互信息是一种度量，用于衡量ICA分离的成分与原始信号之间的信息传输量。它可以帮助确定分离的成分是否包含原始信号的信息。
计算方式：计算互信息通常需要以下步骤：
1. 计算原始信号与ICA成分之间的联合分布。
2. 计算原始信号的边缘分布和ICA成分的边缘分布。
3. 使用这些分布计算互信息，通常使用互信息的定义：MI(X, Y) = ∫∫ p(x, y) * log(p(x, y) / (p(x) * p(y))) dx dy，其中 X 表示原始信号，Y 表示ICA成分。
应用：互信息可用于衡量ICA成分与原始信号之间的相关性。较高的互信息表示成分保留了更多原始信号的信息。

峰度（Kurtosis）：

定义：峰度是用于描述概率分布尾部（尤其是高阶短尾或长尾）相对于正态分布的“尖锐度”或“平缓度”的统计量。它用于度量分布中数据点分布的尖峰程度。
计算方式：峰度通常计算为数据集中数据点的四次方的期望值与方差的四次方之比。具体计算方式取决于不同的定义，其中一种常见的方式是使用以下公式：Kurt(X) = E[(X - μ)^4] / (σ^4)，其中 X 是数据集，μ 是均值，σ 是标准差。
应用：在ICA中，峰度可以用于评价分离的成分是否服从非高斯分布。高峰度值可能表示成分具有尖峰或重尾，这与高斯分布不同。

偏度（Skewness）：

定义：偏度用于描述数据分布的不对称性，即数据在分布中的偏向。正偏度表示数据右偏，负偏度表示数据左偏，零偏度表示分布对称。
计算方式：偏度通常计算为数据集中数据点与均值的三次方的期望值与方差的三次方之比。常见的计算方式是：Skew(X) = E[(X - μ)^3] / (σ^3)，其中 X 是数据集，μ 是均值，σ 是标准差。
应用：在ICA中，偏度可以用于检测成分是否具有非对称性，即是否存在明显的左偏或右偏特征。非对称性可能表明成分不是高斯分布。

这里我们可以尝试不同的目标降维维度并获取它们的SNR、MI、峰度和偏度值来判断ICA模型的好坏。

简单来说，相同情况下，SNR与MI较大会更好一些，峰度和偏度也是较大会更好一些。

③维度选择与可视化

尝试改变n_components 并探究这四个参数的变化。

当n_components =3时，相关参数如下

Signal-to-Noise Ratio (SNR): 53.28
Mutual Information (MI) with True Signal: 3.6379
  Component  Kurtosis  Skewness
0       IC1  1.811055 -1.561985
1       IC2  0.604004  0.946129
2       IC3 -1.067555  0.467046

在IC1与IC2方向上所得散点图如下

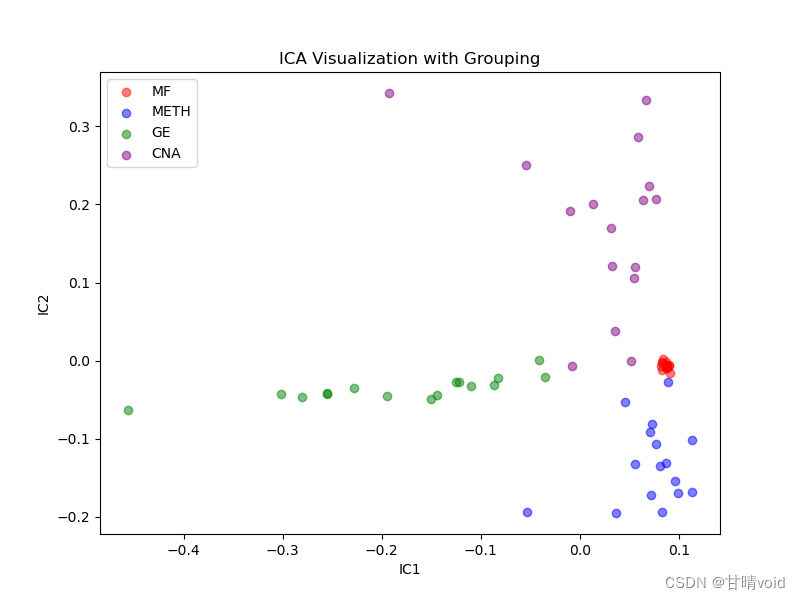
在这里插入图片描述

由于这里只有三个IC值，IC1,IC2,IC3三个，挑选它们并以这三个独立成分为轴绘制三维图如下

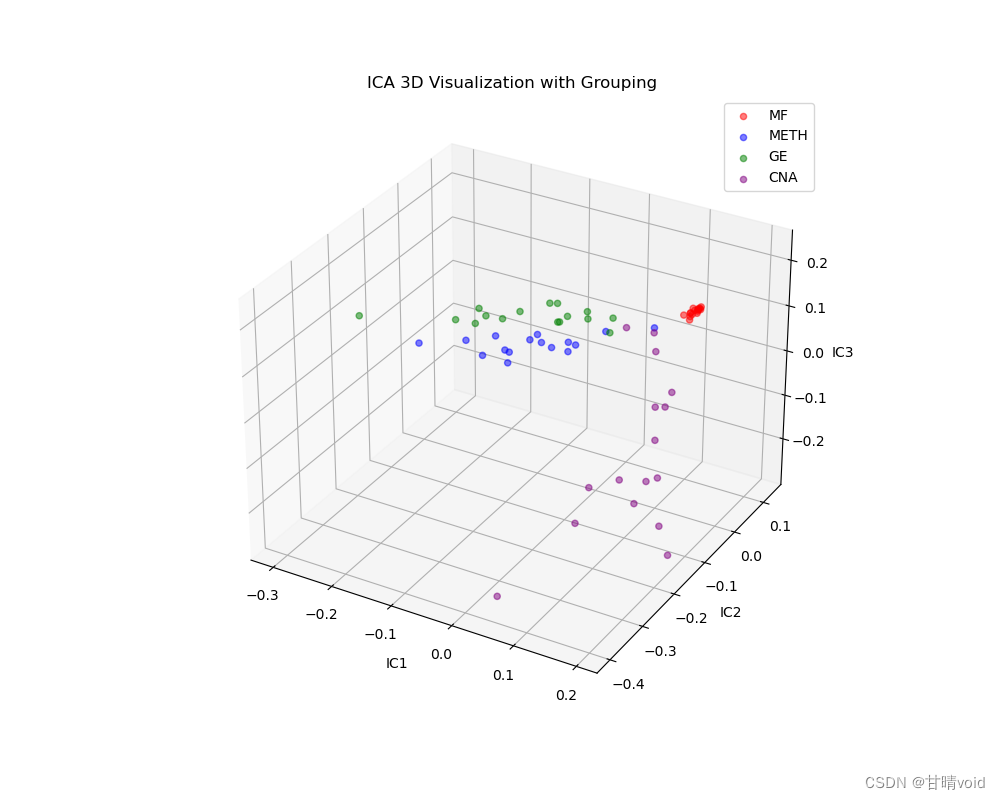
在这里插入图片描述

当n_components =10时，相关参数如下

Signal-to-Noise Ratio (SNR): 2.57
Mutual Information (MI) with True Signal: 3.6379
  Component   Kurtosis  Skewness
0       IC1  -0.798939 -0.287743
1       IC2   0.744784 -0.457725
2       IC3   5.696764  2.139519
3       IC4  20.054037 -3.384852
4       IC5  40.362070 -6.036482
5       IC6  41.987941  6.188286
6       IC7  20.493603 -4.103255
7       IC8  26.287692 -4.377644
8       IC9  14.829184 -3.959355
9      IC10  15.423052  3.054299

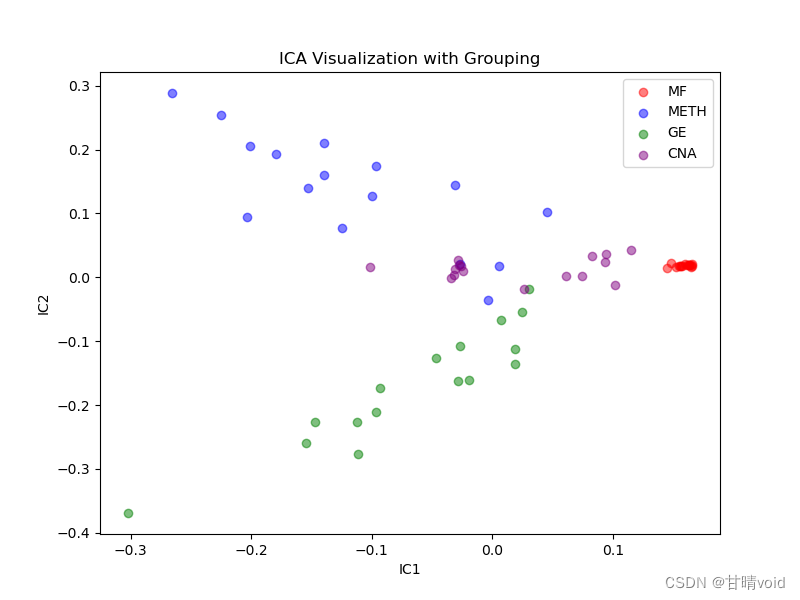
在这里插入图片描述

挑选峰值较大的三个IC值，IC4,IC5,IC7三个，并以这三个独立成分为轴绘制三维图如下

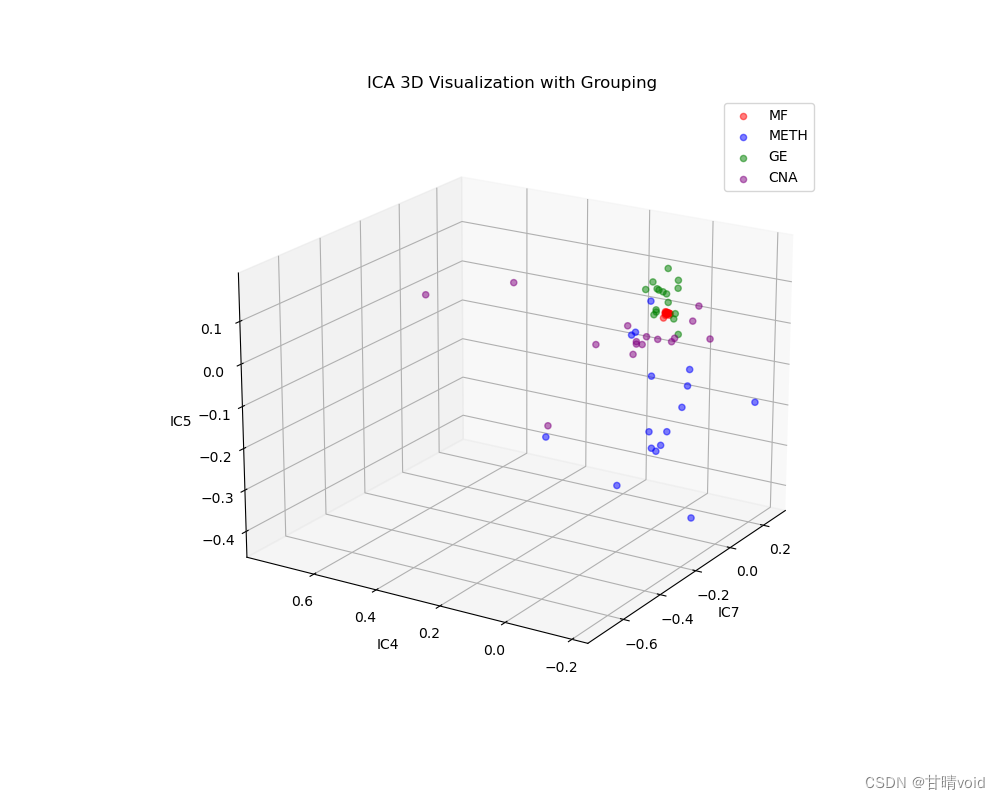
在这里插入图片描述

可以发现效果还是不错的。

（3）Umap降维

①基础知识

UMAP（Uniform Manifold Approximation and Projection）是一种非线性降维技术，用于将高维数据映射到低维空间以进行数据可视化、聚类和降维分析。UMAP是一种基于流形学习的方法，旨在保留数据中的局部结构和全局结构，并在降维后尽量保持数据点之间的拓扑关系。

主要步骤如下：

高维数据表示：UMAP从高维数据集开始，通常以N×D的形式表示，其中N是样本数量，D是特征维度。
构建连通图：UMAP首先构建一个表示数据点之间连接的权重图。这一步骤包括以下子步骤：
- 确定邻近性：对于每个数据点，UMAP确定其在高维空间中的k个最近邻居。这是通过计算数据点之间的距离来完成的。
- 权重计算：UMAP计算每对邻近数据点之间的权重，反映它们之间的连接强度。UMAP使用距离度量来计算权重，通常采用高斯核函数来赋予邻近点更高的权重，而远离点较低的权重。
优化连通图：UMAP使用拓扑优化技术，如随机梯度下降，来最小化在低维空间的连通图与高维连通图之间的拓扑误差。这有助于保留数据的全局结构。
低维嵌入：UMAP将优化后的高维连通图映射到低维空间。通常，UMAP将数据映射到2D或3D空间以进行可视化。映射是通过优化低维坐标以最小化高维图与低维图之间的拓扑误差来实现的。

②重要参数

UMAP两个重要的参数

n_neighbors：最重要的参数是n_neighbors，用于构造初始高维图的近似最近邻的数量。它有效地控制UMAP如何平衡局部结构与全局结构：较小的值将通过限制在分析高维数据时考虑的相邻点的数量来推动UMAP更多地关注局部结构，而较大的值将推动UMAP代表全局结构，同时失去了细节。
min_dist：第二个参数是 min_dist，即低维空间中点之间的最小距离。此参数控制UMAP将点聚集在一起的紧密程度，较低的值会导致嵌入更紧密。较大的 min_dist值将使UMAP将点更松散地打包在一起，而是专注于保留广泛的拓扑结构。

③可视化

使用umap的二维可视化

在这里插入图片描述

使用umap的三维可视化

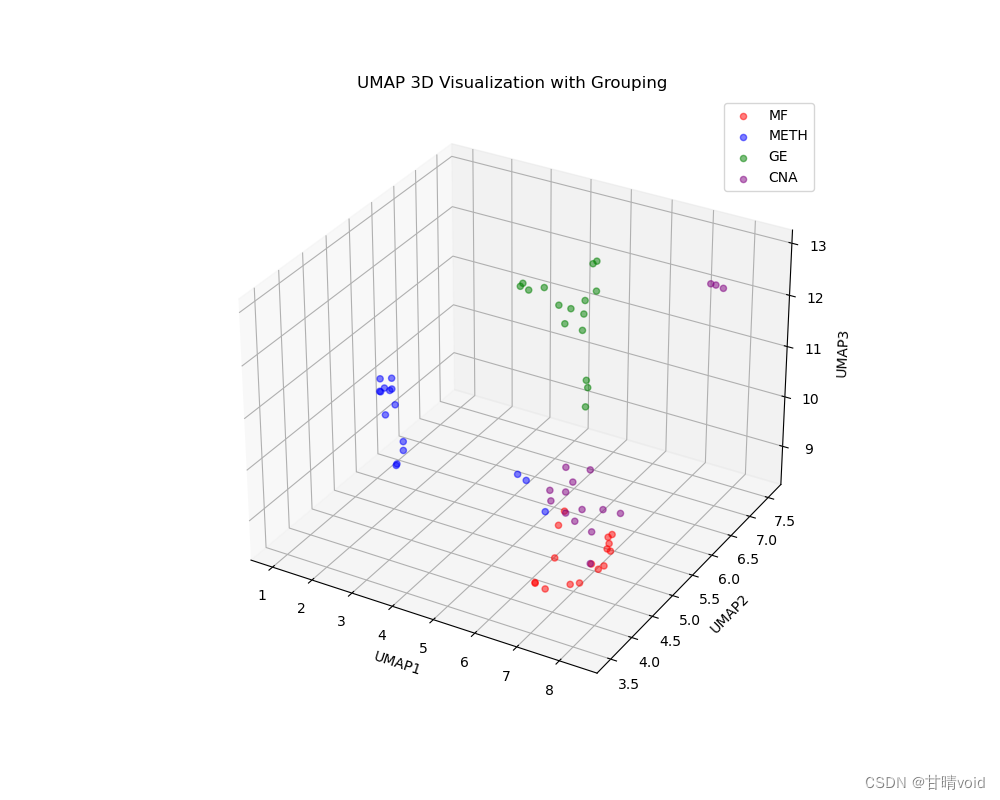
在这里插入图片描述

可以看到，基本能够完成对于数据的降维与分步分析的功能。

3.使用t-SNE进行可视化

①基础知识

t-SNE（t-Distributed Stochastic Neighbor Embedding）是一种非线性降维技术，用于将高维数据映射到低维空间，以便进行可视化和数据分析。它是一种流形学习方法，旨在保持数据点之间的相似性关系，特别是在局部结构上。t-SNE的核心思想是将高维数据点映射到低维空间，以便在低维空间中更好地表示相似性关系。

主要特点：

非线性映射：t-SNE采用非线性映射，因此能够捕获数据中的复杂结构和非线性关系。
局部保持：t-SNE着重于保持数据点之间的局部相似性关系，这使得它在可视化和聚类分析中特别有用。
概率建模：t-SNE使用概率分布来建模数据点之间的相似性，其中高维和低维空间中的点之间的相似性关系通过概率分布来表示。
参数设置：t-SNE有一些参数，包括困惑度（perplexity）和学习率（learning rate），可以用来控制嵌入的特性。

计算过程：

相似性矩阵：首先，计算高维数据点之间的相似性矩阵，通常使用高斯核函数计算数据点之间的条件概率分布。这个相似性矩阵表示了每对数据点之间的相似性。
低维概率分布：t-SNE使用概率分布来表示数据点在低维空间中的位置。这个分布是在低维空间中为每个数据点定义的。
目标函数：t-SNE通过优化一个目标函数来确定低维空间中的数据点位置，使得高维和低维空间中的相似性分布尽可能匹配。这个目标函数通常是一个KL散度，用来测量高维和低维概率分布之间的差异。
梯度下降：通过梯度下降等优化技术，调整低维空间中的数据点位置，以最小化KL散度。

t-SNE的优点包括在可视化中捕获局部结构，适用于高维数据和非线性关系的数据集。然而，t-SNE也有一些挑战，如困惑度的选择对结果的影响，以及计算复杂性的增加。在实践中，通常需要不同的参数设置和实验来获取最佳的嵌入结果。

②可视化

在第一步PCA降维到14维的基础上进一步进行降维，读取PCA的14维结果进行进一步降维，最终降到2或3维。

选定超参数random_state=7，实际上这是一个随机化的过程，指定超参数可以增强可重复性，相当于规定了这个条件。

二维可视化

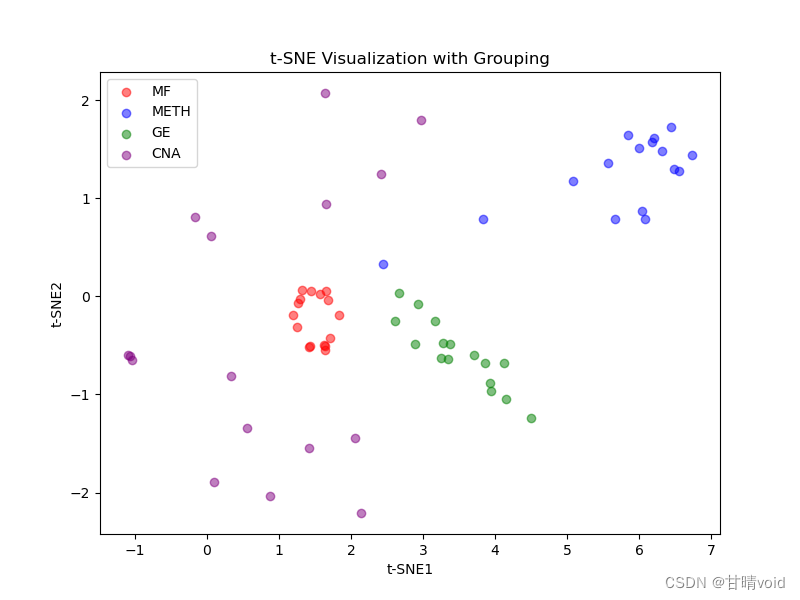
在这里插入图片描述

三维可视化

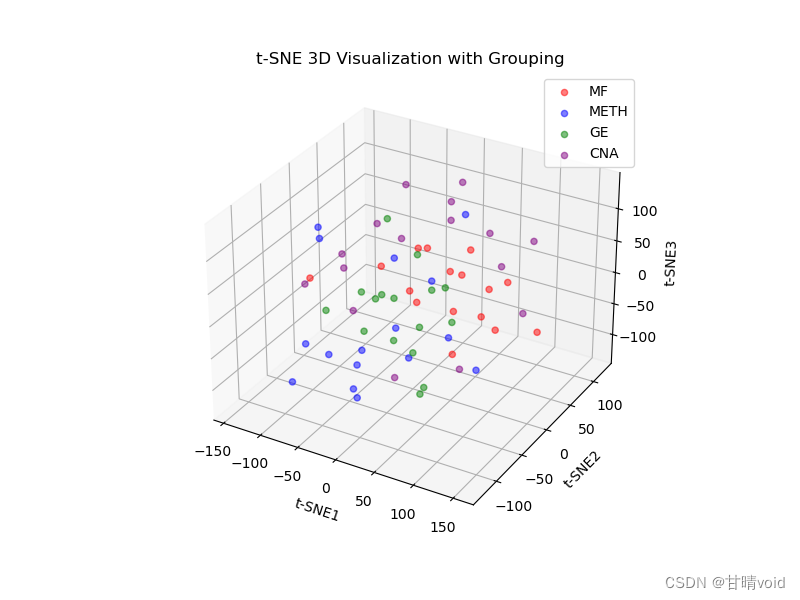
在这里插入图片描述

附录：中间过程csv文件的解释

pca_processed.csv（经过PCA降维后的数据，用于t-SNE处理）
selected_columns.csv（经过特征选择降维之后的数据特征名）
selected_data.csv（经过特征选择降维之后的数据）

附录：代码

1、特征选择降维（预处理）代码

import pandas as pd
from sklearn.feature_selection import VarianceThreshold

# 读取数据集
data = pd.read_csv('实验二数据集.tsv', delimiter='\t', index_col=0)

# 转置数据以使样本在行上，特征在列上
data = data.T

# 1. 方差阈值特征选择
variance_threshold = VarianceThreshold(threshold=0.035)  # 调整阈值
data_variance_selected = variance_threshold.fit_transform(data)

# 获取选择的列索引
selected_columns = data.columns[variance_threshold.get_support()]

# 保存选择的列名到CSV文件，以逗号分隔
selected_columns_text = ','.join(selected_columns)
with open('selected_columns.csv', 'w') as file:
    file.write(selected_columns_text)

# 输出选择的列名
print("选择的列名：")
print(selected_columns)

# 输出降维后的维度
reduced_dimension = data_variance_selected.shape[1]
print(f"降维后的维度：{reduced_dimension}")

# 保存特征选择后的数据
selected_data = pd.DataFrame(data_variance_selected, columns=selected_columns)
selected_data.to_csv('selected_data.csv', index=False)

2、PCA基础代码

import pandas as pd
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import seaborn as sns

# 读取CSV文件，header=None表示没有列标签
data = pd.read_csv('selected_data.csv', header=0)

# 提取特征（所有列）
features = data.iloc[:, :]

# 对特征进行标准化
scaler = StandardScaler()
scaled_features = scaler.fit_transform(features)

# 指定降维后的维度
n_components = 14  # 降维后的维度

# 创建PCA模型并进行降维
# 若n_samples >= n_features,则可以调用最大似然估计法自动选择超参数
# pca = PCA(n_components="mle")
# pca_f = PCA(n_components=0.97, svd_solver="full")可以按信息量占比自动选择超参数
pca = PCA(n_components=n_components)
pca_result = pca.fit_transform(scaled_features)

# 将降维后的结果转换为DataFrame
pca_df = pd.DataFrame(data=pca_result, columns=[f'PC{i}' for i in range(1, n_components + 1)])



# 输出前N个主成分的累计方差解释比例
cumulative_variance_ratio = sum(pca.explained_variance_ratio_[:n_components])
print(f'Cumulative Variance Explained by {n_components} Principal Components: {cumulative_variance_ratio:.2%}')

# 指定要绘制的主成分
selected_components = ['PC1', 'PC2']

# 可视化降维后的数据
plt.figure(figsize=(8, 6))
plt.scatter(pca_df[selected_components[0]], pca_df[selected_components[1]], alpha=0.5)
plt.xlabel(selected_components[0])
plt.ylabel(selected_components[1])
plt.title('PCA Visualization')
plt.show()

# 选择前m个主成分
m = 3  # 选择前5个主成分
selected_pca_df = pca_df.iloc[:, :m]
# 计算相关系数矩阵
correlation_matrix = selected_pca_df.corr()
# 绘制相关系数热力图
plt.figure(figsize=(8, 6))
sns.heatmap(correlation_matrix, annot=True, cmap="coolwarm", fmt=".2f")
plt.title(f'Correlation Heatmap of the First {m} Principal Components')
plt.show()

# 绘制前m个主成分之间的散点关系图
sns.pairplot(selected_pca_df)
plt.suptitle(f'Scatter Plot of the First {m} Principal Components')
plt.show()

3、PCA绘制二维图像与计算相关参数

import pandas as pd
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import seaborn as sns


# 读取CSV文件，header=None表示没有列标签
data = pd.read_csv('selected_data.csv', header=0)

# 提取特征（所有列）
features = data.iloc[:, :]

# 对特征进行标准化
scaler = StandardScaler()
scaled_features = scaler.fit_transform(features)

# 指定降维后的维度
n_components = 14  # 降维后的维度

# 创建PCA模型并进行降维
pca = PCA(n_components=n_components)
pca_result = pca.fit_transform(scaled_features)

# 将降维后的结果转换为DataFrame
pca_df = pd.DataFrame(data=pca_result, columns=[f'PC{i}' for i in range(1, n_components + 1)])

# 输出每一个主成分的方差解释比例
explained_variance_ratios = pca.explained_variance_ratio_
for i, explained_variance_ratio in enumerate(explained_variance_ratios, 1):
    print(f'Explained Variance Ratio for PC{i}: {explained_variance_ratio:.10%}')

# 输出前N个主成分的累计方差解释比例
cumulative_variance_ratio = sum(pca.explained_variance_ratio_[:n_components])
print(f'Cumulative Variance Explained by {n_components} Principal Components: {cumulative_variance_ratio:.2%}')

# 指定要绘制的主成分
selected_components = ['PC1', 'PC2']

# 创建一个新列，用于标识数据行所属的部分
pca_df['Group'] = None
pca_df.loc[0:16, 'Group'] = 'MF'  # 第一部分
pca_df.loc[16:32, 'Group'] = 'METH'  # 第二部分
pca_df.loc[32:48, 'Group'] = 'GE'  # 第三部分
pca_df.loc[48:64, 'Group'] = 'CNA'  # 第四部分

# 定义颜色映射
colors = {'MF': 'red', 'METH': 'blue', 'GE': 'green', 'CNA': 'purple'}

# 根据分组使用不同颜色绘制点
plt.figure(figsize=(8, 6))
for group, color in colors.items():
    group_data = pca_df[pca_df['Group'] == group]
    plt.scatter(group_data[selected_components[0]], group_data[selected_components[1]], c=color, label=group, alpha=0.5)

plt.xlabel(selected_components[0])
plt.ylabel(selected_components[1])
plt.title('PCA Visualization with Grouping')
plt.legend()
plt.show()

# 选择前m个主成分
m = 5
selected_pca_df = pca_df.iloc[:, :m]
selected_pca_df['Group'] = pca_df['Group']  # 包含 'Group' 列

"""# 绘制相关系数热力图
# 计算相关系数矩阵
correlation_matrix = selected_pca_df.corr()
plt.figure(figsize=(8, 6))
sns.heatmap(correlation_matrix, annot=True, cmap="coolwarm", fmt=".2f")
plt.title(f'Correlation Heatmap of the First {m} Principal Components')
plt.show()"""

# 绘制前m个主成分之间的散点关系图，并按组分配不同颜色
sns.pairplot(selected_pca_df, hue='Group', palette=colors)
plt.suptitle(f'Scatter Plot of the First {m} Principal Components')
plt.show()

#将PCA降维的结果保存，以便后续t-SNE的操作
# 将降维后的结果转换为DataFrame
pca_df = pd.DataFrame(data=pca_result, columns=[f'PC{i}' for i in range(1, n_components + 1)])
# 保存PCA降维后的数据到CSV文件
pca_df.to_csv('pca_processed.csv', index=False)

4、PCA绘制三维图像

import pandas as pd
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import seaborn as sns
from mpl_toolkits.mplot3d import Axes3D

# 读取CSV文件，header=0表示有列标签
data = pd.read_csv('selected_data.csv', header=0)

# 提取特征（所有列）
features = data.iloc[:, :]

# 对特征进行标准化
scaler = StandardScaler()
scaled_features = scaler.fit_transform(features)

# 指定主成分的数量
n_components = 3  # 3D图

# 创建PCA模型并进行降维
pca = PCA(n_components=n_components)
pca_result = pca.fit_transform(scaled_features)

# 将降维后的数据转换为DataFrame
pca_df = pd.DataFrame(data=pca_result, columns=[f'PC{i}' for i in range(1, n_components + 1)])

# 输出前三个主成分的方差解释比例
explained_variance_ratios = pca.explained_variance_ratio_
for i, explained_variance_ratio in enumerate(explained_variance_ratios, 1):
    print(f'主成分{i}的方差解释比例: {explained_variance_ratio:.10%}')

# 输出前三个主成分的累积方差解释比例
cumulative_variance_ratio = sum(pca.explained_variance_ratio_[:n_components])
print(f'前{cumulative_variance_ratio:.2%}的主成分累积方差解释比例')

# 创建一个新列，用于标识数据行所属的部分
pca_df['Group'] = None
pca_df.loc[0:16, 'Group'] = 'MF'  # 第一部分
pca_df.loc[16:32, 'Group'] = 'METH'  # 第二部分
pca_df.loc[32:48, 'Group'] = 'GE'  # 第三部分
pca_df.loc[48:64, 'Group'] = 'CNA'  # 第四部分

# 定义颜色映射
colors = {'MF': 'red', 'METH': 'blue', 'GE': 'green', 'CNA': 'purple'}

# 指定用于三维图的主成分
selected_components = ['PC1', 'PC2', 'PC3']

# 创建一个三维散点图
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# 根据“Group”分配不同颜色的数据点
for group, color in colors.items():
    group_data = pca_df[pca_df['Group'] == group]
    ax.scatter(group_data[selected_components[0]], group_data[selected_components[1]], group_data[selected_components[2]], c=color, label=group, alpha=0.5)

ax.set_xlabel(selected_components[0])
ax.set_ylabel(selected_components[1])
ax.set_zlabel(selected_components[2])
ax.set_title('PCA可视化三维图')
ax.legend(loc='upper left', bbox_to_anchor=(1.0, 1.0))  #调整图例位置
ax.legend()
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.show()

5、ICA绘制二维图像

import pandas as pd
from sklearn.decomposition import FastICA
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mutual_info_score
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from scipy.stats import kurtosis, skew  # 导入峰度和偏度函数

# 读取CSV文件，header=None表示没有列标签
data = pd.read_csv('selected_data.csv', header=0)

# 提取特征（所有列）
features = data.iloc[:, :]

# 对特征进行标准化
scaler = StandardScaler()
scaled_features = scaler.fit_transform(features)

# 指定降维后的维度
n_components = 3  # 降维后的维度

# 创建ICA模型并进行降维
ica = FastICA(n_components=n_components)
ica_result = ica.fit_transform(scaled_features)

# 将降维后的结果转换为DataFrame
ica_df = pd.DataFrame(data=ica_result, columns=[f'IC{i}' for i in range(1, n_components + 1)])

# 计算信噪比（SNR）
# 假设第一个独立成分是信号，剩下的成分是噪声
signal_component = ica_result[:, 0]
noise_components = ica_result[:, 1:]
snr = np.mean(np.abs(signal_component) / np.std(noise_components, axis=1))
print(f'Signal-to-Noise Ratio (SNR): {snr:.2f}')

# 指定要绘制的独立成分
selected_components = ['IC1', 'IC2']
# 创建一个新列，用于标识数据行所属的部分
ica_df['Group'] = None
ica_df.loc[0:16, 'Group'] = 'MF'  # 第一部分
ica_df.loc[16:32, 'Group'] = 'METH'  # 第二部分
ica_df.loc[32:48, 'Group'] = 'GE'  # 第三部分
ica_df.loc[48:64, 'Group'] = 'CNA'  # 第四部分
# 定义颜色映射
colors = {'MF': 'red', 'METH': 'blue', 'GE': 'green', 'CNA': 'purple'}
# 根据分组使用不同颜色绘制点
plt.figure(figsize=(8, 6))
for group, color in colors.items():
    group_data = ica_df[ica_df['Group'] == group]
    plt.scatter(group_data[selected_components[0]], group_data[selected_components[1]], c=color, label=group, alpha=0.5)
plt.xlabel(selected_components[0])
plt.ylabel(selected_components[1])
plt.title('ICA Visualization with Grouping')
plt.legend()
plt.show()

"""# 选择前m个独立成分
m = 5
selected_ica_df = ica_df.iloc[:, :m]
selected_ica_df['Group'] = ica_df['Group']  # 包含 'Group' 列
# 绘制前m个独立成分之间的散点关系图，并按组分配不同颜色
sns.pairplot(selected_ica_df, hue='Group', palette=colors)
plt.suptitle(f'Scatter Plot of the First {m} Independent Components')
plt.show()"""


# 计算互信息（Mutual Information）
# 假设第一个独立成分是信号，原始信号是真实信号
true_signal = scaled_features[:, 0]
mi = mutual_info_score(true_signal, signal_component)
print(f'Mutual Information (MI) with True Signal: {mi:.4f}')

# 计算峰度和偏度
kurtosis_values = kurtosis(ica_result, axis=0)
skewness_values = skew(ica_result, axis=0)

# 创建一个DataFrame来存储结果
result_df = pd.DataFrame({'Component': ica_df.columns[:-1], 'Kurtosis': kurtosis_values, 'Skewness': skewness_values})

# 打印结果
print(result_df)

6、ICA绘制三维图像

from mpl_toolkits.mplot3d import Axes3D  # 导入3D绘图库
import pandas as pd
from sklearn.decomposition import FastICA
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt


# 读取CSV文件，header=None表示没有列标签
data = pd.read_csv('selected_data.csv', header=0)

# 提取特征（所有列）
features = data.iloc[:, :]

# 对特征进行标准化
scaler = StandardScaler()
scaled_features = scaler.fit_transform(features)

# 指定降维后的维度
n_components = 3  # 降维后的维度

# 创建ICA模型并进行降维
ica = FastICA(n_components=n_components)
ica_result = ica.fit_transform(scaled_features)

# 将降维后的结果转换为DataFrame
ica_df = pd.DataFrame(data=ica_result, columns=[f'IC{i}' for i in range(1, n_components + 1)])

# 创建一个新列，用于标识数据行所属的部分
ica_df['Group'] = None
ica_df.loc[0:16, 'Group'] = 'MF'  # 第一部分
ica_df.loc[16:32, 'Group'] = 'METH'  # 第二部分
ica_df.loc[32:48, 'Group'] = 'GE'  # 第三部分
ica_df.loc[48:64, 'Group'] = 'CNA'  # 第四部分

# 定义颜色映射
colors = {'MF': 'red', 'METH': 'blue', 'GE': 'green', 'CNA': 'purple'}

# 选择要绘制的独立成分
selected_components = ['IC1', 'IC2', 'IC3']

# 创建一个新的三维图
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

# 根据分组使用不同颜色绘制点
for group, color in colors.items():
    group_data = ica_df[ica_df['Group'] == group]
    ax.scatter(group_data[selected_components[0]], group_data[selected_components[1]], group_data[selected_components[2]], c=color, label=group, alpha=0.5)

ax.set_xlabel(selected_components[0])
ax.set_ylabel(selected_components[1])
ax.set_zlabel(selected_components[2])
ax.set_title('ICA 3D Visualization with Grouping')
ax.legend()

plt.show()

7、UMAP绘制二维图像

import pandas as pd
import umap
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler

# 读取CSV文件，header=None表示没有列标签
data = pd.read_csv('selected_data.csv', header=0)

# 提取特征（所有列）
features = data.iloc[:, :]

# 对特征进行标准化
scaled_features = StandardScaler().fit_transform(features)

# 创建UMAP模型并进行降维
n_components = 2  # 降维后的维度
umap_model = umap.UMAP(n_neighbors=4, n_components=n_components)
umap_result = umap_model.fit_transform(scaled_features)

# 将降维后的结果转换为DataFrame
umap_df = pd.DataFrame(data=umap_result, columns=[f'UMAP{i}' for i in range(1, n_components + 1)])

# 指定要绘制的UMAP成分
selected_components = ['UMAP1', 'UMAP2']

# 创建一个新列，用于标识数据行所属的部分
umap_df['Group'] = None
umap_df.loc[0:16, 'Group'] = 'MF'  # 第一部分
umap_df.loc[16:32, 'Group'] = 'METH'  # 第二部分
umap_df.loc[32:48, 'Group'] = 'GE'  # 第三部分
umap_df.loc[48:64, 'Group'] = 'CNA'  # 第四部分

# 定义颜色映射
colors = {'MF': 'red', 'METH': 'blue', 'GE': 'green', 'CNA': 'purple'}

# 根据分组使用不同颜色绘制点
plt.figure(figsize=(8, 6))
for group, color in colors.items():
    group_data = umap_df[umap_df['Group'] == group]
    plt.scatter(group_data[selected_components[0]], group_data[selected_components[1]], c=color, label=group, alpha=0.5)

plt.xlabel(selected_components[0])
plt.ylabel(selected_components[1])
plt.title('UMAP Visualization with Grouping')
plt.legend()
plt.show()

8、UMAP绘制三维图像

import pandas as pd
import umap
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D  # 导入3D绘图模块
from sklearn.preprocessing import StandardScaler

# 读取CSV文件，header=None表示没有列标签
data = pd.read_csv('selected_data.csv', header=0)

# 提取特征（所有列）
features = data.iloc[:, :]

# 对特征进行标准化
scaled_features = StandardScaler().fit_transform(features)

# 创建UMAP模型并进行降维
n_components = 3  # 降维后的维度
umap_model = umap.UMAP(n_neighbors=4, n_components=n_components)
umap_result = umap_model.fit_transform(scaled_features)

# 将降维后的结果转换为DataFrame
umap_df = pd.DataFrame(data=umap_result, columns=[f'UMAP{i}' for i in range(1, n_components + 1)])

# 指定要绘制的UMAP成分
selected_components = ['UMAP1', 'UMAP2', 'UMAP3']  # 选择三个成分

# 创建一个新列，用于标识数据行所属的部分
umap_df['Group'] = None
umap_df.loc[0:16, 'Group'] = 'MF'  # 第一部分
umap_df.loc[16:32, 'Group'] = 'METH'  # 第二部分
umap_df.loc[32:48, 'Group'] = 'GE'  # 第三部分
umap_df.loc[48:64, 'Group'] = 'CNA'  # 第四部分

# 定义颜色映射
colors = {'MF': 'red', 'METH': 'blue', 'GE': 'green', 'CNA': 'purple'}

# 创建一个三维坐标轴
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

# 根据分组使用不同颜色绘制点
for group, color in colors.items():
    group_data = umap_df[umap_df['Group'] == group]
    ax.scatter(group_data[selected_components[0]], group_data[selected_components[1]], group_data[selected_components[2]], c=color, label=group, alpha=0.5)

ax.set_xlabel(selected_components[0])
ax.set_ylabel(selected_components[1])
ax.set_zlabel(selected_components[2])
ax.set_title('UMAP 3D Visualization with Grouping')
plt.legend()
plt.show()

9、t-SNE绘制二维图像

import pandas as pd
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
import seaborn as sns

# 读取CSV文件，header=None表示没有列标签
data = pd.read_csv('pca_processed.csv', header=0)

# 提取特征（所有列）
features = data.iloc[:, :]

# 创建t-SNE模型并进行降维
n_components = 2  # 降维后的维度
tsne_model = TSNE(n_components=n_components, random_state=7)
tsne_result = tsne_model.fit_transform(features)

# 将降维后的结果转换为DataFrame
tsne_df = pd.DataFrame(data=tsne_result, columns=[f't-SNE{i}' for i in range(1, n_components + 1)])

# 指定要绘制的t-SNE成分
selected_components = ['t-SNE1', 't-SNE2']

# 创建一个新列，用于标识数据行所属的部分
tsne_df['Group'] = None
tsne_df.loc[0:16, 'Group'] = 'MF'  # 第一部分
tsne_df.loc[16:32, 'Group'] = 'METH'  # 第二部分
tsne_df.loc[32:48, 'Group'] = 'GE'  # 第三部分
tsne_df.loc[48:64, 'Group'] = 'CNA'  # 第四部分

# 定义颜色映射
colors = {'MF': 'red', 'METH': 'blue', 'GE': 'green', 'CNA': 'purple'}

# 根据分组使用不同颜色绘制点
plt.figure(figsize=(8, 6))
for group, color in colors.items():
    group_data = tsne_df[tsne_df['Group'] == group]
    plt.scatter(group_data[selected_components[0]], group_data[selected_components[1]], c=color, label=group, alpha=0.5)

plt.xlabel(selected_components[0])
plt.ylabel(selected_components[1])
plt.title('t-SNE Visualization with Grouping')
plt.legend()
plt.show()

10、t-SNE绘制三维图像

import pandas as pd
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D  # 导入三维绘图工具
import seaborn as sns

# 读取CSV文件，header=None表示没有列标签
data = pd.read_csv('pca_processed.csv', header=0)

# 提取特征（所有列）
features = data.iloc[:, :]

# 创建t-SNE模型并进行降维
n_components = 3  # 降维后的维度
tsne_model = TSNE(n_components=n_components, random_state=7)
tsne_result = tsne_model.fit_transform(features)

# 将降维后的结果转换为DataFrame
tsne_df = pd.DataFrame(data=tsne_result, columns=[f't-SNE{i}' for i in range(1, n_components + 1)])

# 指定要绘制的t-SNE成分
selected_components = ['t-SNE1', 't-SNE2', 't-SNE3']

# 创建一个新列，用于标识数据行所属的部分（根据您的需求设置）
tsne_df['Group'] = None
tsne_df.loc[0:16, 'Group'] = 'MF'  # 第一部分
tsne_df.loc[16:32, 'Group'] = 'METH'  # 第二部分
tsne_df.loc[32:48, 'Group'] = 'GE'  # 第三部分
tsne_df.loc[48:64, 'Group'] = 'CNA'  # 第四部分

# 定义颜色映射
colors = {'MF': 'red', 'METH': 'blue', 'GE': 'green', 'CNA': 'purple'}

# 创建三维图像
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')  # 创建三维绘图区域

# 根据分组使用不同颜色绘制点
for group, color in colors.items():
    group_data = tsne_df[tsne_df['Group'] == group]
    ax.scatter(group_data[selected_components[0]], group_data[selected_components[1]],
               group_data[selected_components[2]], c=color, label=group, alpha=0.5)

ax.set_xlabel(selected_components[0])
ax.set_ylabel(selected_components[1])
ax.set_zlabel(selected_components[2])
ax.set_title('t-SNE 3D Visualization with Grouping')
plt.legend()
plt.show()

文章来源:https://blog.csdn.net/qq_39480177/article/details/135734669
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！

HNU-数据挖掘-实验2-数据降维与可视化

数据挖掘课程实验实验2 数据降维与可视化

文章目录

实验背景

实验目标

实验数据集说明

实验参考步骤

实验过程

1.对数据进行初步降维

2.使用无监督数据降维方法，比如PCA，ICA、UMap等进行降维

（1）主成分分析（PCA）降维

①基础知识

②评价指标

③可视化

★问题探究：改变n_components，PCA主成分并没有变化？

（2）独立成分分析（ICA）降维

①基础知识

②评价指标

③维度选择与可视化

（3）Umap降维

①基础知识

②重要参数

③可视化

3.使用t-SNE进行可视化

①基础知识

②可视化

附录：中间过程csv文件的解释

附录：代码

1、特征选择降维（预处理）代码

2、PCA基础代码

3、PCA绘制二维图像与计算相关参数

4、PCA绘制三维图像

5、ICA绘制二维图像

6、ICA绘制三维图像

7、UMAP绘制二维图像

8、UMAP绘制三维图像

9、t-SNE绘制二维图像

10、t-SNE绘制三维图像

数据挖掘课程实验
实验2 数据降维与可视化