【论文阅读笔记】Mip-NeRF 360: Unbounded Anti-Aliased Neural Radiance Fields

paper：https://arxiv.org/abs/2111.12077
code：https://github.com/google-research/multinerf
project：https://jonbarron.info/mipnerf360/

概述

MipNeRF360是在NeRF++和MipNeRF的基础上进行的扩展，利用NeRF++提出的远景参数化技巧和MipNeRF的低通滤波思想同时实现了无界场景的高质量渲染与抗锯齿。

摘要

1. 现有方法在新视角合成方面取得了令人影响深刻的结果
2. 但是现有方案由于附近和远处物体的细节和比例不平衡导致模糊和低分辨率渲染
3. 提出了基于mipnerf的扩展：场景参数化、在线蒸馏和一种失真正则化来克服抗锯齿和无界场景渲染
4. 目标场景是相机围绕一个点旋转360度的场景，同时能够得到较低的误差和更好的渲染质量、更详细的深度图

引言

1. NeRF（Neural Radiance Fields）使用沿着射线的无穷小3D点来建模多层感知机（MLP）的输入，这种建模方式在渲染不同分辨率的视图时可能会导致混叠现象
2. MipNeRF沿着截椎体进行推断，提高了质量但和NeRF一样都在渲染无界场景的时候遇到困难
3. 现有方法在处理无界场景的问题
   • 参数化：无界的360度场景可以占据一个任意大的欧几里德空间区域，但mip-NeRF要求3D场景坐标位于有界域内。
   • 效率：大型和详细的场景需要更多的网络容量，但在训练过程中沿着每条射线密集查询大型MLP是昂贵的。
   • 歧义性：无界场景的内容可能位于任意距离，并且只有少数射线观察到，加剧了从2D图像重建3D内容的固有歧义性

参数化

1. NeRF 成功的一个方面是它将特定场景类型与其适当的 3D 参数化配对，比如mask场景可直接在3D欧式空间进行参数化场景；对于前置场景，NeRF使用投影空间中定义的坐标(归一化设备坐标，或“NDC”）。通过将无限深的相机视锥体变形为有界的立方体，其中沿着z轴的距离对应视差（逆距离），NDC有效地重新分配了NeRF MLP的容量，以与透视投影的几何形状一致。
2. NeRF++ 使用一个额外的网络来模拟远处的对象；DONeRF 提出了一种空间扭曲过程，以将远处的点缩小到原点

效率

1. 随着场景的变大，MLP的容量也需要变大吗，带来了时间复杂度的增长
2. NeRF使用两个网络分别表达粗采样和细采样，但是粗采样对于最终图像没有贡献；本文使用了一个小型的proposal MLP和一个较大的NeRF MLP。proposal MLP预测体积密度，用于重新采样提供给NeRF MLP的新间隔，然后渲染图像。
3. proposal MLP生成的权重使用NeRF MLP生成的直方图权重进行监督，而不是输入图像。这使得能够使用一个大型的NeRF MLP，相对较少地进行评估，以及一个小型的提案MLP，进行更多次的评估。因此，整个模型的总容量比mip-NeRF的容量大得多（约15倍），从而显著提高了渲染质量，但我们的训练时间仅略有增加（约2倍）。
4. 两个MLP同时训练，被称为在线蒸馏。NeRV使用类似的建模可见性和光照，DONeRF使用深度图监督，TermiNeRF使用类似方案加速了推理，但减慢了训练
5. 几项工作尝试将训练好的NeRF**压缩或“烘焙”**成一个可以快速渲染的格式[KiloNeRF等]，但没有加速训练过程。在渲染领域，通过使用层次化数据结构（如八叉树或包围体层次结构）来加速光线追踪的思想已经得到了广泛探索，但这些方法假设对场景的几何形状有先验知识，因此无法自然地推广到逆向渲染的情景中，其中场景的几何形状是未知的，需要进行恢复。事实上，尽管在优化类似NeRF模型时构建了八叉树加速结构，但神经稀疏体素场方法并没有显著减少训练时间。

歧义性

1. 无限系列的nerf可以解释输入图像，但只有一个小子集为新视图产生可接受的结果。(参见nerf++)例如，一个NeRF可以通过将每个图像重新构建为其相应相机前方的纹理平面来重新创建所有输入图像
2. 原始的NeRF论文通过在NeRF MLP的密度头部在整流器之前注入高斯噪声来正则化模糊的场景这样可以使密度趋向于零或无穷大。尽管通过抑制半透明密度减少了一些"浮游物"，但我们将展示这对于我们更具挑战性的任务是不够的。其他的NeRF正则化方法也已经被提出，比如对密度的鲁棒损失或对表面的平滑惩罚[UNISURF,NeRFactor]，但这些解决方案解决的问题与我们的不同（渲染缓慢和非平滑表面）。此外，这些正则化方法是针对NeRF使用的点采样设计的，而我们的方法是为每个mip-NeRF射线上定义的连续权重而设计的。

mip-NeRF

使用位置集成编码对沿射线方向的圆锥台区间计算位置编码的均值和方差
$$\gamma (\mathbf{\mu },\mathbf{\Sigma })={\left\{\left[\begin{array}{l}\sin \left(2^{?}\mathbf{\mu }\right)\exp \left(?2^{2??1}\mathrm{diag}(\mathbf{\Sigma })\right)\\ \cos \left(2^{?}\mathbf{\mu }\right)\exp \left(?2^{2??1}\mathrm{diag}(\mathbf{\Sigma })\right)\end{array}\right]\right\}}_{?=0}^{L?1}$$

参考之前的文章：【论文阅读笔记】NeRF+Mip-NeRF+Instant-NGP

场景和光线参数化

根据一阶泰勒展开，可以将高斯函数的变换进行线性近似：
$$f(\mathbf{x})\approx f(\mathbf{\mu })+{\mathbf{J}}_f(\mathbf{\mu })(\mathbf{x}?\mathbf{\mu })$$
${\mathbf{J}}_f(\mathbf{\mu })$是在$\mathbf{\mu }$处的$f$的雅可比矩阵,
$$f(\mathbf{\mu },\mathbf{\Sigma })=\left(f(\mathbf{\mu }),{\mathbf{J}}_f(\mathbf{\mu })\mathbf{\Sigma }{\mathbf{J}}_f(\mathbf{\mu }{)}^{\mathrm{T}}\right)$$

这在功能上等同于经典的扩展卡尔曼滤波器，其中$f$是状态转移模型。我们选择的$f$如下所示的契约：
$$\mathrm{contract}(\mathbf{x})=\{\begin{array}{ll}\mathbf{x}& \Vert \mathbf{x}\Vert \le 1\\ \left(2?\frac{1}{\Vert \mathbf{x}\Vert }\right)\left(\frac{\mathbf{x}}{\Vert \mathbf{x}\Vert }\right)& \Vert \mathbf{x}\Vert >1\end{array}$$
这种设计与 NDC 具有相同的动机：远处的点应该按比例分布到视差（逆距离）而不是距离。

我们的场景参数化的二维可视化如上图所示。我们定义了一个契约（contract）算子（方程式10，用箭头表示），它将坐标映射到半径为2的球体（橙色区域），其中半径为1的点不受影响（蓝色区域）。我们将这个契约操作应用于欧几里得3D空间中的mip-NeRF高斯函数（灰色椭圆），类似于卡尔曼滤波器的作用，产生了我们的收缩高斯函数（红色椭圆），其中心保证位于半径为2的球体内。契约算子的设计结合我们根据视差线性间隔选择射线间隔的方式，意味着从位于场景原点的相机发出的射线在橙色区域具有等距离的间隔。

在NERF中，射线距离是通过从近平面和远平面均匀采样来完成。然而，如果使用NDC参数化，这种均匀间隔的样本序列实际上是在逆深度(视差)中均匀间隔的。当相机仅朝一个方向面对时，这种设计决策非常适合无界场景，但不适用于所有方向上无界的场景。因此，我们将明确地以视差线性采样我们的距离 t（有关此间距的详细动机，请参见 [Local Light Field Fusion: Practical View Synthesis with Prescriptive Sampling Guidelines、]）。为了根据视差参数化射线，我们定义了欧氏射线距离t和“归一化”射线距离s之间的可逆映射:
$$s?\frac{g(t)?g\left(t_n\right)}{g\left(t_f\right)?g\left(t_n\right)},t?g^{?1}\left(s?g\left(t_f\right)+(1?s)?g\left(t_n\right)\right)$$

通过设置$g(x)=1/x$并构建均匀分布在$s$空间中的射线样本，我们生成t距离在视差中线性分布的射线样本。这提供了映射到$[tn,tf]$ 的“归一化”射线距离 $s\in [0,1]$。

从粗到细的在线蒸馏

1. Mip-NeRF使用一个多尺度MLP，该MLP被反复查询(这里只显示两次重复)，用于下一阶段重新采样到间隔的权重，并监督所有尺度上产生的渲染
2. Mip-NeRF360使用“proposal MLP”来发出重新采样的权重（但不是颜色），在最后阶段，我们使用“NeRF MLP”来生成导致渲染图像的权重和颜色。训练proposal MLP 以产生与 NeRF MLP 的 w 输出一致的提案权重 $\hat{w}$。通过使用一个小的proposal MLP 和一个大的 NeRF MLP，可获得了一个高容量的组合模型，该模型仍然易于训练。这两个 MLP 都是随机初始化和联合训练的，因此这种监督可以被认为是 NeRF MLP 知识的一种“在线蒸馏”到proposal MLP
3. 这种在线蒸馏需要一个损失函数，它鼓励proposal MLP($\hat{t}$, $\hat{w}$) 和 NeRF MLP (t, w) 发出的直方图保持一致
4. 为此，我们首先定义一个函数，该函数计算与区间 $T$重叠的所有提议权重的总和：
   $$\mathrm{bound}(\hat{\mathbf{t}},\hat{\mathbf{w}},T)=\sum _{j:T\cap {\hat{T}}_j\ne ?}{\hat{w}}_j$$
   如果两个直方图彼此一致，则必须保持 $(t,w)$ 中所有区间 $(Ti,wi)$ 的 $w_i\le \mathrm{bound}(\hat{\mathbf{t}},\hat{\mathbf{w}},T_i)$
   $${\mathcal{L}}_{\text{prop?}}(\mathbf{t},\mathbf{w},\hat{\mathbf{t}},\hat{\mathbf{w}})=\sum \frac{1}{w}\max {\left(0,w_i?\mathrm{bound}\left(\hat{\mathbf{t}},\hat{\mathbf{w}},T_i\right)\right)}^2$$
   我们在计算 ${\mathcal{L}}_{\text{prop?}}$ 时对 NeRF MLP 的输出 t 和 w 放置一个停止梯度(stop-gradient)，以便 NeRF MLP 引到proposal MLP

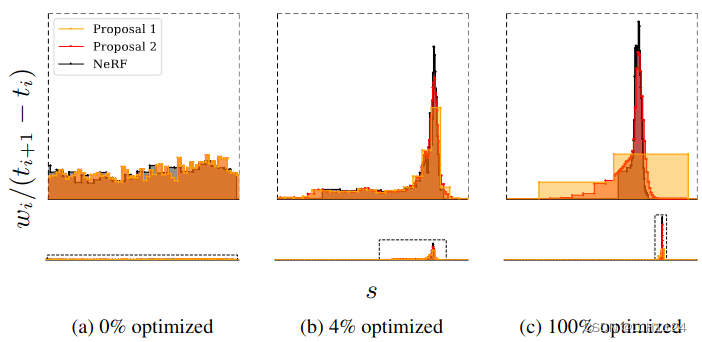
从NeRF MLP(黑色)发出的直方图(t, w)和建议MLP(黄色和橙色)发出的两组直方图(t, w)的可视化，用于来自我们的数据集自行车场景的每条射线在训练过程中。下面我们用固定的 x 和 y 轴可视化整个光线，但上面我们裁剪两个轴以更好地可视化场景内容附近的细节。直方图权重绘制为积分为 1 的分布。 (a) 在训练开始时，所有权重都相对于射线距离 t 均匀分布， (b, c)随着训练的进行，NeRF 权重开始集中在表面上，提案权重在这些 NeRF 权重周围形成一种包络。

基于区间的模型的正则化

我们的正则化器抑制了“漂浮物”（漂浮在空间中的半透明材料片段，这在深度图中很容易识别），并防止背景中的表面“塌陷”到相机的现象（如 (a) 左下角所示）。原始版本的NeRF的噪声注入方法只部分消除了这些伪影，降低了重建质量(注意远处树深度缺乏细节)。
我们的正则化器在由参数化每条射线的（归一化）射线距离 s 和权重 w 集定义的阶跃函数方面有一个直接的定义：
$$\begin{gathered} {\mathcal{L}}_{\text{dist?}}(\mathbf{s},\mathbf{w})={\int }_{?\infty }^{\infty }{\int }_{{\mathbf{w}}_{\mathbf{s}}}(u){\mathbf{w}}_{\mathbf{s}}(v)|u?v|d_u{d}_v \\ {\mathbf{w}}_{\mathbf{s}}(u)=\sum _i{w}_i{1}_{\left[s_i,s_{i+1}\right)}(u) \end{gathered}$$

简单理解就是为了让单一射线上的权重分布更接近于脉冲阶跃函数

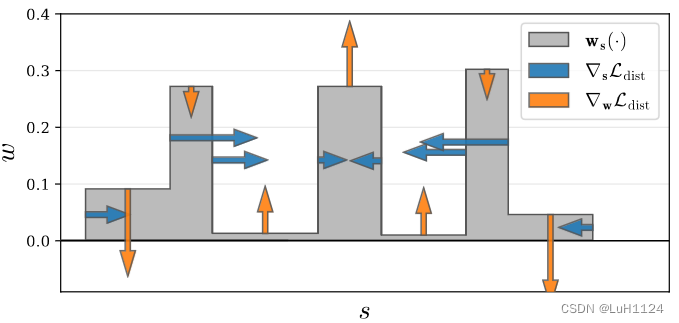
$?{\mathcal{L}}_{\text{dist?}}$的可视化，作为s和w的函数在一个阶跃函数上。我们的损失函数鼓励每个射线尽可能紧凑，方法有：1）最小化每个间隔的宽度，2）将远距离的间隔拉近，3）将权重集中到一个间隔或附近的少数几个间隔，4）在可能的情况下将所有权重推向零（例如当整个射线未被占用时）。

由于 ws(·) 在每个区间内都有一个常数值，正则化可重写为：
$$\begin{array}{rl}{\mathcal{L}}_{\text{dist?}}(\mathbf{s},\mathbf{w})& =\sum _{i,j}{w}_i{w}_j\left|\frac{s_i+s_{i+1}}{2}?\frac{s_j+s_{j+1}}{2}\right|+\frac{1}{3}\sum w_i^2\left(s_{i+1}?s_i\right)\end{array}$$
第一项最小化所有区间中点对之间的加权距离（使得区间越来越小），第二项最小化每个单独区间的加权大小（使得不同区间的w越来越小）

实现细节

使用具有 4 层和 256 个隐藏单元的proposal MLP 和具有 8 层和 1024 个隐藏单元的 NeRF MLP，这两者都使用 ReLU 内部激活和密度$\tau$的 softplus 激活。我们使用 64 个样本对每个提议 MLP 进行两个阶段的评估和重采样以产生 (${\hat{s}}^0$, ${\hat{w}}^0$) 和 (${\hat{s}}^1$, ${\hat{w}}^1$)，然后使用 32 个样本评估 NeRF MLP 的一个阶段以产生 (s, w)。我们最小化以下损失：
$${\mathcal{L}}_{\text{recon?}}\left(\mathbf{C}(\mathbf{t}),{\mathbf{C}}^{?}\right)+\lambda {\mathcal{L}}_{\text{dist?}}(\mathbf{s},\mathbf{w})+\sum _{k=0}^1{\mathcal{L}}_{\text{prop?}}\left(\mathbf{s},\mathbf{w},{\hat{\mathbf{s}}}^k,{\hat{\mathbf{w}}}^k\right)$$
对于${\mathcal{L}}_{recon}=\sqrt{{\left(x?x^{?}\right)}^2+{?}^2}\text{?with?}?=0.001$

实验

场景设置：在捕获过程中，通过固定相机曝光设置、最小化光照变化和避免移动物体来防止光度变化，我们不打算探索“在野外”照片集合 [NeRF in the Wild: Neural Radiance Fields for Unconstrained Photo Collections ]

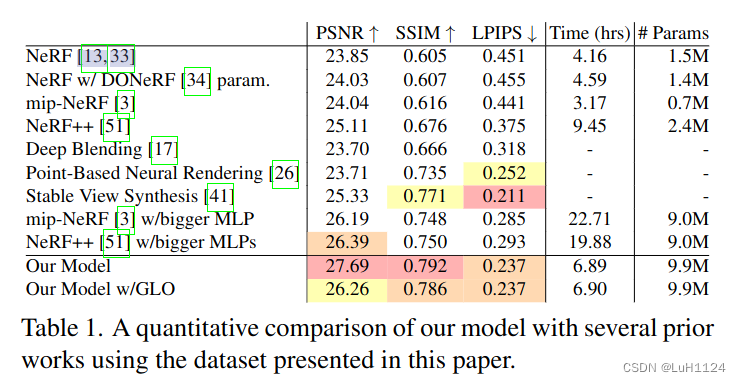
• 和其他SOTA方法的对比：
  
• 消融实验：
  
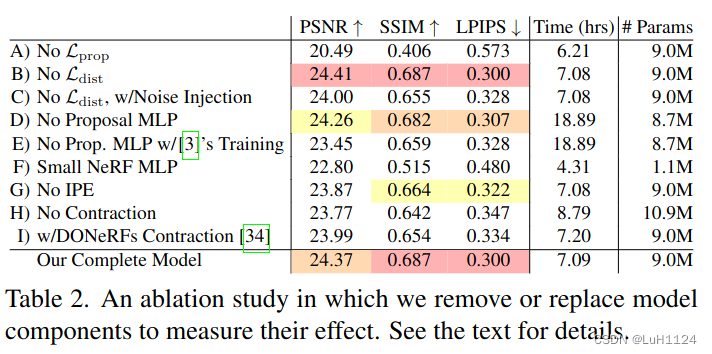
  其中I)使用DONeRF[34]中提出的参数化和对数射线，降低了精度。

限制

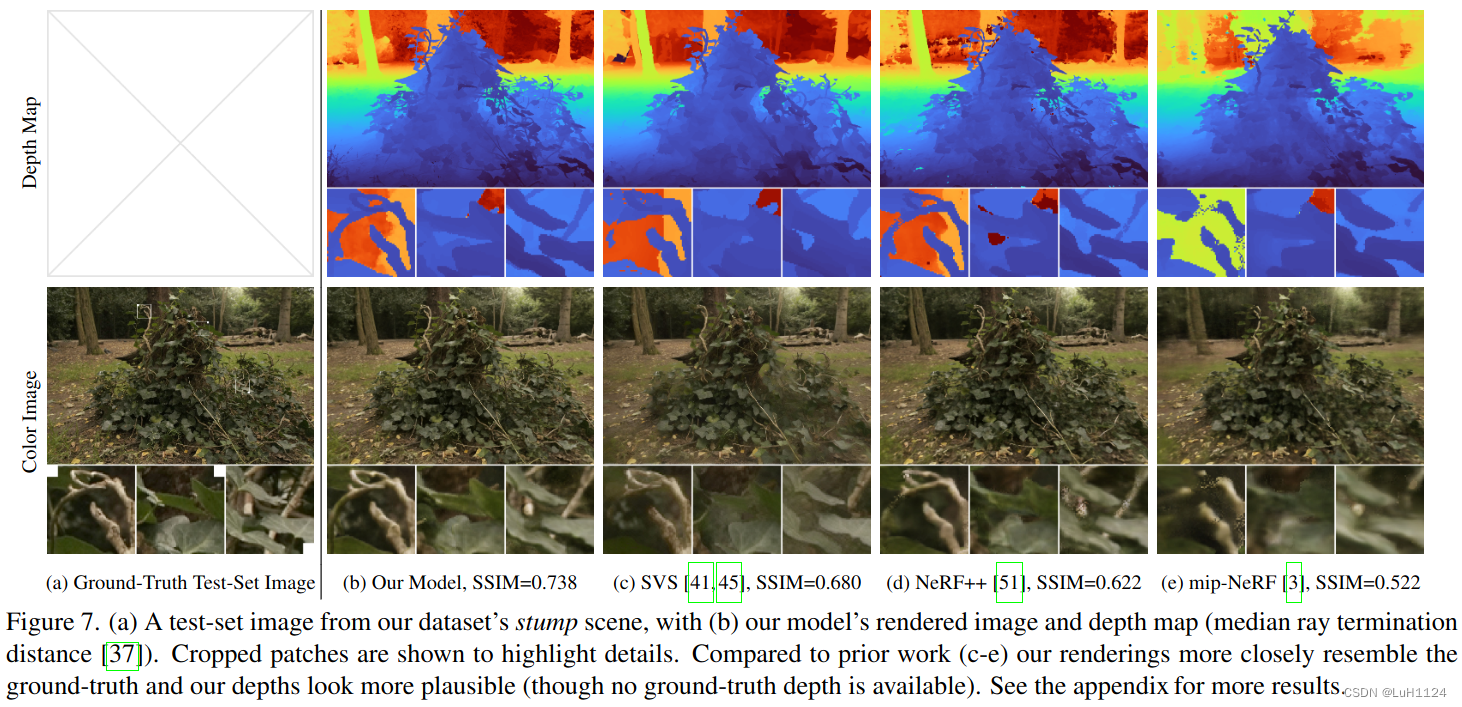
尽管 mip-NeRF 360 显着优于 mip-NeRF 和其他先前的工作，但它并不完美。可能会遗漏一些薄的结构和精细细节，例如自行车场景中的轮胎辐条（图 5）或倾倒场景中的叶子上的静脉（图 7）。如果相机远离场景的中心，视图合成质量可能会下降。而且，与大多数类似 NeRF 的模型一样，恢复场景需要对加速器进行几个小时的训练，排除了设备上的训练。

总结：

1. 使用一种新颖的类卡尔曼场景参数化
2. 一种高效的基于提议的粗到细蒸馏框架
3. 为 mipNeRF 射线间隔设计的正则化器

附录

一些有意思的点
###非轴对齐编码

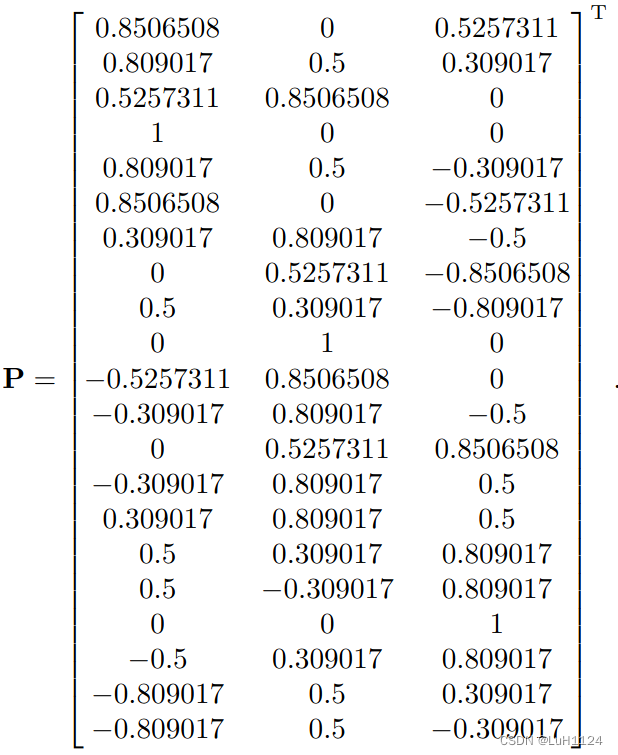
1. 在构建集成位置编码特征时，我们必须选择一个基底P。在mip-NeRF中，这个基底被选为单位矩阵。这是方便的，因为这意味着只需要对角线上的协方差矩阵Σ来构建IPE特征，而不需要计算非对角线分量。然而，我们模型使用的重新参数化需要访问完整的协方差矩阵，否则我们使用的类似卡尔曼滤波的变形在场景中高度各向异性的高斯函数（在场景的远处经常出现）存在时会不准确。因此，考虑到我们需要构建一个完整的Σ矩阵，我们利用其中提供的额外信息，并编码不仅仅是轴对齐的IPE特征，还包括非轴对齐的IPE特征。作为我们的基底P，我们使用了一个大而瘦的矩阵，其中包含了一个二次细分的二十面体的单位规范顶点，同时删除了冗余的负顶点副本。为了重现的目的，这个矩阵是：
   
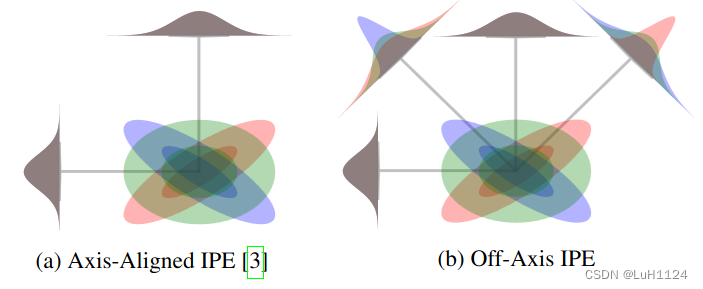
   mipNeRF中使用的轴对齐位置编码不能捕捉到所编码的高斯函数的协方差。在这里，我们绘制了三个双变量高斯函数，用红色、绿色和蓝色表示，其中(a)是使用轴对齐IPE，而**(b)是使用我们的非轴对齐IPE**。我们还展示了通过将每个高斯函数投影到每个编码使用的基础上产生的边缘分布。因为这些高斯函数具有相同的边缘分布，mip-NeRF的轴对齐IPE产生相同的特征，而我们方法的非轴对齐投影可以将它们区分开来。
2. 使用mip-NeRF中描述的过程计算具有大的P矩阵的IPE特征（diag(PΣPT)）是非常昂贵的。一个可行的替代方案是计算等效表达式sum(PT ? (ΣPT), 0)，其中?是逐元素乘积，sum(·, 0)是对行进行求和。通过这个小优化，非轴对齐的IPE特征的计算成本只比mip-NeRF中使用的轴对齐的IPE特征略高。

退火

在从proposal权重$\hat{w}$重新采样射线区间之前，我们通过将这些权重提升到某个幂次来退火这些权重。在N个训练步骤中，在第n步我们计算：
$${\hat{\mathbf{W}}}_n\propto {\hat{\mathbf{W}}}^{\frac{bn/N}{(b?1)n/N+1}}$$

"退火"是指通过对权重进行幂次操作来调整它们的值。这个操作的目的是在训练过程中逐渐降低权重的影响力，以便更好地控制采样的过程。 但这个权重是谁，我在研究下代码（ToDo）

膨胀

在对每个建议直方图（$\hat{t}，\hat{w}$）进行重新采样之前，我们会稍微"膨胀"它们。这样做可以减少混叠伪影，可能是因为建议MLP只使用与输入像素对应的射线进行监督训练，因此其预测可能仅适用于特定角度——从某种意义上说，建议网络存在旋转混叠伪影。通过扩大建议MLP的区间，我们有助于抵消这种混叠伪影。为了膨胀直方图（?s，?w），我们首先计算?p，其中?pi = ?wi / (?si+1 ? ?si)，这给我们一个概率密度，其积分为1，而不是和为1的直方图。然后，我们通过计算来膨胀这个概率密度：

采样

背景颜色