搜索专题-深度搜索

概念

深度优先搜索(Depth-First-Search，DFS)类似于树的先序遍历。DFS的基本思想如下：首先访问图中某一起始顶点v，然后由v出发，访问与v邻接且未被访问的任一顶点w1，再访问与w1邻接且未被访问的任一顶点w2……不断重复上述过程，当不能再继续向下访问时，依次回退到最近刚被访问的顶点，若它还有邻接顶点未被访问过，则从该点开始继续上述搜索过程，直至图中所有顶点均被访问过为止。

我们可以通过下面的动图加深理解。

模板

bool visited[MaxVertexNum]; //标记数组，用于指示每个顶点是否已被访问
void DFSTraverse(Graph G){ //对图G进行深度优先遍历
    for(int i=0;i<G.vexnum;i++)
        visited[i]=False; //初始化标记数组
    for(int i=0;i<G.vexnum;i++) //从0号顶点开始遍历
        if(!visited[i]) //对每个连通分量调用一次DFS
            DFS(G,i); //若顶点i未被访问，则从顶点i开始调用一次DFS
}
void DFS(Graph G,int v){ //从图G中的顶点v出发，深度优先遍历图G
    visit(v); //访问初始顶点v
    visited[v]=true; //对顶点v做已访问标记
    for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w)) //检查顶点v的所有邻接点
        if(!visited[w]) //若w为v的尚未访问的邻接顶点
            DFS(G,w); //若顶点w未被访问，则从w开始调用一次DFS
}

? 算法的时间复杂度为 O(n+e）

在深度优先搜索中，对搜索的状态而言，获得一个状态后，同样立即扩展这个状态，但需要保证早得到的状态较后得到扩展。这种先入后出的特点让人想到了栈这种数据结构，不过递归策略也能保证这一特性。考虑到递归的代码比较简洁明了，因此常常使用递归策略来求解深度优先搜索问题。

由于深度优先搜索并没有先入先出的特点，所以搜索到需要的状态时，该状态不再像是在宽度优先搜索中的状态一样，具有某种最优的特性。因此，使用深度优先搜索策略时，常常是为了知道问题是否有解，而一般不使用深度优先搜索求解最优解问题。

OJ练习

迷宫可行路径数问题

题目链接

题目描述

现有一个n*m大小的迷宫，其中1表示不可通过的墙壁，0表示平地。每次移动只能向上下左右移动一格（不允许移动到曾经经过的位置），且只能移动到平地上。求从迷宫左上角到右下角的所有可行路径的条数。

输入描述

输出描述

一个整数，表示可行路径的条数。

样例

样例1

输入

3 3
0 0 0
0 1 0
0 0 0

输出

2

解释

题解

对于这个问题，首先起始位置为（1，1），终止位置为（n,m）。这是左上角和右上角的坐标，我们对该图进行深度优先遍历，在遍历中，我们需要不断进行检测，判断下一步是否能走？并且下一个位置是否已经访问过？所以这里我们需要两个二维数组，第一个a数组，用于记录每个位置的信息，判断是平地还是有围墙，第二个visit数组，用于记录是否已经访问过。在dfs时，如果走到终点，那么进行回溯，往后退一步，如果上一步没有其他能走的地方了，那么就再回退，一直回退到无法回退为止。

那么首先进行数据初始化

int m,n,sum = 0;
int a[7][7] ;
int visit[7][7] ;

m和n分别代表宽高，a用于记录地形信息，visit判断是否已访问。

由于本题中1是有围墙，所以我们需要把a数组初始化全为1。

注意：不可以直接int a[7][]7 = 1，这样只有第一个元素被初始化为1，其他的还是0.

for(int i=0;i<=6;i++){
		for(int j=0;j<=6;j++){
			a[i][j] = 1;
		}
	}

所以我们只能使用for循环进行初始化，或者你可以使用fill函数。

接下来就要进行深度搜索遍历，在深度搜索前，我们先确定一个顺序，即顺时针进行搜索，右 下 左 上这个顺序。

我们递归结束的条件为

if(x==n&&y==m){
		sum++;
		return;
	}

可能有朋友还会问，我们dfs时候还要不要检查数组越界？因为可能出现当前遍历的结点在最上面或者最下面最右边最左边的情况，这样下次遍历的节点会不会已经出去了？我们的答案是不需要，因为我对数组初始化时候，我们是从0开始，而我们使用数组只从1开始，这样相当于我们有一个数组，但是最外面这一层我们是不用的，并且我们在初始化时候已经设置为墙壁，那么根本就进入不了我们的递归，所以这里节省掉了这一步骤。那么接下来就是四个方向逐个遍历，并且遍历完之后我们需要return。

void dfs(int x,int y){
	if(x==n&&y==m){
		sum++;
		return;
	}
	if(a[x][y+1]==0 && visit[x][y+1]==0 ){
		visit[x][y+1] = 1;
		dfs(x,y+1);
		visit[x][y+1] = 0;
	}
	if(a[x+1][y]==0 && visit[x+1][y]==0 ){
		visit[x+1][y] = 1;
		dfs(x+1,y);
		visit[x+1][y] = 0;
	}
	if(a[x][y-1]==0 && visit[x][y-1]==0 ){
		visit[x][y-1] = 1;
		dfs(x,y-1);
		visit[x][y-1] = 0;
	}
	if(a[x-1][y]==0 && visit[x-1][y]==0 ){
		visit[x-1][y] = 1;
		dfs(x-1,y+1);
		visit[x-1][y] = 0;
	}
	return;
}

这样我们的完整代码就搞定了。

#include<bits/stdc++.h>
using namespace std;
int m,n,sum = 0;
int a[7][7] ;
int visit[7][7] ;

void dfs(int x,int y){
	if(x==n&&y==m){
		sum++;
		return;
	}
	if(a[x][y+1]==0 && visit[x][y+1]==0 ){
		visit[x][y+1] = 1;
		dfs(x,y+1);
		visit[x][y+1] = 0;
	}
	if(a[x+1][y]==0 && visit[x+1][y]==0 ){
		visit[x+1][y] = 1;
		dfs(x+1,y);
		visit[x+1][y] = 0;
	}
	if(a[x][y-1]==0 && visit[x][y-1]==0 ){
		visit[x][y-1] = 1;
		dfs(x,y-1);
		visit[x][y-1] = 0;
	}
	if(a[x-1][y]==0 && visit[x-1][y]==0 ){
		visit[x-1][y] = 1;
		dfs(x-1,y+1);
		visit[x-1][y] = 0;
	}
	return;
}

int main(){
	cin >> n >> m;
	for(int i=0;i<=6;i++){
		for(int j=0;j<=6;j++){
			a[i][j] = 1;
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin >> a[i][j];
		}
	}
	visit[1][1] = 1;
	dfs(1,1);
	cout << sum;
	return 0;
}

但是我们会发现，上面的代码非常冗余，我们是不是可以进一步优化？

就比如顺时针遍历的时候，我们是不是可以定义一个方向数组，这样就能减少相同代码的重复。

int dx[4] = {0,1,0,-1};
int dy[4] = {1,0,-1,0};

我们有了方向数组，那么右下左上是不是就只是循环四次，然后每次我们取出方向数组对应移动方向，这样就可以完成遍历。

for(int i=0;i<=3;i++){
		int tx = x+dx[i],ty = y+dy[i];
		if(a[tx][ty] == 0 && visit[tx][ty] == 0){
			visit[tx][ty] = 1;
			dfs(tx,ty);
			visit[tx][ty] = 0;
		}
	}

现在的完整代码

#include<bits/stdc++.h>
using namespace std;
int m,n,sum = 0;
int a[7][7] ;
int visit[7][7] ;
int dx[4] = {0,1,0,-1};
int dy[4] = {1,0,-1,0};


void dfs(int x,int y){
	if(x==n&&y==m){
		sum++;
		return;
	}
	for(int i=0;i<=3;i++){
		int tx = x+dx[i],ty = y+dy[i];
		if(a[tx][ty] == 0 && visit[tx][ty] == 0){
			visit[tx][ty] = 1;
			dfs(tx,ty);
			visit[tx][ty] = 0;
		}
	}
	return;
}

int main(){
	cin >> n >> m;
	for(int i=0;i<=6;i++){
		for(int j=0;j<=6;j++){
			a[i][j] = 1;
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin >> a[i][j];
		}
	}
	visit[1][1] = 1;
	dfs(1,1);
	cout << sum;
	return 0;
}

指定步数的迷宫问题

指定步数的迷宫问题

题目描述

现有一个n*m大小的迷宫，其中1表示不可通过的墙壁，0表示平地。每次移动只能向上下左右移动一格（不允许移动到曾经经过的位置），且只能移动到平地上。现从迷宫左上角出发，问能否在恰好第步时到达右下角。

输入描述

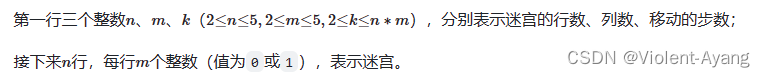
输出描述

如果可行，那么输出Yes，否则输出No。

样例

样例1

输入

3 3 4
0 1 0
0 0 0
0 1 0

输出

Yes

解释

样例2

输入

3 3 6
0 1 0
0 0 0
0 1 0

输出

No

解释

由于不能移动到曾经经过的位置，因此无法在恰好第6步时到达右下角。

题解

这个题就是在上一个题目的基础上加以改编，那么我们还是使用dfs但是这次我们dfs需要增加一个形参，step，step用于记录我们到达终点的步数，我们在递归结束的条件上加上一个如果step等于我们输入的那个k，那么此时说明找到了，应该返回yes，否则返回no

#include<bits/stdc++.h>
using namespace std;
int m,n,sum = 0,flag = 0,k;
int a[7][7] ;
int visit[7][7] ;
int dx[4] = {0,1,0,-1};
int dy[4] = {1,0,-1,0};


void dfs(int x,int y,int step){
	if(x==n&&y==m&&step==k){
		flag = 1;
		return;
	}
	for(int i=0;i<=3;i++){
		int tx = x+dx[i],ty = y+dy[i];
		if(a[tx][ty] == 0 && visit[tx][ty] == 0){
			visit[tx][ty] = 1;
			dfs(tx,ty,step+1);
			visit[tx][ty] = 0;
		}
	}
	return;
}

int main(){
	cin >> n >> m >> k;
	for(int i=0;i<=6;i++){
		for(int j=0;j<=6;j++){
			a[i][j] = 1;
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin >> a[i][j];
		}
	}
	visit[1][1] = 1;
	dfs(1,1,0);
	string res = flag == 1?"Yes":"No";
	cout << res;
	return 0;
}

下次文章中我会增加几个中等难度和困难的题目，那么我们下次见。