Datawhale 强化学习笔记(四）结合策略梯度和价值函数的 Actor-Critic 算法

策略梯度算法的缺点

• 采样效率低。由于使用的是蒙特卡洛估计，与基于价值算法的时序差分估计相比其采样速度必然是要慢很多的，这个问题在前面相关章节中也提到过。
• 高方差。虽然跟基于价值的算法一样都会导致高方差，但是策略梯度算法通常是在估计梯度时蒙特卡洛采样引起的高方差，这样的方差甚至比基于价值的算法还要高。
• 收敛性差。容易陷入局部最优，策略梯度方法并不保证全局最优解，因为它们可能会陷入局部最优点。策略空间可能非常复杂，存在多个局部最优点，因此算法可能会在局部最优点附近停滞。
• 难以处理高维离散动作空间：对于离散动作空间，采样的效率可能会受到限制，因为对每个动作的采样都需要计算一次策略。当动作空间非常大时，这可能会导致计算成本的急剧增加。

结合了策略梯度和值函数的 Actor-Critic 算法则能同时兼顾两者的优点，并且甚至能缓解两种方法都很难解决的高方差问题。
基于价值的（或称评论员型，Critic）, 基于策略的（或称 演员型）

高方差的来源

• 策略梯度算法是因为直接对策略参数化，相当于既要利用策略去与环境交互采样，又要利用采样去估计策略梯度
• 基于价值的算法也是需要与环境交互采样来估计值函数的，因此也会有高方差的问题。
  结合之后， Actor 部分还是负责估计策略梯度和采样，但 Critic 即原来的价值函数部分就不需要采样而只负责估计值函数了，并且由于它估计的值函数指的是策略函数的值，相当于带来了一个更稳定的估计，来指导 Actor 的更新，反而能够缓解策略梯度估计带来的方差。当然尽管 Actor-Critic 算法能够缓解方差问题，但并不能彻底解决问题。

Q Actor-Critic 算法

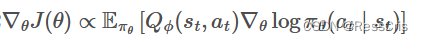
$Q_{?}(s_t,a_t)$ 输入是状态和动作，估计当前的值。输出的是单个值。
$?$ 表示 Critic 网络的参数。

Actor 策略函数 Policy
Critic 价值函数 Value Function
分别用两个模块来表示。
Actor 与环境交互采样，然后将采样的轨迹输入Critic 网络，Critic 网络估计出当前状态-动作对的价值，然后将价值作为 Actor 网络的梯度更新的依据。

优势函数，A2C， A3C

为了进一步缓解高方差问题，引入一个优势函数 $A^{pi}(s_t,a_t)$, 表示当前状态-动作相对于平均水平的优势。

原先的 A2C 算法相当于只有一个全局网络并持续与环境交互更新。而 A3C 算法中增加了多个进程，每一个进程都拥有一个独立的网络和环境以供交互，并且每个进程每隔一段时间都会将自己的参数同步到全局网络中，这样就能提高训练效率。

广义优势估计(待填坑)

时序差分