基于格密码的无线通信MIMO系统

目录

一. 系统模型

二. MIMO从复数到实数

三. MIMO星座图与格密码

四. 格密码与极大似然译码

五. 格基约化算法

六. 基于格密码的串行干扰消除算法

---

无线通信领域的MIMO可以等效成格密码中的解码问题，本文章将解释两者的关系。

一. 系统模型

MIMO?multi-input multi-ioutput 多天线输入多输出

假定某MIMO系统的发射端有根天线，接收端有根天线，如果该无线通信模型是平坦衰落的（flat fading），那么接收端Y可计算为：

（1）发射信号X

X代表发射信号，一共发射了T个时隙，所以：

发射信号X需要满足功率限制，比如可以将平均功率限定为1，那么可得：

（2）接受信号Y

Y代表接收信号，接收时隙也为T，所以：

（3）噪声N

噪声N的维度与Y永远是一样的，所以：

噪声矩阵中的每个元素都服从复高分布，均值为0，方差为。发射功率为1，所以可得信噪比SNR为：

（4）信道矩阵H

信道增益矩阵H的行代表接收天线，列代表发射天线，所以：

单独看信道矩阵的行和列，行满秩，列也满秩。在理想模型下，该矩阵中的元素均是独立同分布的，并且统计信息提前已知，为复高斯分布.要保证接收天线能译码出每个发射信号，则要求接收天线数大于发射天线数，也就是，从解方程的角度来看也就是方程个数不能少于变量的个数。

二. MIMO从复数到实数

通常MIMO会采用空时分组码（space-time block code），发射信号X是如何从调制信号转变而来的呢？

假定调制方式为QAM，维度为，可以将其看成一个向量。接着有一个生成矩阵G，是方阵，阶数为，由此发射向量s可以计算为：

也就是将X进行向量化便可以得到s。

将MIMO模型中的每个矩阵都进行向量化，也就是矩阵的第二列叠加在第一列的下面，以此类推。对接收信号Y进行向量化：

对噪声N进行向量化：

由此MIMO系统模型可以变成：

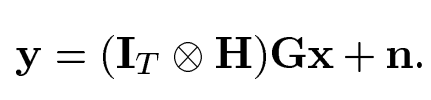
如果发射时隙为1，也就是T=1且生成矩阵为单位阵，也就是：

那么MIMO通信模型就是常见的：

因为该模型中的每个元素都是复数，所以可以分成实部和虚部，由此可得：

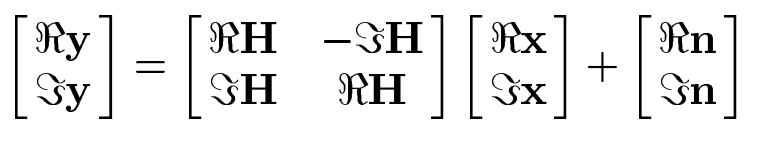
如果将复数模型等效成实数模型的话，其实就相当于发射天线为，接收天线为。如果考虑时隙T的话，那么该模型为：

三. MIMO星座图与格密码

综上实数域的MIMO系统就出现了，维度为。同样的，也要求。该模型如下：

其中B为m行n列的矩阵，也就是，根据以上讨论我们知道：

其中a为功率归一化因子。该信道矩阵的维度满足：

x为发射数据向量，为n维，可以假定从有限子集中取得。

如果把以上过程反映在MIMO的星座图中，比如我们选择M-QAM调制方式，那么A的取值则是：

将发射信号x看成整数格点的子集，那么Hx就相当于对整数格点进行放缩（scaled），Hx+e将相当于对格点进行平移，所以最终的结果就是我们常说的QAM星座图：

该格为m维。在欧几里得空间内，对线性独立的向量进行整数倍组合则可以形成格的概念，如下：

其中Z代表整数，B代表格L的格基，也就是：

如果把格点写成矩阵的形式，则如下：

需要注意的是，格基是存在无数个的。把格基B做幺模矩阵变换则可以得到一个新的格基B'，如下：

其中U为整数幺模矩阵，其行列式为正负1，

四. 格密码与极大似然译码

根据以上讨论可以把Bx看成一个格点，那么就可以利用格理论来进行MIMO系统的解码。例如，极大似然译码（ML）的本质是：

注意x的取值范围是在集合A内的，所以该问题相等于在格L的子集上解决最近向量问题（closest vector problem,CVP）。已有的知识告诉我们极大似然译码可以根据球形译码理论来解决，但是在固定信噪比SNR的情况下，球形译码的复杂度是指数的。

如何降低此复杂度？

可以暂时将以上有限的格点放宽到无限格上，那么就更好解决，如下：

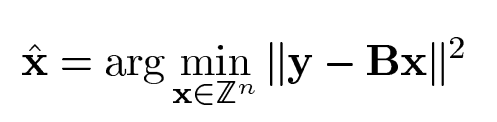
现在就可以使用格基约化等辅助手段来解决，这个过程又被称之为无限格译码算法（infinite lattice decoding, ILD）.需要注意的是，解出来的格点需要核对是否在星座图上。

五. 格基约化算法

格基约化算法主要是把一个格基B转化为正交性更加良好的向量，如下B':

其中U为幺模矩阵，于是可以得到如下等效信道模型：

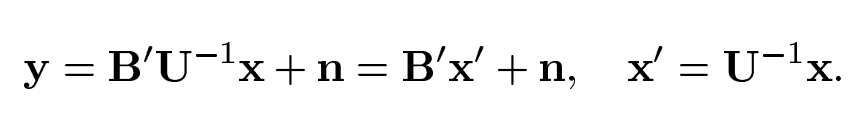
接下来就可以直接使用迫零算法和串行干扰消除算法，来解码出x。接着运算：

其中B'可以看成等效信道。当发现时，则需要重新把映射到有限格中。

六. 基于格密码的串行干扰消除算法

Babai最先提出格基约化算法，在这里我们把格密码理论和网络安全理论做一个联系：

格密码的舍入（round off）算法等效于无线通信中的迫零算法；

格密码的最近平面算法（nearest plane algorithm）等效于无线通信中的串行干扰消除（SIC）；

串行干扰消除的第一步是对信道矩阵进行QR分解：

其中Q为正交阵，代表列向量互相正交；

R为上对角阵，且对角线处的元素均为正数。

原MIMO模型如下：

两边同时乘以矩阵Q的伪逆，可得：

串行干扰消除算法是先从最后一个元素开始计算的，也就是:

对于来讲，对应的项则为干扰项。所以可以将其带入中，从而估计出

以此类推直至解出n个变量，该迭代过程可总结为：

注意是逆向求解，所以