Wilcoxon秩和检验-校正P值（自备）

R语言 boxplot作图 图内展示校正后的P值(padj)_r语言 p值校正-CSDN博客?

FDR错误发现率-P值校正学习_fdr和p值的关系-CSDN博客

原理介绍：

Benjamini-Hochberg 方法介绍

有N次假设检验，对每一次假设检验都计算其P值，然后将计算出的P值按照从小到大的方式排序，接着从最小的P值开始，按照P（k）≤α*k/N进行比较，然后可以找到最大的第K个满足上述不等式的P值，最终可以认为这K个P值是显著的，其余的P值不显著。

Benjamini-Hochberg方法原理

我们将10000次假设检验分为2组：

1. 9000次检验的零假设H0：真；
2. 1000次检验的零假设H0：假。

然后，可以看到这两组检验的P值分布情况如下图所示：

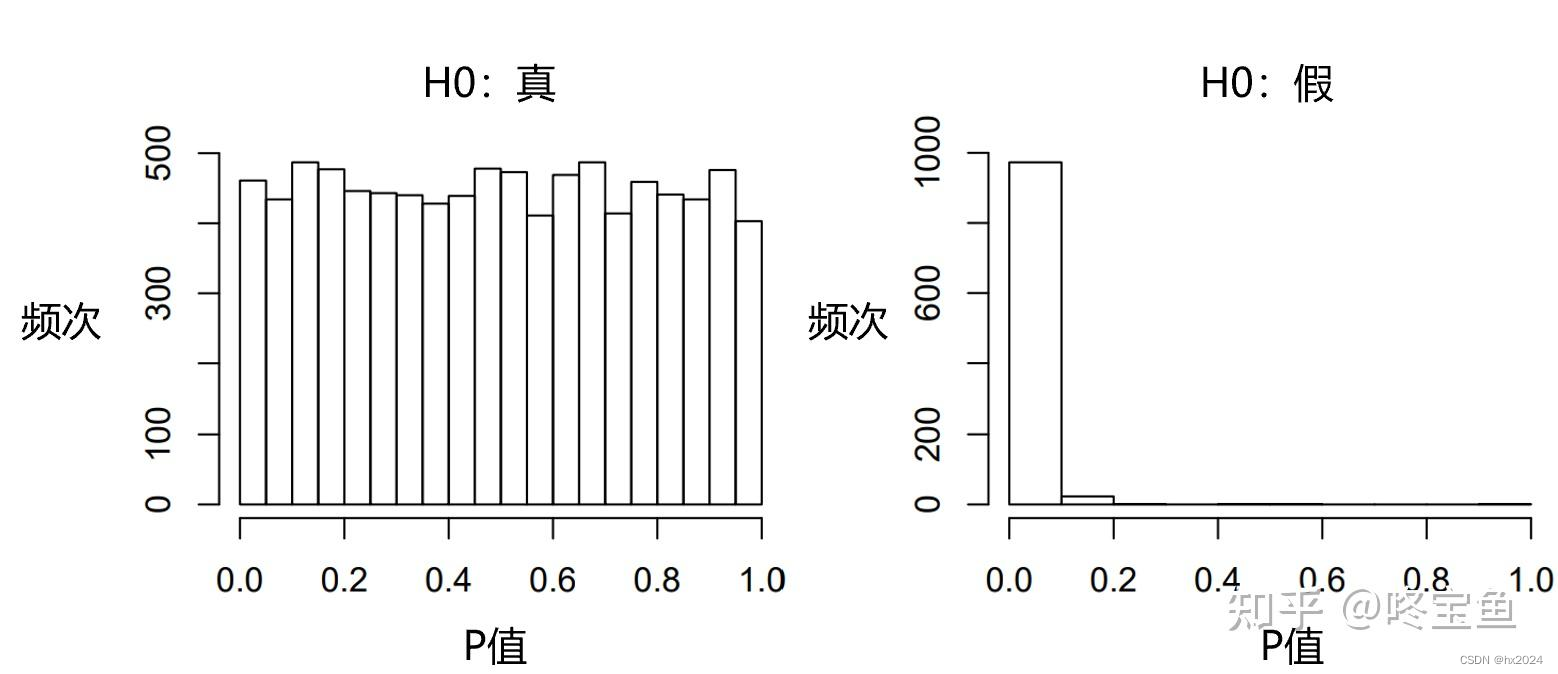
H0为真时，P值均匀分布在0%-100%之间，为什么会是均匀分布呢？是因为在零假设H0条件下，P值有5%的可能性小于5%，有10%的可能性小于10%，有20%的可能性小于20%，以此类推，可以很直观理解P值的均匀分布。而上图之所以不是完全的均匀分布，是因为样本数量还不够大（当样本数量越大，P值也就越接近于均匀分布）。

H0为假时，P值就不再是均匀分布了，而是集中在0%附近，其他区间基本没有出现。这也比较好理解：H0是假，假设检验的功效越大，检验出H0为假的能力就越好，也就意味着P值越小，拒绝H0的证据越明显。

彻底理解Benjamini-Hochberg方法原理 - 知乎 (zhihu.com)

校正P值比较：?p.adjust函数

?p.adjust
p.adjust(p, method = p.adjust.methods, n = length(p))

p.adjust.methods
# c("holm", "hochberg", "hommel", "bonferroni", "BH", "BY",
#   "fdr", "none")

##示例：
set.seed(123)
#前25个元素的均值为0，后25个元素的均值为3
x <- rnorm(50, mean = c(rep(0, 25), rep(3, 25)))
#基于向量x计算了一个对应的概率值向量p，概率值乘以2
p <- 2*pnorm(sort(-abs(x)))

round(p, 3)#保留3位小数
round(p.adjust(p), 3)
round(p.adjust(p, "BH"), 3)

Data$Bonferroni =
      p.adjust(Data$Raw.p,
               method = "bonferroni")

Data$BH =
      p.adjust(Data$Raw.p,
               method = "BH")

Data$Holm =
      p.adjust(Data$ Raw.p,
               method = "holm")

Data$Hochberg =
      p.adjust(Data$ Raw.p,
               method = "hochberg")

Data$Hommel =
      p.adjust(Data$ Raw.p,
               method = "hommel")

Data$BY =
      p.adjust(Data$ Raw.p,
               method = "BY")

Data

详见：R语言多重比较示例：Bonferroni校正法和Benjamini & Hochberg法-腾讯云开发者社区-腾讯云 (tencent.com)