陷波器滤波参数推导

1. 定义技术指标

• 采样频率 fs = 20KHz
• 中心频率 fc = 100Hz
• 陷波宽度 band(B) = 20Hz
• 陷波深度 depth = 40db

2. 计算参数

陷波器的标准传递函数为：
$$H(s)=\frac{s^2+2{\xi }_1{\omega }_c+{\omega }_c^2}{s^2+2{\xi }_2{\omega }_c+{\omega }_c^2}\text{\hspace{1em}(1)}$$
其中${\omega }_c$为陷波频率，${\xi }_1,{\xi }_2$为陷波系数.
用双线性变换法离散化(1)式可得（参考<常见三种陷波滤波器（Notch Filter）的离散化设计>）：
$$Y(z)=\frac{n_0+n_1{z}^{?1}+n_2{z}^{?2}}{d_0+d_1{z}^{?1}+d_2{z}^{?2}}$$
其中：
$$n_0={\omega }_c^2{T}_s^2+4T_s{\xi }_2{\omega }_c+4$$
$$n_1=2{\omega }_c^2{T}_s^2?8$$
$$n_2={\omega }_c^2{T}_s^2?4T_s{\xi }_2{\omega }_c+4$$

$$d_0={\omega }_c^2{T}_s^2+4T_s{\xi }_1{\omega }_c+4$$
$$d_1=2{\omega }_c^2{T}_s^2?8$$
$$d_2={\omega }_c^2{T}_s^2?4T_s{\xi }_1{\omega }_c+4$$

为了补偿离散化带来的频率畸变，将系数中的${\omega }_c$用$\frac{2}{T_s}\tan {\omega }_c{T}_s/2$替代，并简化，可得($d,n$同除了4)：
$$n_0={\tan }^2(\frac{\pi f_c}{f_s})+2{\xi }_2\tan (\frac{\pi f_c}{f_s})+1$$
$$n_1=2{\tan }^2(\frac{\pi f_c}{f_s})?2$$
$$n_2={\tan }^2(\frac{\pi f_c}{f_s})?2{\xi }_2\tan (\frac{\pi f_c}{f_s})+1$$

$$d_0={\tan }^2(\frac{\pi f_c}{f_s})+2{\xi }_1\tan (\frac{\pi f_c}{f_s})+1$$
$$d_1=2{\tan }^2(\frac{\pi f_c}{f_s})?2$$
$$d_2={\tan }^2(\frac{\pi f_c}{f_s})?2{\xi }_1\tan (\frac{\pi f_c}{f_s})+1$$

根据参考文献参考<常见三种陷波滤波器（Notch Filter）的离散化设计>的推导，${\xi }_1,{\xi }_2$与陷波器参数之间存在如下关系：

$${\xi }_1=\sqrt{\frac{\sqrt{\frac{4{\pi }^2{B}^2}{{\omega }_c^2}+1}+1}{?4dept{h}^2+2}}\text{\hspace{1em}(2)}$$

$${\xi }_2=depth?{\xi }_1$$

观察${\xi }_1$的表达式，可以发现：

• 一般滤波深度比较小，比如0.01(40db),平方之后近似为零，因此分母近似为2
• 分母的变量部分约等于滤波宽度与中心频率的比值，因此当中心频率远大于滤波宽度时（比如10倍），分子也近似等于2，
  因此，在满足上述两个条件时，则整个${\xi }_1$的值，非常接近于1，如下图所示（x为中心角频率，y为${\xi }_1$)：

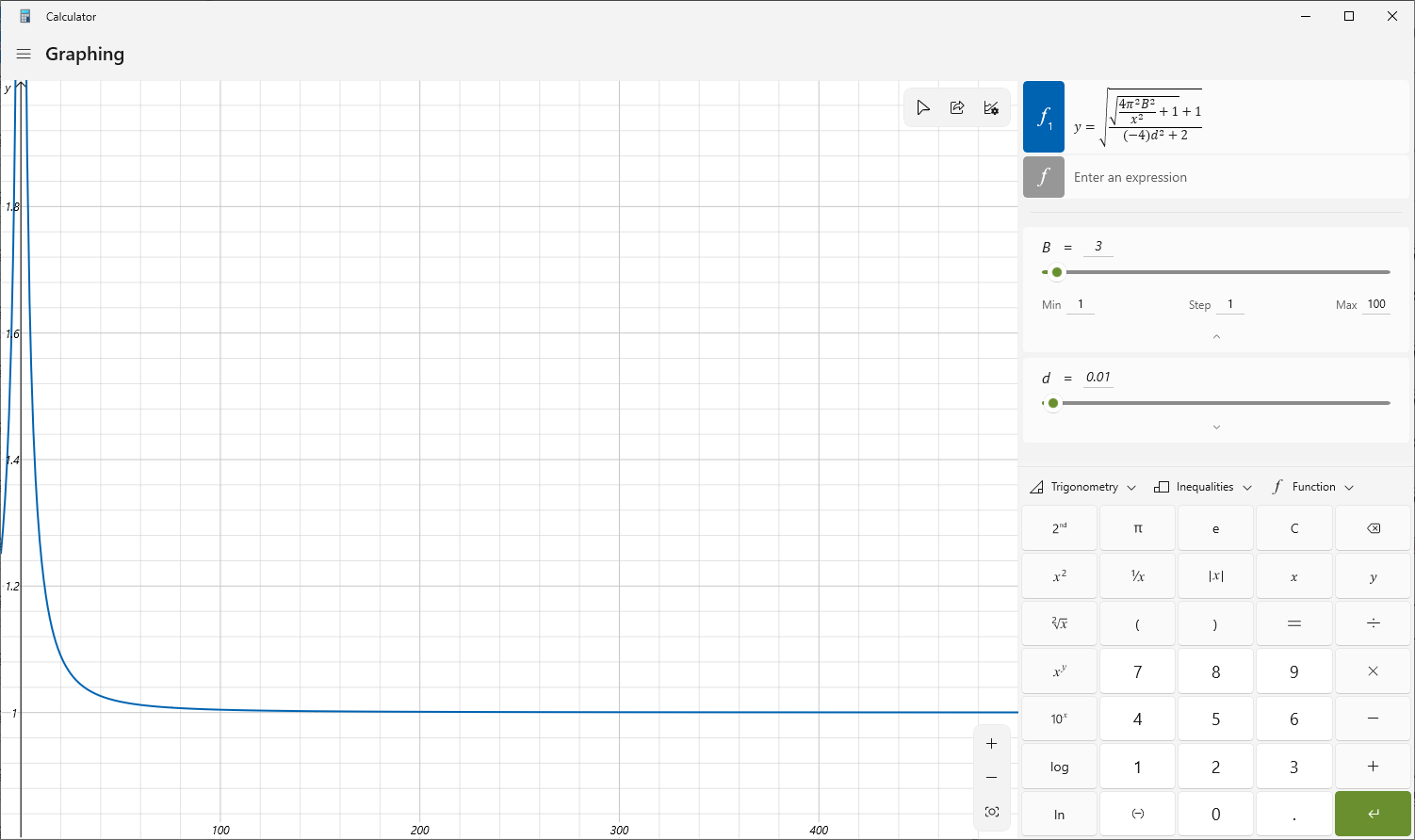
因此为简单起见，或者在嵌入式系统中为减少计算量，可以将${\xi }_1$固定为1