【LeetCode】数组精选17题——双指针、滑动窗口、前缀和

目录

快慢指针：

1. 移动零（简单）

2. 复写零（简单）

对撞指针：

1. 两数之和 II - 输入有序数组（中等）

2. 三数之和（中等）

3. 有效三角形的个数（中等）

4. 四数之和（中等）

5. 盛最多水的容器（中等）

滑动窗口：

1. 长度最小的子数组（中等）

2.?将 x 减到 0 的最小操作数（中等）

3.?乘积小于 K 的子数组（中等）

4. 最大连续1的个数 III（中等）

5. 水果成篮（中等）

前缀和：

1. 寻找数组的中心下标（简单）

2. 和为 K 的子数组（中等）

3. 连续数组（中等）

4. 二维区域和检索 - 矩阵不可变（中等）

5. 矩阵区域和（中等）

---

双指针是一种常用的算法技巧，通常用于线性数据结构（数组、字符串、链表），使用两个指针扫描。指针并不是指C语言中的指针，而是指能定位数据结构中某个数据的手段，在数组中指的是下标。

双指针的形式：

• 快慢指针：两个指针从一端向另一端移动，但移动速度不同
• 对撞指针：两个指针从两端向中间移动，直到相遇或错开

滑动窗口是一种特殊的双指针，两个指针构造一个窗口，用于解决子数组的问题。右边界右移为进窗口，左边界右移为出窗口。

正数数组中子数组的和或积，就可以用滑动窗口解决。如果数组元素不全为正数，求子数组的和不能用滑动窗口，因为当数组中有负数时在子数组中添加数字不一定能增加数组之和，从子数组中删除数字也不一定能减少子数组之和。这时就需要用到前缀和思想。

快慢指针：

1. 移动零（简单）

数组分块问题，即根据一种划分方式，将数组分成两块，可以使用双指针解决。

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int n = nums.size();
        int slow = -1; // 指向非0元素的最后一个
        int fast = 0;  // 指向待处理元素的第一个

        while (fast < n)
        {
            if (nums[fast] == 0) // fast扫描到0
            {
                fast++;
            }
            else // fast扫描到非0
            {
                swap(nums[++slow], nums[fast]);
                fast++;
            }
        }
    }
};

2. 复写零（简单）

如果从前往后原地复写0的话，会导致后面的元素被覆盖。例如，[2,0,5,1]? ? ->? ? [2,0,0,1]

所以本题采用从后往前复写0，首先要找到原数组从哪里截断。

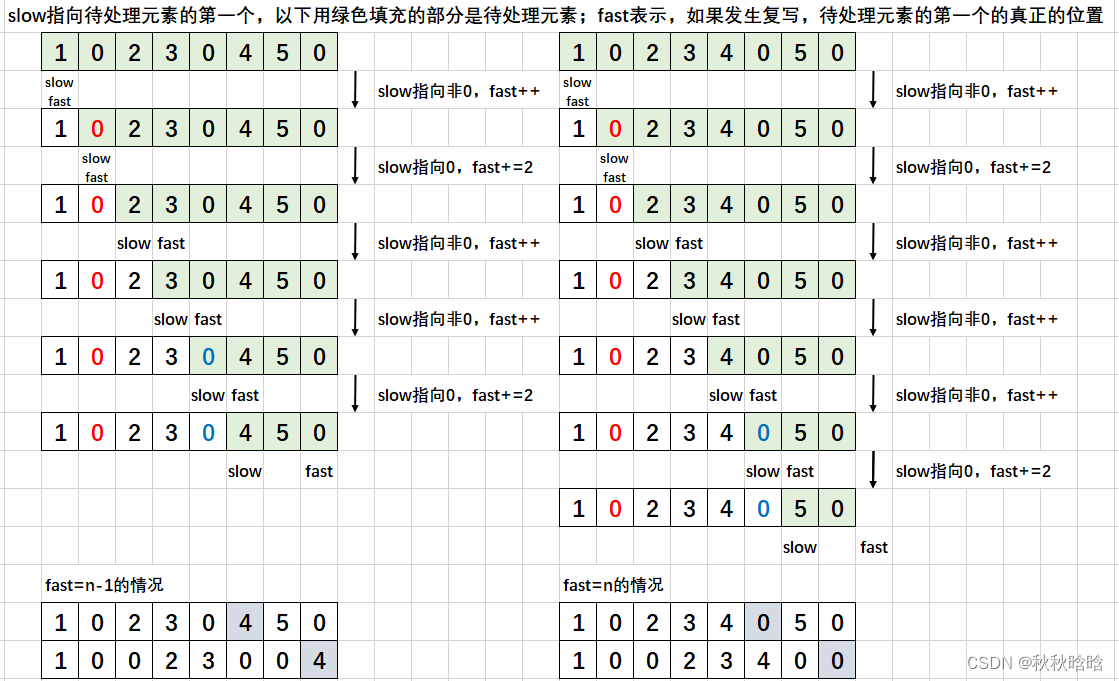
当fast = n - 1时，说明数组给待处理元素剩的位置只有1个了，这个位置就是留给slow的，不管arr[slow]是0还是非0。将arr[slow]填到数组最后一个位置，然后从slow - 1开始从后往前复写。

当fast = n时，说明数组给待处理元素已经不剩位置了，并且fast一定是从n - 2位置走两步到n，所以上一步的slow一定指向0，然后写了2个0，到达数组末尾。将0填到数组最后一个和倒数第二个位置，然后从slow-2开始从后往前复写。

class Solution {
public:
    void duplicateZeros(vector<int>& arr) {
        int n = arr.size();
        int slow = 0;
        int fast = 0;
        // 找到截断点
        while (fast < n - 1)
        {
            // slow指向待处理元素的第一个
            // fast表示，如果发生复写，待处理元素的第一个的真正的位置
            if (arr[slow])
            {
                fast++;
            }
            else
            {
                fast +=2;
            }
            slow++;
        }
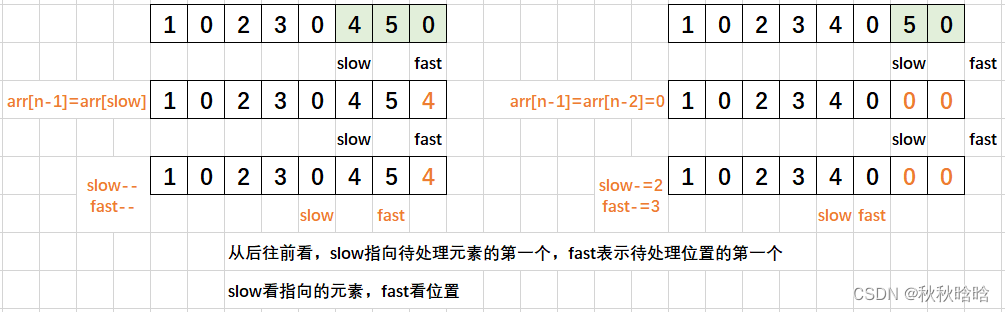
        // 判断fast，然后让slow指向待处理元素的第一个，fast表示待处理位置的第一个
        if (fast == n - 1)
        {
            arr[n - 1] = arr[slow];
            slow--;
            fast--;
        }
        else
        {
            arr[n - 1] = arr[n - 2] = 0;
            slow -= 2;
            fast -= 3;
        }
        // 从后往前复写
        while (slow >= 0)
        {
            if (arr[slow])
            {
                arr[fast] = arr[slow];
                fast--;
            }
            else
            {
                arr[fast] = arr[fast - 1] = 0;
                fast -= 2;
            }
            slow--;
        }
    }
};

对撞指针：

1. 两数之和 II - 输入有序数组（中等）

对撞指针的应用之一就是求排序数组的两个数字之和。如果和 < 目标值，左指针++，如果和 > 目标值，右指针--，直到和 == 目标值，就找到了那两个数。

class Solution {
public:
    vector<int> twoSum(vector<int>& numbers, int target) {
        int n = numbers.size();
        int left = 0;
        int right = n - 1;
        while (left < right)
        {
            if (numbers[left] + numbers[right] < target)
            {
                left++;
            }
            else if (numbers[left] + numbers[right] > target)
            {
                right--;
            }
            else
            {
                return { ++left,++right }; // 因为下标从1开始
            }
        }
        return { -1,-1 };
    }
};

2. 三数之和（中等）

和两数之和类似，如果是排序数组，那么固定nums[i]，用对撞指针从i的后面找nums[left] + nums[right] == -nums[i]。

答案不能有重复，所以要在找到一种答案后，跳过重复的元素。

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        int n = nums.size();
        sort(nums.begin(), nums.end());
        vector<vector<int>> ans;
        
        for (int i = 0; i < n - 2; )
        {
            int left = i + 1;
            int right = n - 1;
            while (left < right)
            {
                if (nums[left] + nums[right] < -nums[i])
                {
                    left++;
                }
                else if (nums[left] + nums[right] > -nums[i])
                {
                    right--;
                }
                else
                {
                    ans.push_back({ nums[i],nums[left++],nums[right--] });
                    // 去重left
                    while (left < right && nums[left] == nums[left - 1])
                    {
                        left++;
                    }
                    // 去重right
                    while (left < right && nums[right] == nums[right + 1])
                    {
                        right--;
                    }
                }
            }
            i++;
            // 去重i
            while (i < n - 2 && nums[i] == nums[i - 1])
            {
                i++;
            }
        }
        return ans;
    }
};

3. 有效三角形的个数（中等）

三角形的判定：任意两边之和大于第三边。

只要两条较短边>最长边，就可以推出任意两边之和大于第三边。

和三数之和类似，先给数组排序，固定最长边nums[i]，用对撞指针从i的前面找nums[left] + nums[right] > nums[i]。

一旦向右移动left到某个位置时nums[left] + nums[right] > nums[i]，就不需要再向右移动left了。因为只要保持right不动，[left, right)这个下标区间对应的任意一个元素，加上nums[right]，都一定比nums[i]大。此时两个指针之间有多少个数字，就找到了多少组两条较短边>最长边。

答案可以有重复，不用跳过重复的元素。

class Solution {
public:
    int triangleNumber(vector<int>& nums) {
        int n = nums.size();
        sort(nums.begin(), nums.end());
        int ans = 0;

        for (int i = n - 1; i >= 2; i--)
        {
            int left = 0;
            int right = i - 1;
            while (left < right)
            {
                if (nums[left] + nums[right] > nums[i])
                {
                    ans += right - left;
                    right--;
                }
                else
                {
                    left++;
                }
            }
        }
        return ans;
    }
};

4. 四数之和（中等）

先排序，固定一个数nums[a]，再利用三数之和的解法找到三个数nums[b] nums[c] nums[d]，使

nums[b] + nums[c] + nums[d] == target - nums[a]。

答案不能有重复，所以要在找到一种答案后，跳过重复的元素。

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        int n = nums.size();
        sort(nums.begin(), nums.end());
        vector<vector<int>> ans;
        
        for (int i = 0; i < n - 3; ) // 固定nums[i]
        {
            for (int j = i + 1; j < n - 2; ) // 固定nums[j]
            {
                int sum1 = nums[i] + nums[j];
                int left = j + 1;
                int right = n - 1;
                while (left < right)
                {
                    int sum2 = nums[left] + nums[right];
                    if (sum2 < (long long)target - sum1)
                    {
                        left++;
                    }
                    else if (sum2 > (long long)target - sum1)
                    {
                        right--;
                    }
                    else
                    {
                        ans.push_back({ nums[i],nums[j],nums[left++],nums[right--] });
                        // 去重left
                        while (left < right && nums[left] == nums[left - 1])
                        {
                            left++;
                        }
                        // 去重right
                        while (left < right && nums[right] == nums[right + 1])
                        {
                            right--;
                        }
                    }
                }
                j++;
                // 去重j
                while (j < n - 2 && nums[j] == nums[j - 1])
                {
                    j++;
                }
            }
            i++;
            // 去重i
            while (i < n - 3 && nums[i] == nums[i - 1])
            {
                i++;
            }
        }
        return ans;
    }
};

5. 盛最多水的容器（中等）

假设左板的下标是left，右板的下标是right，两板与x轴构成的矩形的面积为：

S = (right - left) * min(height[left], height[right])

显然，矩形的面积由底边宽度和短板长度共同决定。

如果改变短板，向内收窄一格，底边宽度-1，短板的长度可能会变大，矩形的面积可能变大。

如果改变长板，向内收窄一格，底边宽度-1，由于短板决定高度，长板再怎么改变也没有用，矩形的面积一定变小。

class Solution {
public:
    int maxArea(vector<int>& height) {
        int n = height.size();
        int left = 0;
        int right = n - 1;
        int ans = 0;
        while (left < right)
        {
            ans = max(ans, ((right - left) * min(height[left], height[right])));
            if (height[left] < height[right])
            {
                left++;
            }
            else
            {
                right--;
            }
        }
        return ans;
    }
};

滑动窗口：

1. 长度最小的子数组（中等）

进窗口后判断子数组的和是否>= target，如果找到了和>= target的子数组，更新结果，然后出窗口，缩小子数组的长度，直到子数组的和 < target。

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int n = nums.size();
        int left = 0;
        int right = 0;
        int sum = 0;
        int ans = INT_MAX;
        while (right < n)
        {
            // 进窗口
            sum += nums[right];
            // 判断子数组的和是否>=target
            while (sum >= target && left <= right)
            {
                // 更新结果
                ans = min(ans, right - left + 1);
                // 出窗口
                sum -= nums[left++];
            }
            // 更新右边界
            right++;
        }
        return ans == INT_MAX ? 0 : ans;
    }
};

2.?将 x 减到 0 的最小操作数（中等）

问题可以理解成：求和为x的最左端子数组和最右端子数组的最小长度。

把问题转化成：求和为total - x的子数组的最大长度（total为数组所有元素的和）。

这道题nums[i]的取值范围是：1 <= nums[i] <= 104，求正数数组中子数组的和，显然用滑动窗口。

进窗口后判断子数组的和是否> total - x，如果已经> total - x了，要出窗口，减小子数组的和，直<= total - x。然后判断子数组的和到底是不是==?total - x，如果找到了和==?total - x的子数组，更新结果。

class Solution {
public:
    int minOperations(vector<int>& nums, int x) {
        int n = nums.size();
        int total = 0;
        for (auto& e : nums)
        {
            total += e;
        }

        int left = 0;
        int right = 0;
        int sum = 0;
        int ans = -1;
        while (right < n)
        {
            // 进窗口
            sum += nums[right];
            // 判断子数组的和是否>total-x
            while (sum > total - x && left <= right)
            {
                // 出窗口
                sum -= nums[left++];
            }
            // 找到和为total-x的子数组，更新结果
            if (sum == total - x)
            {
                ans = max(ans, right - left + 1);
            }
            // 更新右边界
            right++;
        }
        return ans == -1 ? ans : n - ans;
    }
};

3.?乘积小于 K 的子数组（中等）

进窗口后判断子数组的积是否>= k，如果已经 >= k了，要出窗口，减小子数组的积，直到< k。这时得到的子数组就是满足条件的子数组，并且，只要保持右边界不动，向右移动左边界形成的所有子数组的积就一定< k。此时左右边界之间有多少个元素，就找到了多少个乘积< k的子数组。

class Solution {
public:
    int numSubarrayProductLessThanK(vector<int>& nums, int k) {
        int n = nums.size();
        int left = 0;
        int right = 0;
        int prod = 1;
        int ans = 0;
        while (right < n)
        {
            // 进窗口
            prod *= nums[right];
            // 判断子数组的积是否>=k
            while (prod >= k && left <= right)
            {
                // 出窗口
                prod /= nums[left++];
            }
            // 更新结果
            ans +=  right - left + 1;
            // 更新右边界
            right++;
        }
        return ans;
    }
};

4. 最大连续1的个数 III（中等）

把问题转化成：求0的个数不超过k个的最长子数组。

用zero记录窗口中0的个数。进窗口的同时要维护zero，然后判断zero是否> k，如果已经> k了，要出窗口并维护zero，直到<= k。这时就找到了0的个数不超过k个的子数组，更新结果。

class Solution {
public:
    int longestOnes(vector<int>& nums, int k) {
        int n = nums.size();
        int left = 0;
        int right = 0;
        int zero = 0; // 窗口中0的个数
        int ans = 0;
        while (right < n)
        {
            // 进窗口+维护zero
            if (nums[right] == 0)
                zero++;
            // 判断zero是否>k
            while (zero > k && left <= right)
            {
                // 出窗口+维护zero
                if (nums[left] == 0)
                {
                    zero--;
                }
                left++;
            }
            // 更新结果
            ans = max(ans, right - left + 1);
            // 更新右边界
            right++;
        }
        return ans;
    }
};

5. 水果成篮（中等）

把问题转化成：求元素的种类只有2种的最长子数组。

用哈希表记录窗口中元素的种类和次数，key——元素的种类，value——每个元素出现的次数，哈希表的大小表示有多少种元素在窗口中。

进窗口后判断哈希表的大小是否> 2，如果已经> 2了，要出窗口，记得要把value为0的键值对删除，直到哈希表的大小== 2。这时就找到了元素的种类只有2种的子数组，更新结果。

class Solution {
public:
    int totalFruit(vector<int>& fruits) {
        int n = fruits.size();
        int left = 0;
        int right = 0;
        unordered_map<int, int> hash; // key——元素的种类，value——每个元素出现的次数
        int ans = 0;
        while (right < n)
        {
            // 进窗口
            hash[fruits[right]]++;
            // 判断哈希表的大小是否>2
            while (hash.size() > 2 && left <= right)
            {
                // 出窗口
                hash[fruits[left]]--;
                if (hash[fruits[left]] == 0)
                {
                    hash.erase(fruits[left]);
                }
                left++;
            }
            // 更新结果
            ans = max(ans, right - left + 1);
            // 更新右边界
            right++;
        }
        return ans;
    }
};

前缀和：

1. 寻找数组的中心下标（简单）

如果sum - nums[i] == total - sum，i就是中心下标。

class Solution {
public:
    int pivotIndex(vector<int>& nums) {
        int n = nums.size();
        int total = 0; // 所有元素的和
        for (auto& i : nums)
        {
            total += i;
        }
        int sum = 0; // 表示左子数组的和+nums[i]
        for (int i = 0; i < n; i++)
        {
            sum += nums[i];
            if (sum - nums[i] == total - sum)
                return i;
        }
        return -1;
    }
};

2. 和为 K 的子数组（中等）

每次累加新的前缀和，都往前找找有没有以前的前缀和 == 新的前缀和 - k。

用哈希表记录前缀和出现的次数，默认添加一个键值对(0, 1)。用sum表示当前位置的前缀和。

例如，nums = [3,2,1]，k = 3，

将nums[0]添加进sum，sum = 3，sum - k = 0，恰好哈希表中存放了值为0的前缀和，出现的次数为1，将出现的次数添加进ans中，ans = 1。然后把当前位置的前缀和在哈希表中对应的值++，此时哈希表中有2个键值对：(0, 1), (3, 1)。

将nums[1]添加进sum，sum = 5，sum - k = 2，哈希表中没有存放值为2的前缀和，没找到满足条件的子数组，对ans不做处理。然后把当前位置的前缀和在哈希表中对应的值++，此时哈希表中有3个键值对：(0, 1), (3, 1), (5, 1)。

将nums[2]添加进sum，sum = 6，sum - k = 3，恰好哈希表中存放了值为3的前缀和，出现的次数为1，将出现的次数添加进ans中，ans = 2。然后把当前位置的前缀和在哈希表中对应的值++，此时哈希表中有4个键值对：(0, 1), (3, 1), (5, 1), (6, 1)。

循环结束，输出ans。

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {      
        int n = nums.size();
        unordered_map<int, int> hash; // key——前缀和 value——出现的次数
        hash[0] = 1; // 添加(0, 1)
        int sum = 0; // 当前位置的前缀和
        int ans = 0;
        for (auto& i : nums)
        {
            sum += i;
            if (hash.count(sum - k))
            {
                ans += hash[sum - k];
            }
            hash[sum]++;
        }
        return ans;
    }
};

3. 连续数组（中等）

把数组所有0替换成-1，题目转变为：找到和为0的最长连续子数组。

每次累加新的前缀和，都往前找找有没有以前的前缀和 == 新的前缀和。

用哈希表记录前缀和对应的最小下标（因为求最大子数组），默认添加一个键值对(0, -1)。用sum表示当前位置的前缀和。

例如，nums = [0,1,0]，

将nums[0]添加进sum，如果是0，添加-1，如果是1，添加1，sum = -1，哈希表中没有存放值为-1的前缀和，没找到满足条件的子数组，对ans不做处理。然后把当前位置的前缀和及下标添加进哈希表中，此时哈希表中有2个键值对：(0, -1), (-1, 0)。

将nums[1]添加进sum，如果是0，添加-1，如果是1，添加1，sum = 0，恰好哈希表中存放了值为0的前缀和，下标为-1，所以子数组长度为1 - (-1) = 2，将它和ans比较，取最大的，ans = 2。

将nums[2]添加进sum，如果是0，添加-1，如果是1，添加1，sum = -1，恰好哈希表中存放了值为-1的前缀和，下标为0，所以子数组长度为2 - 0 = 2，将它和ans比较，取最大的，ans = 2。

循环结束，输出ans。

class Solution {
public:
    int findMaxLength(vector<int>& nums) {
        int n = nums.size();
        unordered_map<int, int> hash; // key——前缀和 value——最小下标
        hash[0] = -1; // 添加(0, -1)
        int sum = 0; // 当前位置的前缀和
        int ans = 0;
        for (int i = 0; i < n; i++)
        {
            sum += nums[i] == 0 ? -1 : 1;
            if (hash.count(sum))
            {
                ans = max(ans, i - hash[sum]);
            }
            else
            {
                hash[sum] = i;
            }
        }
        return ans;
    }
};

4. 二维区域和检索 - 矩阵不可变（中等）

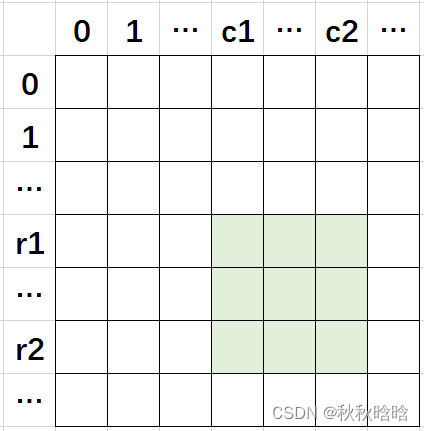
创建一个和matrix一样大的二维前缀和数组sums，sums[i][j]记录matrix从(0,0)到(i,j)的子矩阵数字和。

(r1,c1)->(r2,c2)子矩阵数字和 =

sums[r2][c2] - sums[r2][c1 - 1] - sums[r1 - 1][c2] + sums[r1 - 1][c1 - 1]

如果r1或c1为0，r1 - 1或c1 - 1会越界。

为了防止越界，在sums的上面和左面分别加一行0和一列0，这样的话，sums[i+1][j+1]记录matrix从(0,0)到(i,j)的子矩阵数字和。

所以，(r1,c1)->(r2,c2)子矩阵数字和 =

sums[r2 + 1][c2 + 1] - sums[r2 + 1][c1] - sums[r1][c2 + 1] + sums[r1][c1]

class NumMatrix {
public:
    public:
    NumMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        sums.resize(m + 1, vector<int>(n + 1, 0)); // 上面和左面分别加一行0和一列0，防止越界
        // 处理前缀和数组
        for (int i = 0; i < m; i++)
        {
            int rowSum = 0;
            for (int j = 0; j < n; j++)
            {
                rowSum += matrix[i][j];
                sums[i + 1][j + 1] = sums[i][j + 1] + rowSum;
            }
        }
    }
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        return sums[row2 + 1][col2 + 1] - sums[row2 + 1][col1] - sums[row1][col2 + 1] + sums[row1][col1];
    }

private:
    vector<vector<int>> sums; // sums[i+1][j+1]记录matrix从(0,0)到(i,j)的子矩阵数字和
};

5. 矩阵区域和（中等）

和上一题“二维矩阵区域和检索 - 矩阵不可变”类似。

注意矩阵左上角和右下角坐标的确定：

• 左上角：r1 = max(0, i - k)? ? ? ? ? c1 = max(0, j - k)
• 右下角：r2 = min(m - 1, i + k)? ? c2 = min(n - 1, j + k)

class Solution {
public:
    vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
        int m = mat.size();
        int n = mat[0].size();

        // 处理前缀和矩阵
        vector<vector<int>> sums(m + 1, vector<int>(n + 1, 0)); // sums[i+1][j+1]记录matrix从(0,0)到(i,j)的子矩阵数字和
        for (int i = 0; i < m; i++)
        {
            int rowSum = 0;
            for (int j = 0; j < n; j++)
            {
                rowSum += mat[i][j];
                sums[i + 1][j + 1] = sums[i][j + 1] + rowSum;
            }
        }

        // 处理ans矩阵
        vector<vector<int>> ans(m, vector<int>(n));
        for (int i = 0; i < m; i++)
        {
            for (int j = 0; j < n; j++)
            {
                int r1 = max(0, i - k);
                int c1 = max(0, j - k);
                int r2 = min(m - 1, i + k);
                int c2 = min(n - 1, j + k);
                ans[i][j] = sums[r2 + 1][c2 + 1] - sums[r2 + 1][c1] - sums[r1][c2 + 1] + sums[r1][c1];
            }
        }
        return ans;
    }
};