【教学类-43-12】 20240102 3-9宫格数独有多少不重复的基础模板(3宫格12套,4宫格288套……)
发布时间:2024年01月02日
作品展示:
背景需求:
用以上这套代码打印A4纸的宫格题
根据实际需求,打印了3宫格5张、5宫格5张、9宫格2张



看着3宫格的打印纸,我突然想“2宫格数独只有 2种排列”方法,那么“3宫格”会有几种不重复的排列方法

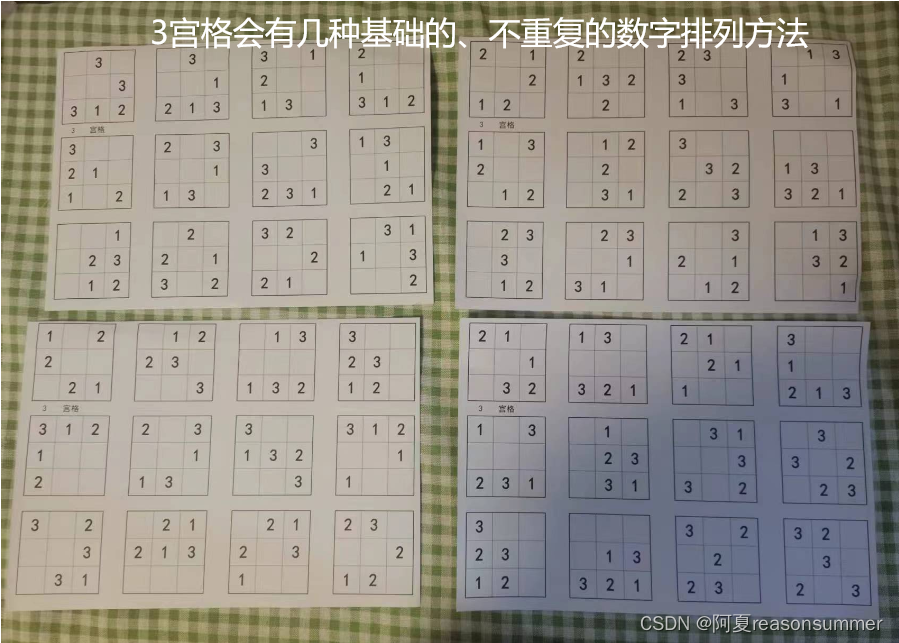
(不考虑空缺,只要最基本的不重复数字排列模板)
代码展示:
运用1.0数独代码修改后获得,因为是随机生成,可能会有大量重复,因此需要尽量生成最大次数,从中进行排重。获得X宫格最多的不重复套数。
这种测试非常耗时!!!
第一次3-9宫格生成次数是百万次(1000,000),耗时1小时。
'''
目的:数独11 N宫格有几种不重复的排列基础模板,3宫格有12种,4宫格有576种
作者:阿夏(参考)
时间:2024年1月2日 13:35
'''
import random
from win32com.client import constants,gencache
from win32com.client.gencache import EnsureDispatch
from win32com.client import constants # 导入枚举常数模块
import os,time
import docx
from docx import Document
from docx.shared import Pt
from docx.shared import RGBColor
from docx.enum.text import WD_PARAGRAPH_ALIGNMENT
from docx.oxml.ns import qn
from docxtpl import DocxTemplate
import pandas as pd
from docx2pdf import convert
from docx.shared import RGBColor
# 生成题库
import random
import copy
# num=int(input('生成几份\n'))
# 制作"单元格"# 几宫格
# hsall=int(input('请输入3-9\n'))
t=1000000
# int(input('生成条数100000条\n'))
# hsal=hsall
# kk=int(input('空格数量,输入5,就是50%,就是空一半)\n'))
P=[]
Q=[]
R=[]
for hs in [3,4,5,6,7,8,9]:
for k in range(t):
# 测试十万条
P.clear()
# Q.clear()
# ————————————————生成随机宫格,按比例空缺格子
# 版权声明:本文为CSDN博主「Vaeeeeeee」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
# 原文链接:https://blog.csdn.net/m0_46366547/article/details/131334720
def generate_sudoku_board():
# 函数体生成数独库表盘
# 创建一个9x9的二维列表,表示数独棋盘
board = [[0] * hs for _ in range(hs)]
# 递归函数,用于填充数独棋盘的每个单元格
def filling_board(row, col):
# 检查是否填充完成整个数独棋盘
if row == hs:
return True
# 计算下一个单元格的行和列索引
next_row = row if col < hs-1 else row + 1
next_col = (col + 1) % hs
# 获取当前单元格在小九宫格中的索引
box_row = row
box_col = col
# 随机生成1到9的数字
numbers = random.sample(range(1, hs+1), hs)
for num in numbers:
# 检查行、列、小九宫格是否已经存在相同的数字
if num not in board[row] and all(board[i][col] != num for i in range(hs)) and all(num != board[i][j] for i in range(box_row, box_row) for j in range(box_col, box_col)):
board[row][col] = num
# 递归填充下一个单元格
if filling_board(next_row, next_col):
return True
# 回溯,将当前单元格重置为0
board[row][col] = 0
return False
# 填充数独棋盘
filling_board(0, 0)
return board
def create_board(): # level数字越大代表游戏难度越大
"""
生成一个随机的数独棋盘,不要空白
"""
board = generate_sudoku_board()
board1 = copy.deepcopy(board)
blanks = random.sample(range(hs*hs), 0)
for i in blanks:
row = i // hs
col = i % hs
board[row][col] = 0
# if random.randint(0, hs) < level:
# board1[row][col] = 0
return board
v = create_board()
# v = board()
# 81空34、46
# # 提取每个元素
for a1 in v: # 第一次读取,[a,b][c,d][e,f]的内容-列表
for a2 in a1: # 第二次读取,[a,b,c,d,e,f]的内容-元素
if a2==0: # 如果某个元素==0,就替换成空
P.append('')
else: # 如果某个元素非0,就写入本身的数字
P.append(a2)
# print(P)
# [2, 1, 3, 1, 3, 2, 3, 2, 1]
# 把N次的结果组合成列表
for p in P:
Q.append(p)
# print(Q)
# print(len(Q))
# [1, 3, 2, 2, 1, 3, 3, 2, 1, 1, 2, 3, 3, 1, 2, 2, 3, 1, 2, 1, 3, 1, 3, 2, 3, 2, 1]
# 3*3拆分9条9条一组
for k in range(int(len(Q)/(hs*hs))):
R.append(Q[hs*hs*k:hs*hs*k+hs*hs])
# print(R)
# 要排除重复的数组,你可以使用集合(Set)来存储每个排列,因为集合会自动去重。你可以遍历数组,将每个数组转换为元组,然后将元组添加到集合中。最后,将集合转换回列表形式即可。
unique_array = list(set(tuple(row) for row in R))
unique_array = [list(row) for row in unique_array]
# print(unique_array)
print('---{} 宫格 {} 百万条生成 {} 条-----'.format(hs,t,len(unique_array)))
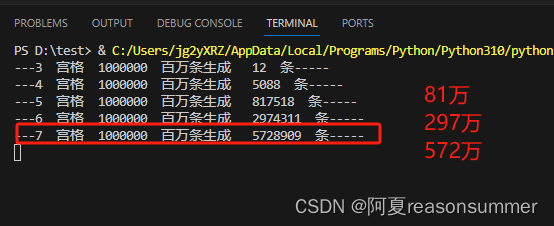
等了一个小时,4宫格有5千条,5宫格就有81万条,6宫格297万条,7宫格572万套,这种几何倍数增长的题目,显然8宫格、9宫格运行的次数需要亿万计算。生成时间更加长久,7宫格一个就需要1小时
于是我终止程序了。

把一百万次数改成5000000(五百万次)测试9宫格最大数量(如果9宫格五百万次的生成数量与四百万相同,就以五百万为基准,去测试5-8宫格的最大数量)
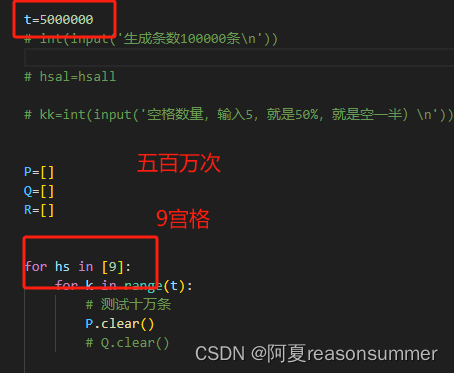
预估一个9宫格 5百万次,就要1个小时。
结果跑了 3个小时,18:35-21:36
结果不重复的答案也是五百万次,Σ(⊙▽⊙"a
我感觉这个答案有问题
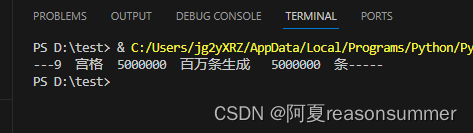
再次问了AI对话大师,它提供了数字乘阶的答案,
我试了一试阶乘的概念,


我手动画了唯一一个可以验算的3宫格,写出12套题目,发现一个规律,第一行的3个数字有2套(3-1)然后根据第一行的三个数字推算下第一列的数字也是2款(3-1)。
所以3宫格不等于3乘阶=6,这种方法不对
那么如何答案匹配。再问ChatGPT

测试3宫格的乘阶计算3!*2!*1!=12,正好等于12

测试2宫格的乘阶计算2!*1!=2,正好等于2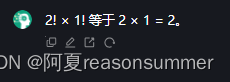
说明,乘阶计算是宫格排列数量的正确计算思路。
代码:
'''
目的:数独11 N宫格有几种不重复的排列基础模板,乘阶方法
作者:阿夏(参考)
时间:2024年1月2日 13:35
'''
import math
P=[]
Q=[]
R=[]
hsall=[]
for i in range(1,10): # 1-9宫格
hsall.append(i)
# 计算1-9各自的乘阶
jc=[]
for hs in hsall:
j = math.factorial(hs)
print('{}的阶乘是{}'.format(hs,j))
jc.append(j)
print(jc)
# [1, 2, 6, 24, 120, 720, 5040, 40320, 362880]
print(len(jc))
# jc = [1, 2, 6, 24, 120, 720, 5040, 40320, 362880]
result = []
product = 1
for num in range(len(jc)):
product *= jc[num]
print('---{} 宫格 乘阶数{} 生成 {} 条不重复模板-----'.format(hsall[num],jc[num],product))
# ---1 宫格 乘阶数1 生成 1 条不重复模板-----
# ---2 宫格 乘阶数2 生成 2 条不重复模板-----
# ---3 宫格 乘阶数6 生成 12 条不重复模板-----
# ---4 宫格 乘阶数24 生成 288 条不重复模板-----
# ---5 宫格 乘阶数120 生成 34560 条不重复模板-----
# ---6 宫格 乘阶数720 生成 24883200 条不重复模板-----
# ---7 宫格 乘阶数5040 生成 125411328000 条不重复模板-----
# ---8 宫格 乘阶数40320 生成 5056584744960000 条不重复模板-----
# ---9 宫格 乘阶数362880 生成 1834933472251084800000 条不重复模板-----
# [1, 2, 12, 288, 34560, 24883200, 125411328000, 5056584744960000, 1834933472251084800000]
# 所有答案打包
result.append(product)
print(result)
# [1, 2, 12, 288, 34560, 24883200, 125411328000, 5056584744960000, 1834933472251084800000]
乘阶计算的不重复数独样式数量
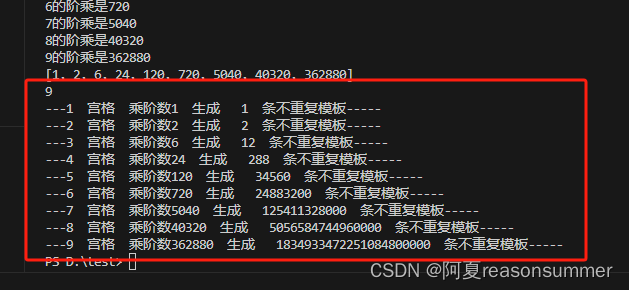

结论证明前面的“去重方法“费时又不准确。
虽然算出数量,但是具体的题目需要打印出来,验证数量是否正确,从题量看,只有3-4宫格可供验证(12、288),5-9的题量太大,无法验证
文章来源:https://blog.csdn.net/reasonsummer/article/details/135344551
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- (2023|NIPS,MUSE,掩蔽适配器,基于反馈的迭代训练)StyleDrop:任意风格的文本到图像生成
- 猫罐头哪个牌子好性价比高?五大性价比高的品牌推荐
- [React面试题]核心算法的重构----Fiber
- YOLOv8独家原创改进:多层次特征融合(SDI)结合PConv、DualConv、GSConv,实现二次创新 | UNet v2最新论文
- 手把手教你用jmeter做压力测试(详图)
- 【Python-批量修改视频分辨率】
- 【代码随想录算法训练营-第十天】【栈与队列】232.用栈实现队列,225. 用队列实现栈
- Spring高手之路-Spring事务的传播机制(行为、特性)
- 在 docker 容器中配置双网卡,解决通讯的问题
- 分享几种msvcr120.dll丢失的解决方案,以及在修复过程中的注意事项
