力扣14题-最长公共前缀[简单]
题目描述
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 ""。
示例 1:
输入:strs = ["flower","flow","flight"]
输出:"fl"示例 2:
输入:strs = ["dog","racecar","car"]
输出:""
解释:输入不存在公共前缀。提示:
- 1 <= strs.length <= 200
- 0 <= strs[i].length <= 200
- strs[i] 仅由小写英文字母组成
解法
我的解法
第一步先找出最短字符串的长度,如果存在多个长度相等的最短字符串,则找出他们之间的最长相同前缀m
最长公共前缀一定是小于等于第一步得到的这个m的
接下来,只需要对各个字符串的字符从第0位开始依次对比即可,只要出现不等的,就查找结束
时间复杂度 O(mn) 其中n是字符串数量,m是字符串平均长度
空间复杂度O(1) 使用的额外空间复杂度为常数
public String longestCommonPrefix(String[] strs) {
int minLength = strs[0].length();
String minLengthStr = strs[0];
// 第一步,查询到长度最短的字符串的长度,如果存在多个则比对其最长相同前缀的长度作为最短字符串长度
for (int i = 1; i < strs.length; i++) {
int prefixLength = 0;
if (strs[i].length() < minLength) {
minLength = strs[i].length();
} else if (strs[i].length() == minLength) {
// 若两个字符串长度相同,则查找这两个字符串的最长公共前缀长度
for (int j = 0; j < minLength; j++) {
if (minLengthStr.charAt(j) == strs[i].charAt(j)) {
prefixLength++;
} else {
break;
}
}
minLength = prefixLength;
}
}
// 所有字符串,从第0位开始依次对比该位置的字符是否相同。一旦出现不同 即查找结束
int index = 0;
while (index < minLength) {
boolean isEnd = false;
for (int i = 0; i < strs.length - 1; i++) {
if (strs[i].charAt(index) == strs[i + 1].charAt(index)) {
continue;
} else {
isEnd = true;
break;
}
}
if (isEnd) {
break;
} else {
index++;
}
}
// 查找到的最长公共前缀
String prefixStr = (index == 0) ? "" : strs[0].substring(0, index);
return prefixStr;
}官方解法
作者:力扣官方题解
链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
解法一和解法二类似。一个是 挨个字符串进行比较,另一个是 所有字符串的字符从前向后依次比较
解法三 分治 是我没有想到的
解法四 二分查找想到了,但是感觉 每次二分查找时还需要多出 logN的时间消耗 便没有选择该解法
解法一(横向扫描)
与每个字符串依次比较相同的前缀,比较一遍后 或 比较到完全不同时即结束
时间复杂度:O(mn),其中 m 是字符串数组中的字符串的平均长度,n 是字符串的数量。最坏情况下,字符串数组中的每个字符串的每个字符都会被比较一次。
空间复杂度:O(1)。使用的额外空间复杂度为常数。
public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length == 0) {
return "";
}
String prefix = strs[0];
int count = strs.length;
for (int i = 1; i < count; i++) {
prefix = longestCommonPrefix(prefix, strs[i]);
if (prefix.length() == 0) {
break;
}
}
return prefix;
}
public String longestCommonPrefix(String str1, String str2) {
int length = Math.min(str1.length(), str2.length());
int index = 0;
while (index < length && str1.charAt(index) == str2.charAt(index)) {
index++;
}
return str1.substring(0, index);
}解法二(纵向扫描)
时间复杂度:O(mn),其中 m 是字符串数组中的字符串的平均长度,n 是字符串的数量。最坏情况下,字符串数组中的每个字符串的每个字符都会被比较一次。
空间复杂度:O(1)。使用的额外空间复杂度为常数。
public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length == 0) {
return "";
}
int length = strs[0].length();
int count = strs.length;
for (int i = 0; i < length; i++) {
char c = strs[0].charAt(i);
for (int j = 1; j < count; j++) {
if (i == strs[j].length() || strs[j].charAt(i) != c) {
return strs[0].substring(0, i);
}
}
}
return strs[0];
}解法三(分治)

时间复杂度:O(mn),其中 m 是字符串数组中的字符串的平均长度,n 是字符串的数量
时间复杂度的递推式是 T(n)=2*T(n/2)+O(m),通过计算可得 T(n)=O(mn)
空间复杂度:O(mlog?n),其中 m 是字符串数组中的字符串的平均长度,n 是字符串的数量
空间复杂度主要取决于递归调用的层数,层数最大为 log?n,每层需要 m 的空间存储返回结果
public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length == 0) {
return "";
} else {
return longestCommonPrefix(strs, 0, strs.length - 1);
}
}
public String longestCommonPrefix(String[] strs, int start, int end) {
if (start == end) {
return strs[start];
} else {
int mid = (end - start) / 2 + start;
String lcpLeft = longestCommonPrefix(strs, start, mid);
String lcpRight = longestCommonPrefix(strs, mid + 1, end);
return commonPrefix(lcpLeft, lcpRight);
}
}
public String commonPrefix(String lcpLeft, String lcpRight) {
int minLength = Math.min(lcpLeft.length(), lcpRight.length());
for (int i = 0; i < minLength; i++) {
if (lcpLeft.charAt(i) != lcpRight.charAt(i)) {
return lcpLeft.substring(0, i);
}
}
return lcpLeft.substring(0, minLength);
}解法四(二分查找)
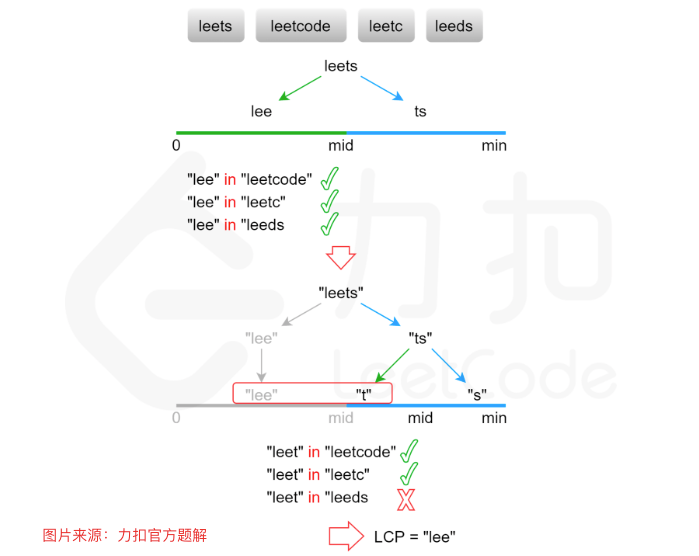
时间复杂度:O(mnlog?m),其中 m 是字符串数组中的字符串的最小长度,n 是字符串的数量。
二分查找的迭代执行次数是 O(log?m),每次迭代最多需要比较 mn 个字符,因此总时间复杂度是 O(mnlog?m)
空间复杂度:O(1)。使用的额外空间复杂度为常数
public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length == 0) {
return "";
}
int minLength = Integer.MAX_VALUE;
for (String str : strs) {
minLength = Math.min(minLength, str.length());
}
int low = 0, high = minLength;
while (low < high) {
int mid = (high - low + 1) / 2 + low;
if (isCommonPrefix(strs, mid)) {
low = mid;
} else {
high = mid - 1;
}
}
return strs[0].substring(0, low);
}
public boolean isCommonPrefix(String[] strs, int length) {
String str0 = strs[0].substring(0, length);
int count = strs.length;
for (int i = 1; i < count; i++) {
String str = strs[i];
for (int j = 0; j < length; j++) {
if (str0.charAt(j) != str.charAt(j)) {
return false;
}
}
}
return true;
}本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Neos的渗透测试靶机练习——DarkHole-2
- LaTex设置标题页、修改文字颜色和文字高亮
- 【分布式微服务专题】SpringSecurity OAuth2快速入门
- TIMESNET: TEMPORAL 2D-VARIATION MODELINGFOR GENERAL TIME SERIES ANALYSIS
- 网络流量统计
- Excel formulas 使用总结(更新中)
- ospf 知识总结
- k8s学习路线
- 【DDD分布式系统学习笔记】RPC调用以及系统初步搭建
- vue3开发一个todo List