《数据库系统原理》之关系数据库【知识点罗列+关系代数例题演练】

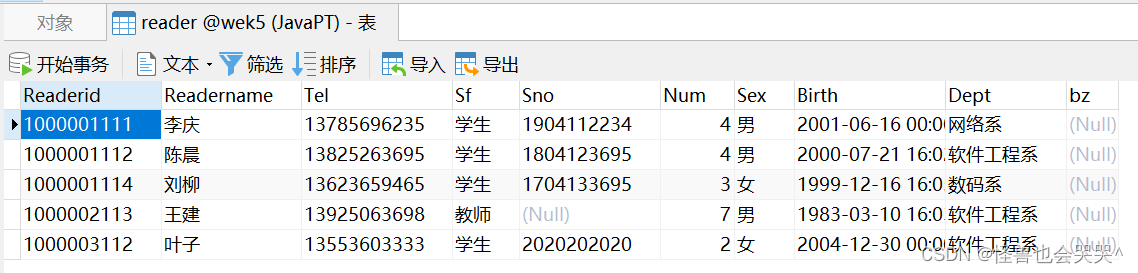
比如，这张reader表，其实就是一个关系数据模型。

（1）字段：

是二维表中的列。每个字段具有不同的名称，并且存储着对应数据的值。例如，在一个学生表中，字段可以是学生的姓名、年龄、性别等。

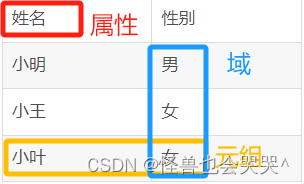
（2）属性

是指字段所描述的数据的特征或特性。它是对字段的进一步描述。例如，在学生表中，姓名字段的属性可以是字符串类型，长度不能超过20个字符。

（3）记录

是二维表中的行，包含了一组相关的数据。每一行代表了一个实体或对象，对应于现实世界中的一个个体。例如，在学生表中，每一行表示一个学生的信息，包括姓名、年龄、性别等。

（4）元组

是对记录的一种抽象，用来表示一组相关的数据。它是二维表的一个实例，可以看作是表中的一行。例如，如果学生表中有5个记录，那么可以说学生表包含了5个元组。

二、关系模型的数据结构和定义

1.域

域是一组具有相同数据类型的值的集合，又称为值域。在关系中是通过域来表示属性的取值范围;

域中所包含的值的个数称为域的基数（用m表示）

2.笛卡尔积

给定一组值可以相同的域D1,D2...Dn其笛卡尔积为：

$D1\times D2...\times Dn=\left \{ (d1,d2,...,dn)|di\in Di,i=1,2,...,n \right \}$

（1）笛卡尔积是一个集合，但可以用一个二维表来表示，是各集合各元素间一切可能的组合；

（2）每一个元素(d1，d2，…，dn)即任意一行，叫做一个n元组；元素中的值dn叫做一个分量；

（3）笛卡尔积的基数M（即元素d1，d2，…，dn的个数n）为所有域的基数的累乘之积，即

$M=\prod_{i-1}^{n}mi$ ? ? ? ? ?

（4）例题：给出分量小明、小王、小叶、男、女，要表示出这个学生关系中姓名和性别两个域的笛卡尔积：

$D1\times D2$ ={(小明，男),(小明，女),(小王，男),(小王，女),(小叶，男),(小叶，女)}
即 $M=m1\times m2=3\times 2=6$

3.关系

笛卡尔积D1×D2×…×Dn的任一子集称为定义在域D1，D2，…，Dn上的n元关系

$R(D1,D2,...,Dn)$

【R是关系的名字，n是关系的目或者度】

（1）关系是笛卡尔积的有限子集，是一张二维表。

（2）当n=1，表示单元关系；当n=2，表示二元关系；故而，n元关系就有n个属性。

（3）关系中的每一个元素是关系中的元组，通常以t来表示

（4）如上例题的 $D1\times D2$ 就可以构成一个学生关系：

姓名性别
小明男
小王女
小叶女

4.关系的性质：

关系是一种规范化了的二维表中行的集合

（1）关系中每一个属性值都具有原子性，都是不可分解的。

（2）每一列中的分量必须来自同一个域，必须是同一类型的数据。

（3）不同的列可来自同一个域，每一列称为属性，不同的属性必须有不同的名字。

（4）列的顺序可以任意交换。交换时属性名和属性值也要随之交换，否则得到的关系是不同的。

（5）关系中元组的顺序可任意交换，即任意交换行的位置是可以的。

（6）关系中不允许出现重复元组。

5.关系的码

关系的码	相关定义性质
主码（Primary Key）	(1)关系模式中唯一标识每个元组的属性或属性组合。 (2)必须是唯一且非空的。 (3)一个关系可以有一个或多个主码(联合主键)。
外码（Foreign Key）	(1)关系模式中的属性，引用了另一个关系模式中的主码。 (2)用于建立关系模式之间的连接。 (3)值必须与关联关系的主码值保持一致，或者为空（NULL）。
候选码（Candidate Key）	(1)可以成为主码的属性或属性组合，能够唯一标识关系中元组的一个属性或属性集。 (2) 必须是唯一且非空的。 (3)?一个关系可以有多个候选码，但只能选择其中一个作为主码。
超码（Super Key）	可以唯一标识每个元组的属性或属性组合，可能包含冗余属性。
主属性（Key Attribute）	构成主码的属性。
非主属性（Non-key Attribute）	非主码的属性。
复合属性（Composite Attribute）	由多个属性组成的属性。可以是主码、非主码或外码。
码的选择（Choosing Keys）	根据实际需求和业务规则选择适当的主码。主码应该是稳定的、唯一的、简单的以及易于管理和维护的。

三、关系完整性

关系模型中，完整性约束必须满足实体完整性和参照完整性，这是关系的两个不变性。

1.实体完整性

主码的值不能为空（字段只有一个时）或部分为空（联合主键）。

2.参照完整性

如果关系R2的外部关系键X与关系R1的主关系键相符，则X的每个值或者等于R1中主关系键的某一个值，或者取空值。简单来说就是，外键与其所在表的主键值要相同或者为空。

3.用户自定义完整性

针对某一具体应用所涉及的数据提出约束性条件。用户自定义完整性主要包括字段有效性约束和记录有效性。如：学生关系中的性别属性的取值范围在男-女之间。

四、关系操作——关系代数

关系代数的运算按运算符的不同主要分为两类：

1.传统的集合运算

（1）概念：

把关系看成元组的集合，其运算是从关系的“水平”方向即行的角度进行的。包括并、差、交和笛卡尔积等运算。

（2）运算种类：

操作	表达式	描述
并	R ∪ S = {t \| t ∈ R ∨ t ∈ S}	合并关系R和关系S中的所有元组，得到一个包含两个关系中所有元组的新关系。
差	R - S = {t \| t ∈ R ∧ ?t ∈ S}	从关系R中删除所有在关系S中出现的元组，得到一个包含在R中但不在S中的所有元组的新关系。
交	R ∩ S = {t \| t ∈ R ∧ t ∈ S} R∩S = R-(R-S)	仅保留同时在关系R和关系S中出现的元组，得到一个包含同时在R和S中出现的所有元组的新关系。
广义笛卡尔积	R × S = {tr⌒ ts \| tr ∈ R ∧ ts ∈ S}	将关系R中的每个元组与关系S中的每个元组连接在一起，得到一个包含所有可能的元组组合的新关系。

（3）例题：???????

A	B	C
a1	b2	c1
a2	b1	c1
a2	b1	c2

A	B	C
a1	b2	c2
a2	b1	c1
a2	b1	c2

A	B	C
a1	b2	c1
a1	b2	c2
a2	b1	c1
a2	b1	c2

R ∪ S

A	B	C
a2	b1	c1
a2	b1	c2

R ∩ S???????

A	B	C
a1	b2	c1

R - S

A	B	C	A	B	C
a1	b2	c1	a1	b2	c2
a1	b2	c1	a2	b1	c1
a1	b2	c1	a2	b1	c2
a2	b1	c1	a1	b2	c2
a2	b1	c1	a2	b1	c1
a2	b1	c1	a2	b1	c2
a2	b1	c2	a1	b2	c2
a2	b1	c2	a2	b1	c1
a2	b1	c2	a2	b1	c2

???????R与S的???????广义笛卡尔积

2.专门的关系运算

（1）概念：

不仅涉及行运算，也涉及列运算，这种运算是为数据库的应用而引进的特殊运算。包括选取、投影、连接和除法等运算。

（2）运算种类：

关系运算

表达式

描述

选择 (σ)

$\sigma _{F}(R)={t|t\in R\wedge F(t)='true')}$

F为选取的条件

根据指定的条件，从关系中选择满足条件的元组，返回一个新的关系。选择是对行操作。

投影 (π)

$\Pi _{A}(R)={t[A] |t\in R}$

A为R中的属性列

从关系中选择指定的属性列，返回一个新的关系。

连接 (Join)

$\left (R\infty S \right )_{x\theta y}-\left \{ t_{r} \cap t_{s}| t_{r}\in R\wedge t_{s}\in S\wedge t_{r}[X]\theta t_{s}[Y]]\right \}$

θ是算术比较运算符
=	等值连接
<	小于连接
>	大于连接

也称为θ连接，是从两个关系的笛卡尔积中选取属性间满足连接条件的元组，组成新的关系。

自然连接 (?)

$R\triangleright \triangleleft S$

一种特殊的等值连接，?在等值连接的情况下，当连接属性X与Y具有相同属性组时，把在连接结果中重复的属性列去掉

除法 (/)

$R\div S=\left \{ tr[X] | tr\in R\wedge \Pi y(S)\subseteq Yx\right \}$

给定两个关系，计算满足第一个关系中的所有元组都与第二个关系中的某个属性值相关联的元组，并返回一个新的关系。

（3）例题：

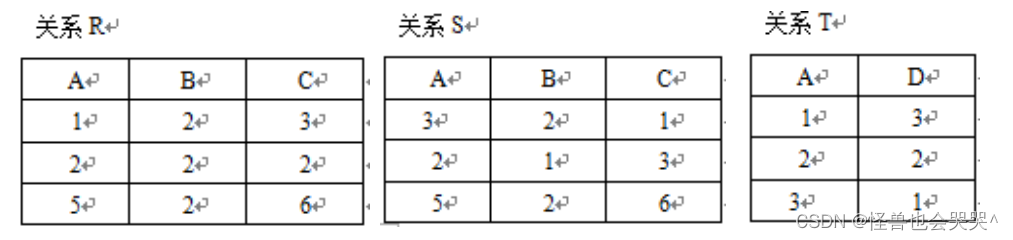
【1-1】设有以下关系R、S和T，求下列各关系代数的运算结果。

求??????? $\Pi _{A,B}(\sigma _{c=6}(R))$

第一步先求 $\sigma _{c=6}(R)$

A B C
5 2 6

第二步求 $\Pi _{A,B}(\sigma _{c=6}(R))$

A B
5 2

求 $\Pi _{B,C}(\sigma _{c=3}(S\triangleright \triangleleft T))$ ???????

第一步求 $S\triangleright \triangleleft T$

A B C A D
3 2 1 1 4
2 1 3 2 2
5 2 6 3 1

第二步求 $\sigma _{c=3}(S\triangleright \triangleleft T)$

A B C A D
2 1 3 2 2

第三步求 $\Pi _{B,C}(\sigma _{c=3}(S\triangleright \triangleleft T))$

B C
1 3

【1-2】设有关系R和S，求R÷S.???????

A

B

C

D

a2

b2

c1

d1

a1

b2

c2

d1

a1

b1

c1

d2

a2

b2

c3

d3

R

C

D

E

c1

d1

e1

c3

d3

e2

S

第一步：找到两个关系R与 S共同有的列

R.C

R.D
S.C S.D

c1

d1

c1

d1

c2

d1

c3

d3

c1

d2

c3

d3

第二步：在R表中找与S表中CD列取值相同的行

A

B

C

D

a2

b2

c1

d1

a2

b2

c3

d3

第三步：看看在R表是否能找到A、B列值所在行，是既包括{c1,d1}又包括{c3,d3}的

A

B

a2

b2???????

所以R÷ S的结果是：

A

B

a2

b2???????

文章来源:https://blog.csdn.net/ysy1119/article/details/135295888
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！

A	B	C	A	B	C
a1	b2	c1	a1	b2	c2
a1	b2	c1	a2	b1	c1
a1	b2	c1	a2	b1	c2
a2	b1	c1	a1	b2	c2
a2	b1	c1	a2	b1	c1
a2	b1	c1	a2	b1	c2
a2	b1	c2	a1	b2	c2
a2	b1	c2	a2	b1	c1
a2	b1	c2	a2	b1	c2

姓名	性别
小明	男
小王	女
小叶	女

A	B	C	A	B	C
a1	b2	c1	a1	b2	c2
a1	b2	c1	a2	b1	c1
a1	b2	c1	a2	b1	c2
a2	b1	c1	a1	b2	c2
a2	b1	c1	a2	b1	c1
a2	b1	c1	a2	b1	c2
a2	b1	c2	a1	b2	c2
a2	b1	c2	a2	b1	c1
a2	b1	c2	a2	b1	c2

《数据库系统原理》之关系数据库 【知识点罗列+关系代数例题演练】

一、关系模型

1.什么是数据模型？

2.什么是关系模型?

（1）字段：

（2）属性

（3）记录

（4）元组

二、关系模型的数据结构和定义

1.域

2.笛卡尔积

3.关系

4.关系的性质 ：

5.关系的码

三、关系完整性

1.实体完整性

2.参照完整性

3.用户自定义完整性

四、关系操作——关系代数

1.传统的集合运算

（1）概念：

（2）运算种类：

（3）例题：???????

2.专门的关系运算

（1）概念：

（2）运算种类：

（3）例题：

《数据库系统原理》之关系数据库【知识点罗列+关系代数例题演练】

4.关系的性质：

A	B	C	A	B	C
a1	b2	c1	a1	b2	c2
a1	b2	c1	a2	b1	c1
a1	b2	c1	a2	b1	c2
a2	b1	c1	a1	b2	c2
a2	b1	c1	a2	b1	c1
a2	b1	c1	a2	b1	c2
a2	b1	c2	a1	b2	c2
a2	b1	c2	a2	b1	c1
a2	b1	c2	a2	b1	c2