写递归函数的一些思考
发布时间:2023年12月17日
当编写递归函数时,有几个关键的思考点可以帮助你设计和实现递归算法:
-
定义递归的基本情况:确定递归函数应该在何时终止,即递归的基本情况。这是一个递归的出口条件,确保递归不会无限进行下去。基本情况应该是可以直接求解或返回的简单情况。
-
确定递归的问题规模:考虑如何将原问题分解为规模更小的子问题。递归函数应该在每一次递归调用时减小问题的规模,使得递归最终会达到基本情况。
-
利用递归调用解决子问题:在递归函数中调用自身来解决子问题。递归调用应当是朝着基本情况逼近的方向进行的,以确保问题规模不断缩小。
整合子问题的结果:在递归函数中,将子问题的解合并为原问题的解。这可能涉及到对子问题结果的处理、组合、计算等操作,以获得最终的结果。
无论是表格路径搜索的dfs,还是说其他的递归问题,都可以用这一套思想来处理,下面的题目是695. 岛屿的最大面积做路径搜索dfs的例子
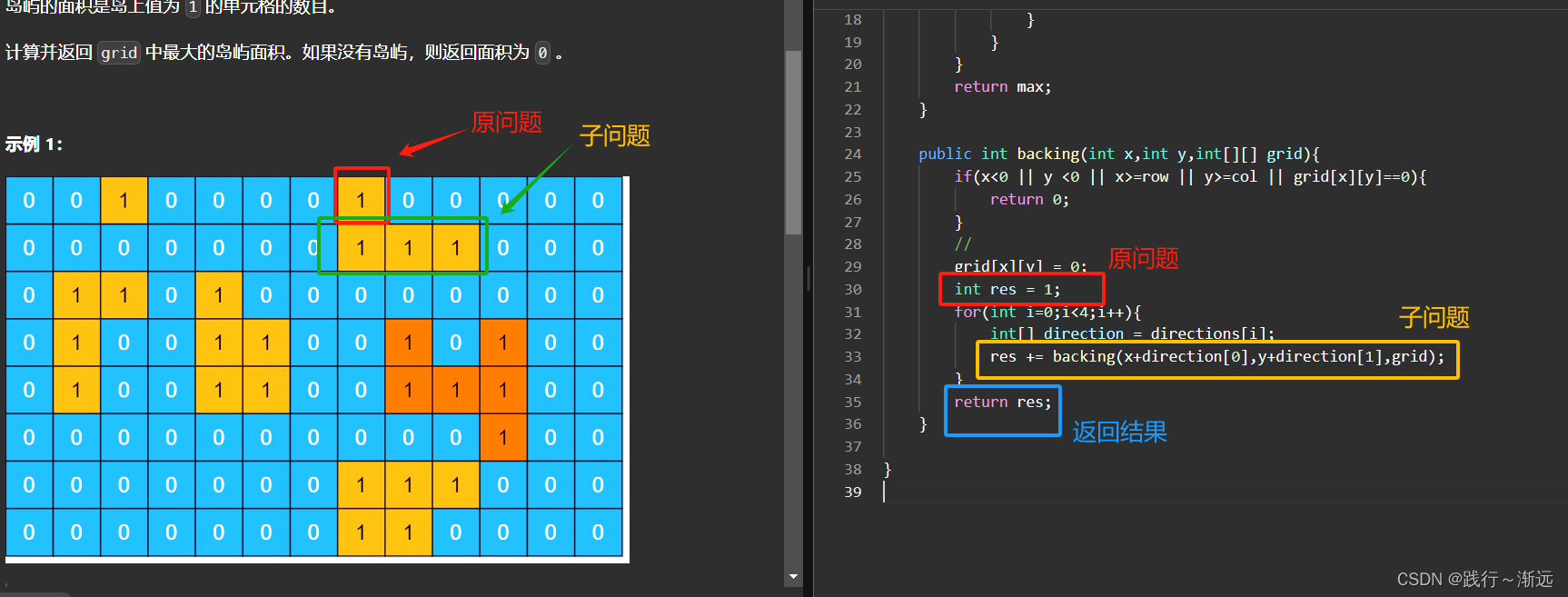
我的小思考就是:最直接的想法就是:想清楚你写的递归函数的作用是什么,自然而然也就能写出清晰明了的递归函数了。
比如对于上方的代码,我的backing递归函数的作用就是返回我能走过路的最大路长(面积)【一路走到黑】;因此对于子问题的处理我只需要交给backing函数,而对于原问题的处理,我只需要在已有的步长1的基础上,加上子问题返回的backing即可,最终返回我的答案res,也就是上面图片所示。
附上完整代码
class Solution {
int[][] directions = new int[][]{
{-1,0},
{1,0},
{0,1},
{0,-1}
};
int row;
int col;
public int maxAreaOfIsland(int[][] grid) {
row = grid.length;
col = grid[0].length;
int max = 0;
for(int i=0;i<row;i++){
for(int j=0;j<col;j++){
if(grid[i][j]==1){
max = Math.max(max,backing(i,j,grid));
}
}
}
return max;
}
public int backing(int x,int y,int[][] grid){
if(x<0 || y <0 || x>=row || y>=col || grid[x][y]==0){
return 0;
}
//
grid[x][y] = 0; //防止重复走绕圈情况,也可以单独用一个visited[][]标记
int res = 1; //能走到这里,说明grid[x][y]==1
for(int i=0;i<4;i++){
int[] direction = directions[i];
res += backing(x+direction[0],y+direction[1],grid);
}
return res;
}
}
其他问题的迁移 【 463. 岛屿的周长】
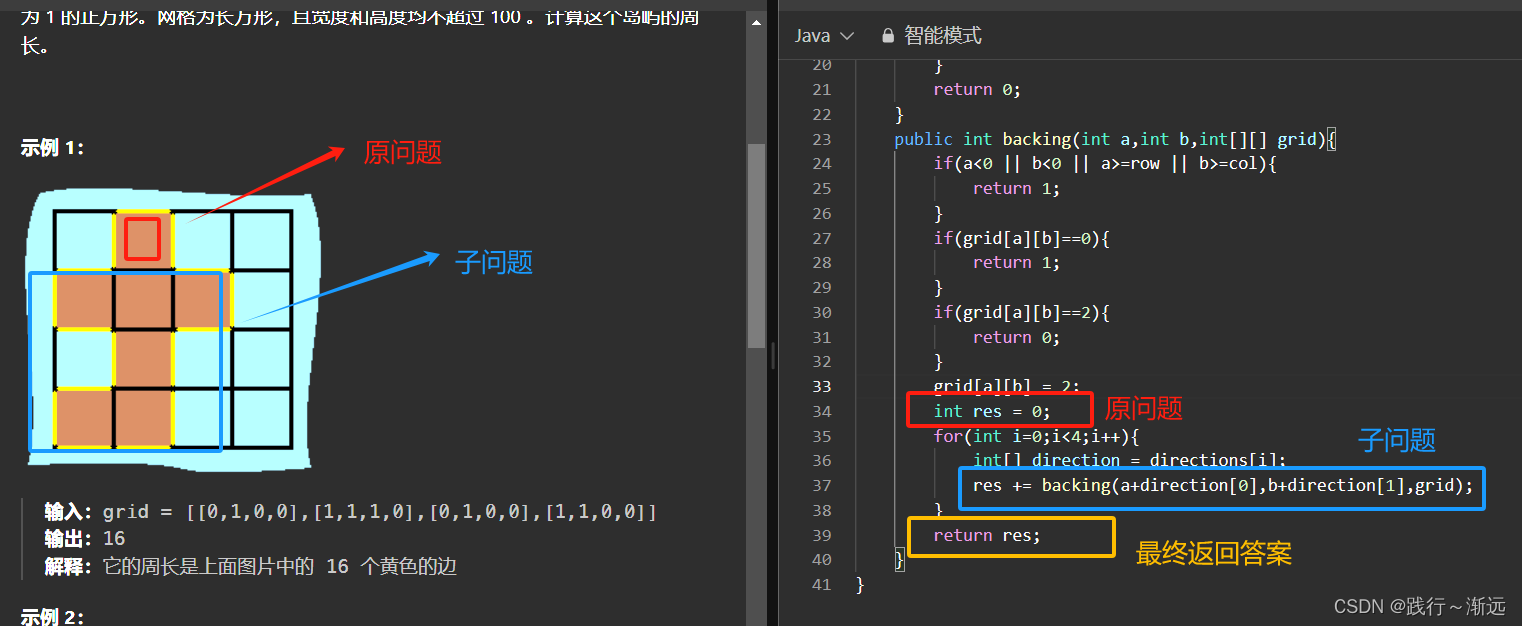
文章来源:https://blog.csdn.net/m0_46542703/article/details/135045616
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- java基于Spring Boot+vue的学生宿舍管理系统qkc37
- 52.常用shell之 gzip / gunzip - 压缩和解压文件 的用法及衍生用法
- 从方程到预测:数学在深度学习中的作用
- Bezier 曲线 2D
- docker部署ng实现反向代理
- ARP协议详解(产生背景/类型/报文/工作原理)
- 郑州工商学院实验室设备管理系统(源码+开题报告)
- Mybatis中查询今天、本周、本月、半年、一年等数据
- C#基础——文件、文件夹操作和序列化存储
- 9-1,ZZ004 新型电力系统运行与维护赛题第九套