2024华数杯A题高质量成品论文+完整数据py代码+来源数据集+参考文献

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?A题日本排核废水（完整数据代码在文末）

#### 1. 时变因素：

- Tritium 浓度的时变因素包括排放时间、排放量、海水运动等。需要考虑问题陈述中给出的放射性废水排放计划（Appendix）。

#### 2. 海洋环境因素：

- Tritium 浓度的分布受到海洋环境因素的影响，如水流、潮汐、季节性变化等。可以考虑使用流体动力学模型来模拟 Tritium 在海水中的传播。

#### 3. Tritium 吸收和释放：

- Tritium 会被海洋生物吸收，并随着食物链传递。考虑 Tritium 在不同海洋生物体内的累积和释放，以及这些生物的迁徙等因素。

#### 4. 空间分布分析：

- 利用模型或数值方法，模拟 Tritium 浓度在海水中的空间分布。可以将海域划分为网格，使用扩散方程模拟 Tritium 的传播。

#### 5. 时序分析：

- 对 Tritium 浓度进行时序分析，观察 Tritium 浓度随时间的变化。可以利用数值模拟的结果，得到 Tritium 浓度在不同海域的演化情况。

#### 6. 数据收集与验证：

- 收集实际监测数据，验证模型的准确性。对比模型预测结果与实际观测结果，调整模型参数以提高预测精度。

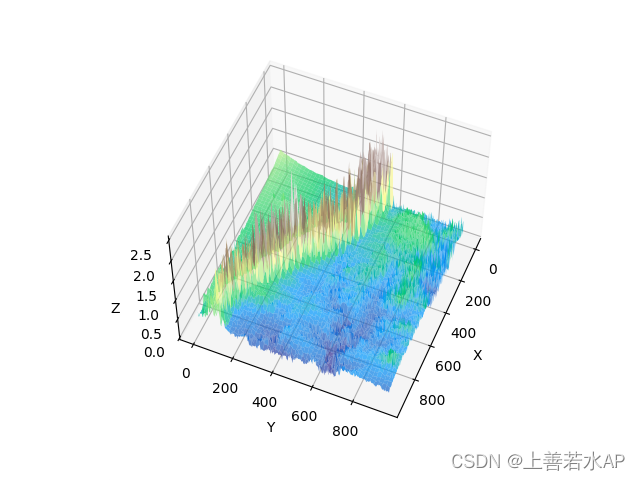
#### 7. 空间可视化：

- 利用地理信息系统 (GIS) 等工具，将 Tritium 浓度的空间分布进行可视化。这有助于直观理解 Tritium 污染的分布情况。

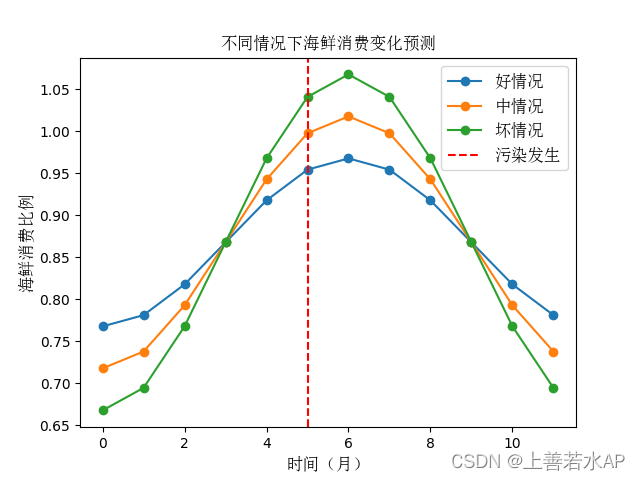
#### 8. 预测未来情景：

- 根据模型的预测能力，尝试预测未来 Tritium 浓度的分布情景。考虑可能的变化因素，如气候变化、人类活动等。

### Tritium 浓度的模型方程（简化）：

$$\frac{\partial C}{\partial t} = D \left(\frac{\partial^2 C}{\partial x^2} + \frac{\partial^2 C}{\partial y^2}\right) + \text{Sources and Sinks}$$

其中：

- \(C\) 是 Tritium 浓度。

- \(D\) 是 Tritium 在海水中的扩散系数。

- "Sources and Sinks" 表示 Tritium 的来源和汇，包括废水排放、生物吸收等。

```python

import numpy as np

import matplotlib.pyplot as plt

from scipy.sparse import coo_matrix, kron, eye

from scipy.sparse.linalg import spsolve

def assemble_system_matrices(num_elements, D, L):

????h = L / num_elements

????nodes = num_elements + 1

????

????# 1D stiffness matrix

????K1D = coo_matrix(([-1, 2, -1], (range(nodes-1), range(1, nodes))), shape=(nodes, nodes)).tocsr()

????

????# 2D stiffness matrix

????K2D = kron(eye(nodes), K1D) + kron(K1D, eye(nodes))

????

????# Mass matrix

????M = coo_matrix(([h/6, 2*h/3, h/6] * num_elements, (np.repeat(range(num_elements), 3),

????????????????????????????????????????????????????????np.tile(range(nodes), num_elements))), shape=(nodes, nodes)).tocsr()

????

????# Diffusion matrix

????A = D * K2D

????

????return M, A

def solve_diffusion_equation(num_elements, D, L, num_steps, dt, initial_condition):

????M, A = assemble_system_matrices(num_elements, D, L)

????

????nodes = num_elements + 1

????C = np.zeros((nodes, num_steps))

????C[:, 0] = initial_condition

????

????for n in range(1, num_steps):

????????# Time-stepping using implicit Euler method

????????C[:, n] = spsolve(M + dt * A, M @ C[:, n-1])

????

????return C

# Parameters

num_elements = 100

D = 0.01

L = 200

num_steps = 200

dt = 0.1

# Initial condition (Gaussian pulse)

点击链接加入群聊【2024华数杯数学建模】：