KMP算法

KMP算法的用处

KMP主要应用在字符串匹配上。

用暴力解法的字符串匹配：

class Solution {
    // 定义一个方法，接收两个字符串参数：haystack和needle
    public int strStr(String haystack, String needle) {
        // 获取haystack的长度n，以及needle的长度m
        int n = haystack.length(), m = needle.length();
        // 遍历haystack，从0开始，直到i + m <= n
        for (int i = 0; i + m <= n; i++) {
            // 定义一个布尔变量flag，初始值为true
            boolean flag = true;
            // 遍历needle，从0开始，直到j < m
            for (int j = 0; j < m; j++) {
                // 如果haystack中第i+j个字符与needle中第j个字符不相等
                if (haystack.charAt(i + j) != needle.charAt(j)) {
                    // 将flag设为false，并跳出内层循环
                    flag = false;
                    break;
                }
            }
            // 如果flag为true，说明找到了匹配的子串，返回当前索引i
            if (flag) {
                return i;
            }
        }
        // 如果没有找到匹配的子串，返回-1
        return -1;
    }
}

每次匹配都从模式串的开头开始，时间复杂度为O（n*m）

KMP的经典思想就是:当出现字符串不匹配时，可以记录一部分之前已经匹配的文本内容，利用这些信息避免从头再去做匹配。

前缀表（next数组）

next数组，即前缀表，记录了模式串与主串不匹配时，模式串一个从哪开始重新匹配

举一个例子：

要在文本串：aabaabaafa 中查找是否出现过一个模式串：aabaaf。

文本串中第六个字符b 和 模式串的第六个字符f，不匹配了。如果暴力匹配，发现不匹配，此时就要从头匹配了。

但如果使用前缀表，就不会从头匹配，而是从上次已经匹配的内容开始匹配，找到了模式串中第三个字符b继续开始匹配。

在某个字符失配时，前缀表会告诉你下一步匹配中，模式串应该跳到哪个位置。

那么什么是前缀表：记录下标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。

最长相同前后缀

前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串。

后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。

?前缀表要求的就是相同前后缀的长度。

字符串a的最长相等前后缀为0。 字符串aa的最长相等前后缀为1。 字符串aaa的最长相等前后缀为2。 等等.....。

前缀表的作用

匹配的过程在下标5的地方遇到不匹配，模式串是指向f，如图：?

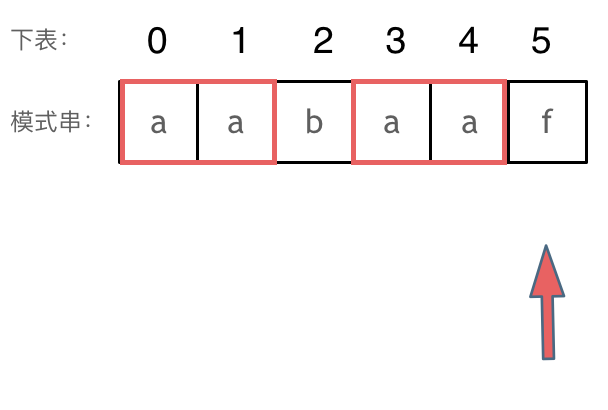
然后就找到了下标2，指向b，继续匹配：如图：?

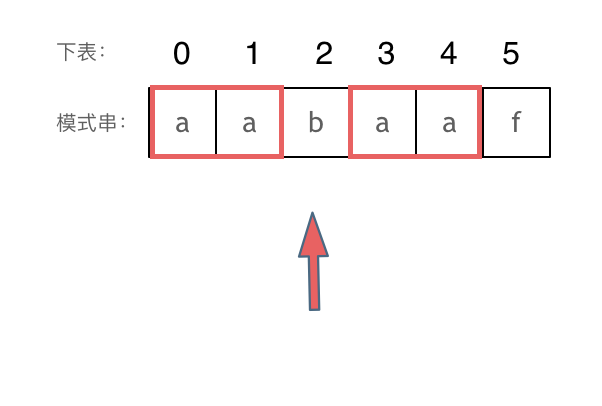
以下这句话，对于理解为什么使用前缀表可以告诉我们匹配失败之后跳到哪里重新匹配 非常重要！

下标5之前这部分的字符串（也就是字符串aabaa）的最长相等的前缀 和 后缀字符串是 子字符串aa ，因为找到了最长相等的前缀和后缀，匹配失败的位置是后缀子串的后面，那么我们找到与其相同的前缀的后面重新匹配就可以了。

所以前缀表具有告诉我们当前位置匹配失败，跳到之前已经匹配过的地方的能力。

计算前缀表

如图：

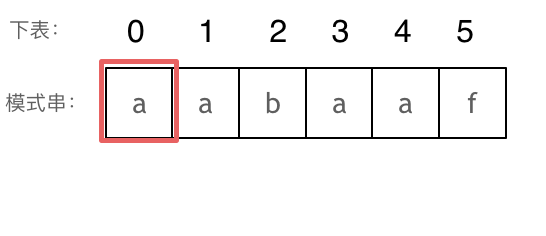
长度为前1个字符的子串a，最长相同前后缀的长度为0。（注意字符串的前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串；后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。）

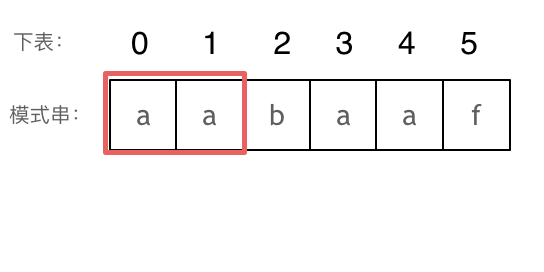
长度为前2个字符的子串aa，最长相同前后缀的长度为1。

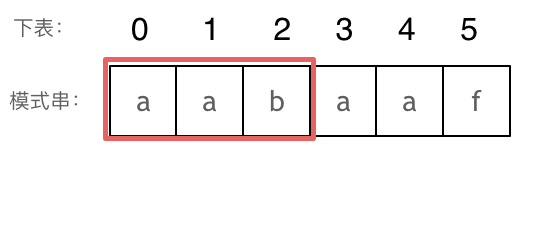
长度为前3个字符的子串aab，最长相同前后缀的长度为0。

以此类推： 长度为前4个字符的子串aaba，最长相同前后缀的长度为1。 长度为前5个字符的子串aabaa，最长相同前后缀的长度为2。 长度为前6个字符的子串aabaaf，最长相同前后缀的长度为0。

那么把求得的最长相同前后缀的长度就是对应前缀表的元素，如图：?

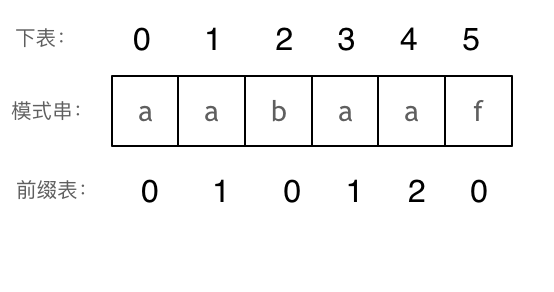
可以看出模式串与前缀表对应位置的数字表示的就是：下标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。

再来看一下如何利用 前缀表找到 当字符不匹配的时候应该指针应该移动的位置。如动画所示：

找到的不匹配的位置， 那么此时我们要看它的前一个字符的前缀表的数值是多少。

为什么要前一个字符的前缀表的数值呢，因为要找前面字符串的最长相同的前缀和后缀。

所以要看前一位的 前缀表的数值。

前一个字符的前缀表的数值是2， 所以把下标移动到下标2的位置继续比配。 可以再反复看一下上面的动画。

最后就在文本串中找到了和模式串匹配的子串了。

前缀表与next数组

KMP算法的实现都是使用next数组来做回退再匹配操作

next数组就可以是前缀表，但是很多实现都是把前缀表统一减一（右移一位，初始位置为-1）之后作为next数组。

next数组既可以就是前缀表，也可以是前缀表统一减一（右移一位，初始位置为-1），这只是具体实现的区别。

使用next数组来匹配

以下我们以前缀表统一减一之后的next数组来做演示。

有了next数组，就可以根据next数组来 匹配文本串s，和模式串t了。

注意next数组是新前缀表（旧前缀表统一减一了）。

匹配过程动画如下：

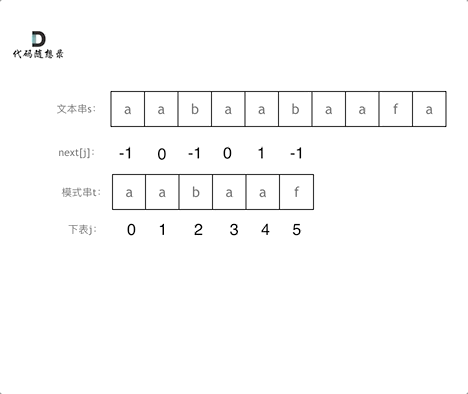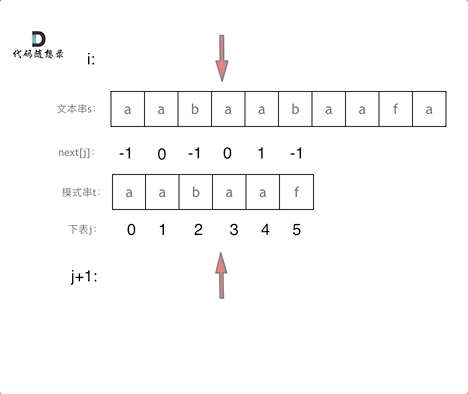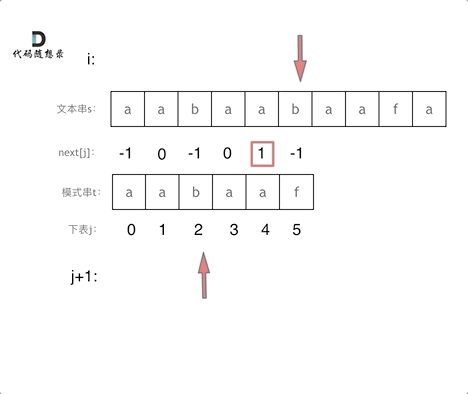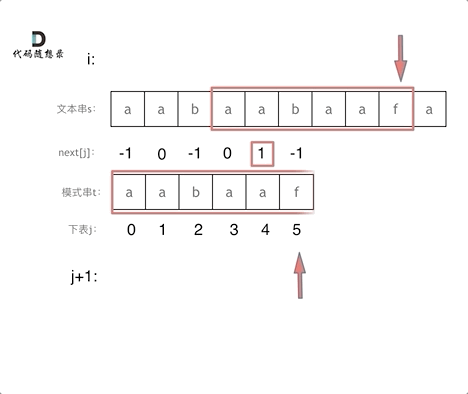
时间复杂度分析

其中n为文本串长度，m为模式串长度，因为在匹配的过程中，根据前缀表不断调整匹配的位置，可以看出匹配的过程是O(n)，之前还要单独生成next数组，时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。

暴力的解法显而易见是O(n × m)，所以KMP在字符串匹配中极大地提高了搜索的效率。

为了和力扣题目28.实现strStr保持一致，方便大家理解，以下文章统称haystack为文本串, needle为模式串。

都知道使用KMP算法，一定要构造next数组。

计算next数组

感觉next数组作为前缀表统一减一很不舒服，这里统一写成原前缀表的形式

private void getNext(int[] next, String s) {
    int j = 0; // 初始化j为0，表示当前前缀末尾的位置
    next[0] = 0; // 将next数组的第一个元素设为0，表示长度为1字符串的相同前缀后缀长度为0
    for (int i = 1; i < s.length(); i++) { // 从第二个字符开始遍历字符串，i是后缀末尾
        while (j > 0 && s.charAt(j) != s.charAt(i)) { // 如果j大于0且当前字符与j位置的字符不相等(前缀末尾与后缀末尾不相同)
            j = next[j - 1]; // 更新j的值，j等于前一个next值
        }
        if (s.charAt(j) == s.charAt(i)) { // 如果当前字符与j位置的字符相等
            j++; // j自增1（求的是前缀的长度，索引要加一）
        }
        next[i] = j; // 将当前j值赋给next数组的第i个元素
    }
}

?28.找出字符串中第一个匹配项的下标

28. 找出字符串中第一个匹配项的下标

简单

给你两个字符串?haystack?和?needle?，请你在?haystack?字符串中找出?needle?字符串的第一个匹配项的下标（下标从 0 开始）。如果?needle?不是?haystack?的一部分，则返回??-1?。

示例 1：

输入：haystack = "sadbutsad", needle = "sad"
输出：0
解释："sad" 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ，所以返回 0 。

示例 2：

输入：haystack = "leetcode", needle = "leeto"
输出：-1
解释："leeto" 没有在 "leetcode" 中出现，所以返回 -1 。

提示：

• 1 <= haystack.length, needle.length <= 104
• haystack?和?needle?仅由小写英文字符组成

class Solution {
    //前缀表（不减一）Java实现
    public int strStr(String haystack, String needle) {
        // 如果needle为空字符串，返回0
        if (needle.length() == 0) return 0;
        // 初始化next数组
        int[] next = new int[needle.length()];
        // 获取next数组
        getNext(next, needle);

        int j = 0;
        // 遍历haystack字符串
        for (int i = 0; i < haystack.length(); i++) {
            // 当j大于0且当前字符与needle中的字符不相等时，更新j的值
            while (j > 0 && needle.charAt(j) != haystack.charAt(i)) 
                j = next[j - 1];
            // 当当前字符与needle中的字符相等时，j自增1
            if (needle.charAt(j) == haystack.charAt(i)) 
                j++;
            // 如果j等于needle的长度，说明找到了匹配的子串，返回子串在haystack中的起始位置
            if (j == needle.length()) 
                return i - needle.length() + 1;
        }
        // 如果没有找到匹配的子串，返回-1
        return -1;

    }
    
    // 获取next数组的方法
    private void getNext(int[] next, String s) {
        int j = 0;
        next[0] = 0;
        // 遍历字符串s
        for (int i = 1; i < s.length(); i++) {
            // 当j大于0且当前字符与s中的字符不相等时，更新j的值
            while (j > 0 && s.charAt(j) != s.charAt(i)) 
                j = next[j - 1];
            // 当当前字符与s中的字符相等时，j自增1
            if (s.charAt(j) == s.charAt(i)) 
                j++;
            // 将j的值赋给next数组的第i个元素
            next[i] = j; 
        }
    }
}