算法设计与分析复习笔记第六章分支限界法

分支限界法概述

分支限界法的基本思想

分支限界法类似于回溯法，也是一种在问题的解空间树T中搜索问题解的算法。

但在一般情况下，分枝限界法与回溯法的求解目标不同。回溯法的求解目标是找出解空间树中满足约束条件的所有解，而分枝限界法的求解目标则是找出满足约束条件的一个解，或是在满足约束条件的解中找出使某一目标函数值达到极大或极小的解，即在某种意义下的最优解。

所谓“分枝”就是采用广度优先的策略，依次搜索活结点的所有分枝，也就是所有相邻结点。
?

求最优解时，选择哪一个子结点？
采用一个限界函数，计算限界函数值，选择一个最有利的子结点作为扩展结点，使搜索朝着解空间树上有最优解的分枝推进，以便尽快地找出一个最优解。

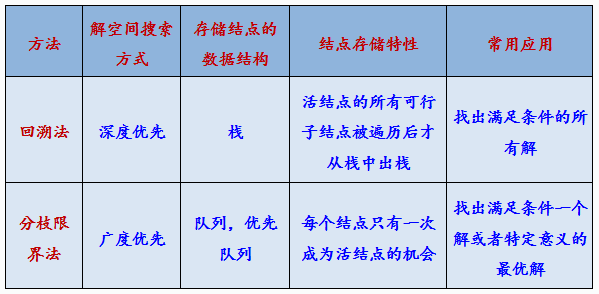
分支限界法与回溯法的主要区别

分支限界法的设计思想

1. 设计合适的限界函数
2. 组织活结点表
3. 确定最优解的解向量

1. 设计合适的限界函数

在搜索解空间树时，每个活结点可能有很多孩子结点，其中有些孩子结点搜索下去是不可能产生问题解或最优解的。可以设计好的限界函数在扩展时删除这些不必要的孩子结点，从而提高搜索效率。　　

假设活结点si有4个孩子结点，而满足限界函数的孩子结点只有2个，可以删除这2个不满足限界函数的孩子结点，使得从si出发的搜索效率提高一倍。

限界函数设计难以找出通用的方法，需根据具体问题来分析。一般地，先要确定问题解的特性：

目标函数是求最大值：则设计上界限界函数ub（根结点的ub值通常大于或等于最优解的ub值），若si是sj的父结点，应满足ub(si)≥ub(sj)，当找到一个可行解ub(sk)后，将所有小于ub(sk)的结点剪枝。

目标函数是求最小值：则设计下界限界函数lb（根结点的lb值一定要小于或等于最优解的lb值），若si是sj的父结点，应满足lb(si)≤lb(sj)，当找到一个可行解lb(sk)后，将所有大于lb(sk)的结点剪枝。

2.组织活结点表

根据选择下一个扩展结点的方式来组织活结点表，不同的活结点表对应不同的分枝搜索方式。

（1）队列式分枝限界法　　队列式分枝限界法将活结点表组织成一个队列，并按照队列先进先出（FIFO）原则选取下一个结点为扩展结点。步骤如下：

1将根结点加入活结点队列。

2从活结点队中取出队头结点，作为当前扩展结点。

3对当前扩展结点，先从左到右地产生它的所有孩子结点，用约束条件检查，把所有满足约束条件的孩子结点加入活结点队列。

4重复步骤②和③，直到找到一个解或活结点队列为空为止。

（2）优先队列式分枝限界法　　优先队列式分枝限界法的主要特点是将活结点表组组成一个优先队列，并选取优先级最高的活结点成为当前扩展结点。步骤如下：

1计算起始结点（根结点）的优先级并加入优先队列（与特定问题相关的信息的函数值决定优先级）。

2从优先队列中取出优先级最高的结点作为当前扩展结点，使搜索朝着解空间树上可能有最优解的分枝推进，以便尽快地找出一个最优解。

3对当前扩展结点，先从左到右地产生它的所有孩子结点，然后用约束条件检查，对所有满足约束条件的孩子结点计算优先级并加入优先队列。

4重复步骤②和③，直到找到一个解或优先队列为空为止。

3. 确定最优解的解向量

分枝限界法在搜索解空间树时，结点的处理是跳跃式的，回溯也不是单纯地沿着父结点一层一层地向上回溯，因此当搜索到某个叶子结点且该结点对应一个可行解时，如何得到对应的解向量呢？

两种方法：

① 对每个扩展结点保存从根结点到该结点的路径。　 每个结点带有一个可能的解向量。这种做法比较浪费空间，但实现起来简单，后面的示例均采用这种方式。

② 在搜索过程中构建搜索经过的树结构。 每个结点带有一个双亲结点指针，当找到最优解时，通过双亲指针找到对应的最优解向量。这种做法需保存搜索经过的树结构，每个结点增加一个指向双亲结点的指针。

采用分枝限界法求解的3个关键问题如下：

（1）如何确定合适的限界函数。
（2）如何组织待处理结点的活结点表。
（3）如何确定解向量的各个分量。

分枝限界法的时间性能

一般情况下，在问题的解向量X=（x1，x2，…，xn）中，分量xi（1≤i≤n）的取值范围为某个有限集合Si=（si1，si2，…，sir）。

问题的解空间由笛卡尔积S1×S2×…×Sn构成：

在最坏情况下，时间复杂性是指数阶。

0-1背包问题

实例：假设有4个物品，其重量分别为(4, 7, 5, 3)，价值分别为(40, 42, 25, 12)，背包容量W=10。将给定物品按单位重量价值从大到小排序，结果如下：

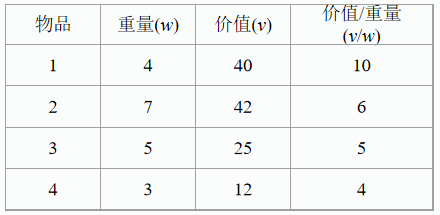
v/w:单位重量对应的价值

分析

问题的解可表示为n元向量{x1, x2, ... xn }, xi属于{0,1}，则可用子集树表示解空间。

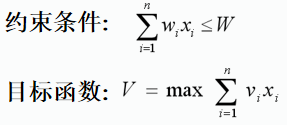
分支限界法：广度优先，约束条件，目标函数，上界函数，下界函数

上下界

贪心法的解(1,0,0,0)，价值为40，可作为0/1背包的下界。

上界ub可用最好情况来代替ub=w*(v1/w1)=10*10=100

目标函数的界[40, 100]，一般解空间树中第i层的各结点，代表对物1~i的选择，可这样定限界函数：

分支限界法求解0/1背包问题

目标函数是求最大值：则设计上界限界函数ub（根结点的ub值通常大于或等于最优解的ub值），若si是sj的父结点，应满足ub(si)≥ub(sj)，当找到一个可行解ub(sk)后，将所有小于ub(sk)的结点剪枝。

0/1背包问题 总结

从0/1背包问题的搜索过程可看出：与回溯法相比，分支限界法可根据限界函数不断调整搜索方向，选择最可能得最优解的子树优先进行搜索->找到问题的解。

0/1背包问题分支限界法伪代码

1．根据限界函数确定目标函数的界[down, up]；

2．将待处理结点表PT初始化为空；

3．对根结点的每个孩子结点x执行下列操作

3.1 估算结点x的目标函数值value;
3.2 若(value>=down)，则将结点x加入表PT中；

4．循环直到某个叶子结点的目标函数值在表PT中最大

4.1 i=表PT中值最大的结点；
4.2 对结点i的每个孩子结点x执行下列操作
4.2.1 估算结点x的目标函数值value;
4.2.2 若(value>=down)，则将结点x加入表PT中；
4.2.3 若(x是叶子结点且结点x的value值在表PT中最大), 则将结点x对应的解输出，算法结束；
4.2.4 若(结点x是叶子结点但结点x的value值在表PT中不是最大)，则令down=value，并且将表PT中所有小于value的结点删除；

应用分支限界法的其他关键问题：

如何确定最优解中的各个分量？

对每个扩展结点保存根结点到该结点的路径；例如，0/1背包问题。将部分解(x1, …, xi)和该部分解的目标函数的上界值都存储在待处理结点表中，在搜索过程中PT表的状态如下：

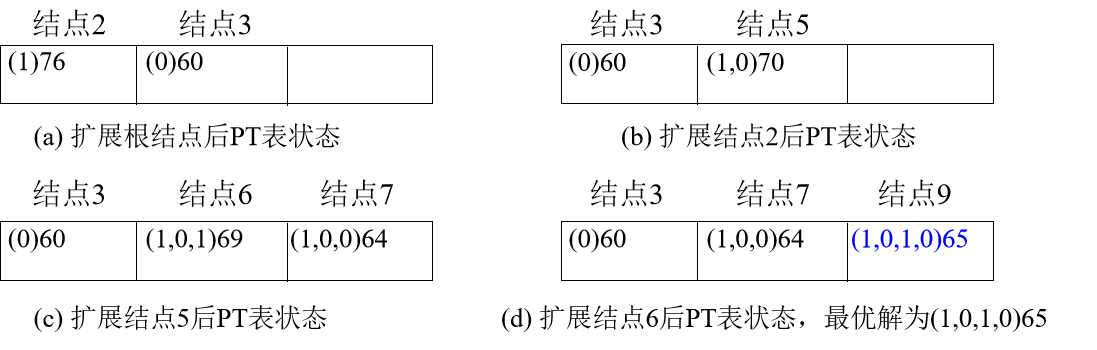
在搜索的过程中构建搜索经过的树结构，在求得最优解时，从叶子结点不断回溯到根结点，以确定最优解中的各个分量。

例如， 0/1背包问题。设一个表ST，在表PT中取出最大值结点进行扩充时，将最大值结点存储到表ST中，表PT和表ST的数据结构为(物品i-1的选择结果，<物品i, 物品i的选择结果>ub)，在搜索过程中表PT和表ST的状态如下：

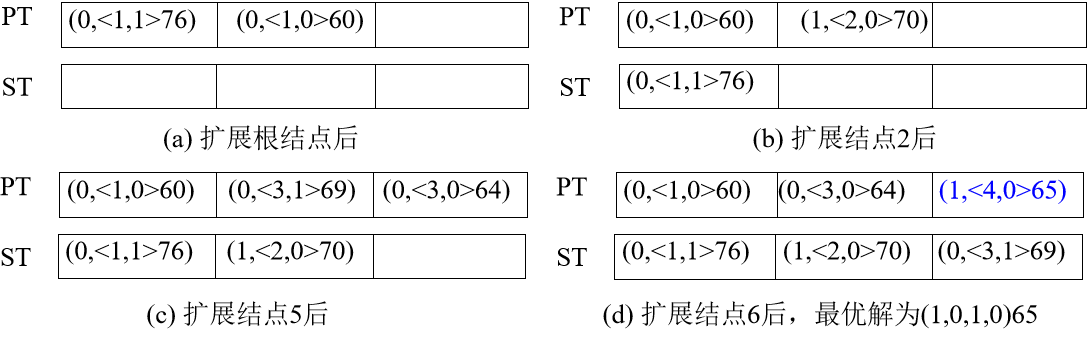
ST中记录的就是得到最优解的搜索路径上的各个结点！

0-1背包问题的算法思想

首先，要对输入数据进行预处理，将各物品依其单位重量价值从大到小进行排列。

节点的优先级由已装袋的物品价值加上剩下的最大单位重量价值的物品装满剩余容量的价值和。

算法首先检查当前扩展结点的左儿子结点的可行性。如果该左儿子结点是可行结点，则将它加入到子集树和活结点优先队列中。当前扩展结点的右儿子结点一定是可行结点，仅当右儿子结点满足上界约束时才将它加入子集树和活结点优先队列。当扩展到叶节点时为问题的最优值。

练习题

分别用回溯法和分支限界法界以下0/1背包问题三个物品的重量为{5, 7, 6}，价值为{10, 21, 24}，背包容量为 12 。

分支限界法与回溯法的区别

求解目标不同：

回溯法——找出满足约束条件的所有解
分支限界法——找出满足条件的一个解，或某种意义下的最优解

搜索方式不同：

回溯法——深度优先
分支限界法——广度优先或最小耗费优先

此外，在分支限界法中，每一个活结点只有一次机会成为扩展结点。

装载问题

问题描述

有一批共n个集装箱要装上2艘载重量分别为c1和c2的轮船，其中集装箱i的重量为wi，且

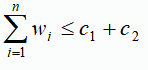
装载问题要求确定是否有一个合理的装载方案可将这个集装箱装上这2艘轮船。如果有，找出一种装载方案。

分析

把问题转换成一艘船的装货问题，即：第一艘船尽量多装，剩余的装入第二艘船

用子集树表示解空间：4层代表有3个货物，1代表装货物，2代表不装货物

解空间：X=(x1, x2 ,…, xn)，xi∈Si={0, 1}，i=1,2,…,n

约束函数：

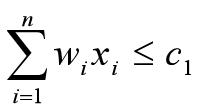
目标函数：

目标函数：
下界：…
上界：…

上限界函数：

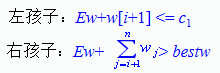
搜索算法设计

队列式分支限界：

优先队列式分支限界：

采用最大优先队列存储活结点表。活结点x在优先队列中的优先级定义为：从根结点到结点x的路径所相应的载重量Ew + 剩余集装箱的重量r。

子集树中叶结点所相应的载重量与其优先级相同，一旦有一个叶结点成为当前扩展结点，则可以断言该叶结点所相应的解即为最优解。此时可终止算法。

实现方法：(PT表结点的结构)

在活结点中保存从解空间树的根结点到该活结点的路径；

搜索进程中保存当前已构造出的部分解空间树；

旅行商问题

问题描述：略。

各个城市间的距离用代价矩阵来表示, 如果(i,j)不属于E，则cij=∞。

分析：设城市按自然数1, 2, ..., n编号

解空间树是一个排列树

n-1层作为叶子结点层

解向量：(x1, x2, ..., xn)

约束条件：
显式约束：xi=1, 2, ..., n (i=1, 2, ..., n)
隐式约束：(xi≠xj) ∧(cij≠∞)

问题分析

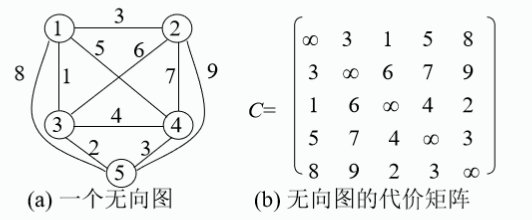
问题的上限：采用贪心法求得近似解为1→3→5→4→2→1，其路径长度为1+2+3+7+3=16

问题的下限：
1.把矩阵中每一行最小的元素相加，可以得到一个简单的下界，其路径长度为1+3+1+3+2=10，但是还有一个信息量更大的下界
2.考虑一个TSP问题的完整解，在每条路径上，每个城市都有两条邻接边，一条是进入这个城市的，另一条是离开这个城市的，那么，如果把矩阵中每一行最小的两个元素相加再除以2，如果图中所有的代价都是整数，再对这个结果向上取整，就得到了一个合理的下界。 db=((1+3)+(3+6)+(1+2)+(3+4)+(2+3))/2=14。需要强调的是，这个解并不是一个合法的选择（可能没有构成哈密顿回路），它仅仅给出了一个参考下界。

目标函数：

下限界函数：设已确定的顶点集合U=(r1, r2, ..., rk)

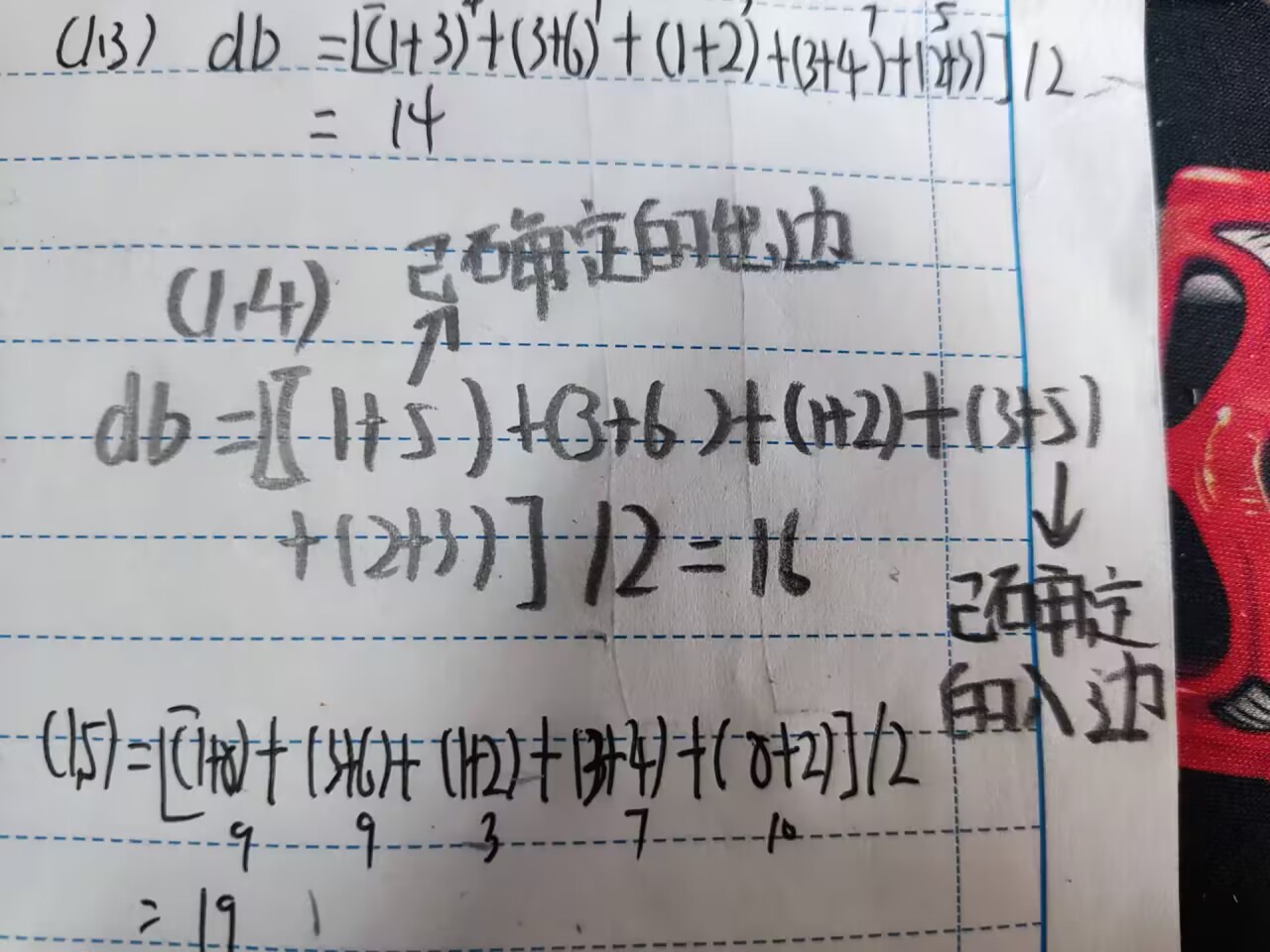
批处理作业调度问题

问题描述：给定n个作业的集合J={J1, J2, …, Jn}，每个作业都有3项任务分别在3台机器上完成，作业Ji需要机器j的处理时间为tij(1≤i≤n, 1≤j≤3)，每个作业必须先由机器1处理，再由机器2处理，最后由机器3处理。

批处理作业调度问题要求确定这n个作业的最优处理顺序，使得从第1个作业在机器1上处理开始，到最后一个作业在机器3上处理结束所需的时间最少。

实例：设J={J1, J2, J3, J4}是4个待处理的作业，需要的处理时间如下所示。

若处理顺序为(J2, J3, J1, J4)，则从作业2在机器1处理开始到作业4在机器3处理完成的调度方案如下：

分析：

解向量：X=(x1, x2, ..., xn)——排列树

约束条件：显式：xi=J1, J2, ..., Jn

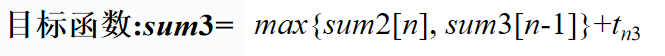
下限界函数：设M是已安排好的作业集合，M

{1, 2, ..., n}, |M|=k。现在要处理作业k+1，有：

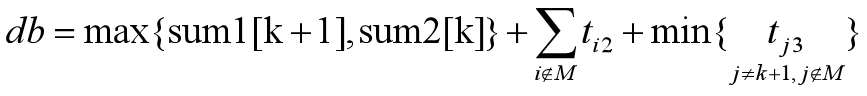
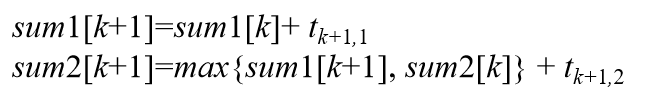
单源最短路径问题

给定一个带权有向图G=（V，E），其中每条边的权是一个正整数。 另外，还给定V中的一个顶点v，称为源点。计算从源点到其他所有顶点的最短路径长度。这里的长度是指路上各边权之和。

用dist数组存放源点v出发的最短路径长度，dist[i]表示源点v到顶点i的最短路径长度，初始时所有dist[i]值为∞。 用prev数组存放最短路径，prev[i]表示源点v到顶点i的最短路径中顶点i的前驱顶点。

1.队列式（FIFO）分支限界法

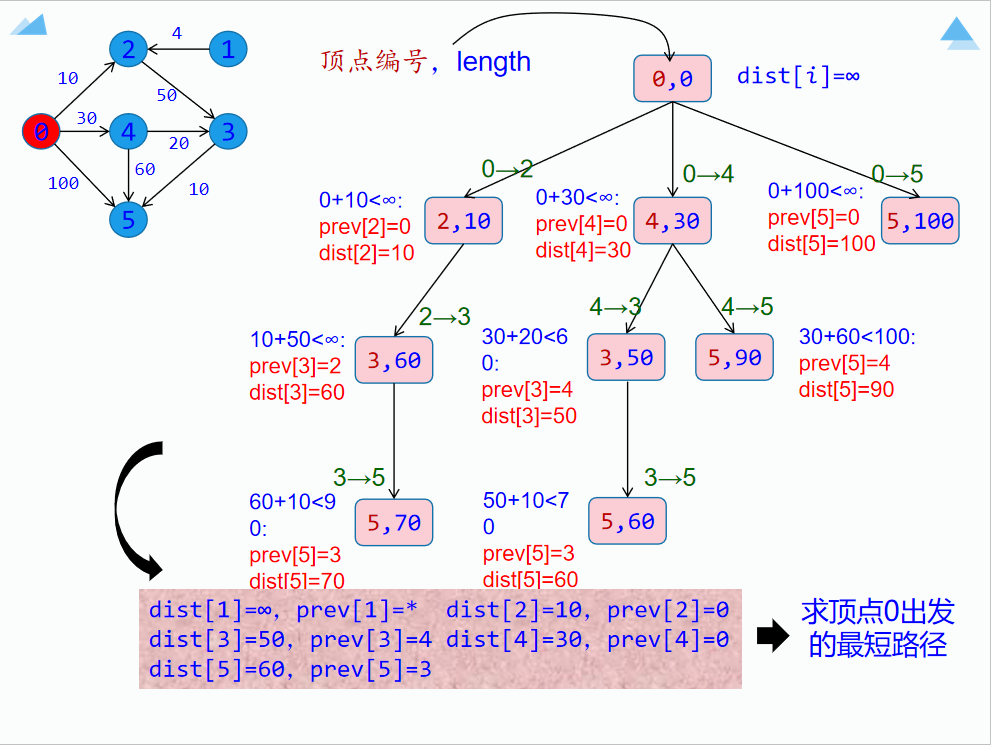
2.优先队列分支限界法

以dist[]作为优先级，dist[]越小优先级越高

完成所有结点遍历就停

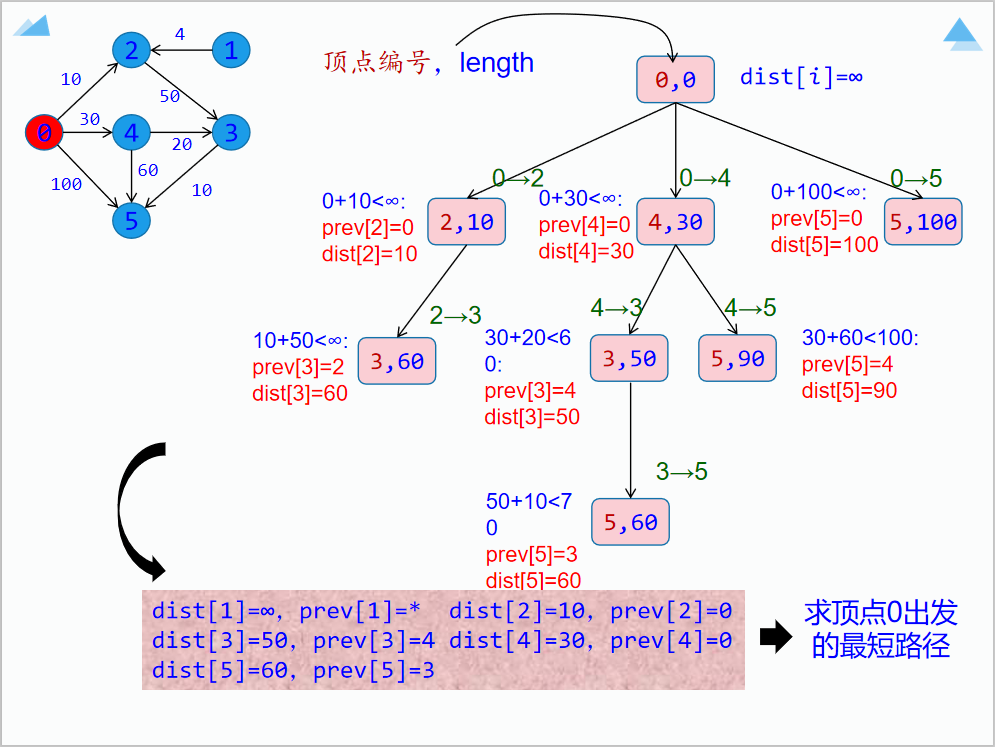
任务分配问题

有n（n≥1）个任务需要分配给n个人执行，每个任务只能分配给一个人，每个人只能执行一个任务。 第i个人执行第j个任务的成本是c[i][j]（1≤i，j≤n）。求出总成本最小的分配方案。

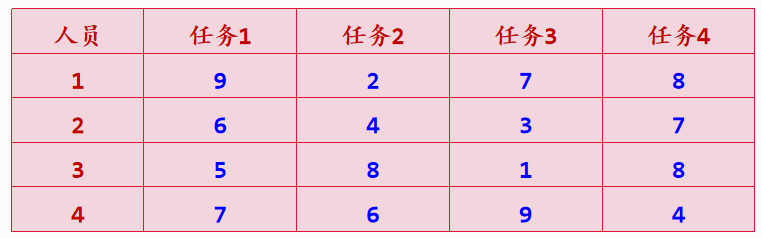
这里采用优先队列式分枝限界法求解。

任务和人员的编号均为1～n，解空间每一层对应一个人员的分配。

根结点对应人员0（虚结点），依次为人员1、2、…、n分配任务。

叶子结点对应人员n。

解向量为x：x[i]表示人员i分配任务编号。初始时所有元素值为0，表示没有分配。

临时标识数组worker：worker[i]=true表示任务i已经分配。初始时所有元素值为false，表示没有分配。用bestx[MAXN]存放最优分配方案， mincost（初始值为∞）存放最优成本。

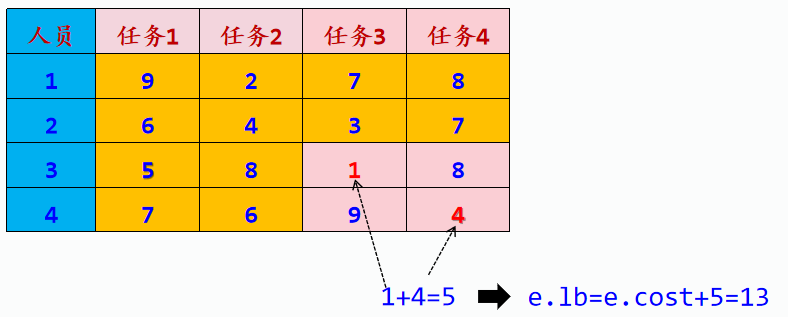
下界限界函数设计

lb为当前结点对应分配方案的成本下界。

例如对于结点e：x[]=[2，1，0，0]，表示第1个人员分配任务2，第2个人员分配任务1，第3、4个人员没有分配任务； 相对应有worker[]=[true,true,false,false]，表示任务1和2已经分配，而任务3、4还没有分配。此时计算结果是：e.cost=c[1][2]+c[2][1]=2+6=8。 下一步最好的情况是在数组c中第3行和第4行中找到非第1、2列（因为任务1、2已经分配）中最小元素和，显然为1+4=5，即其e.lb=e.cost+5=13。

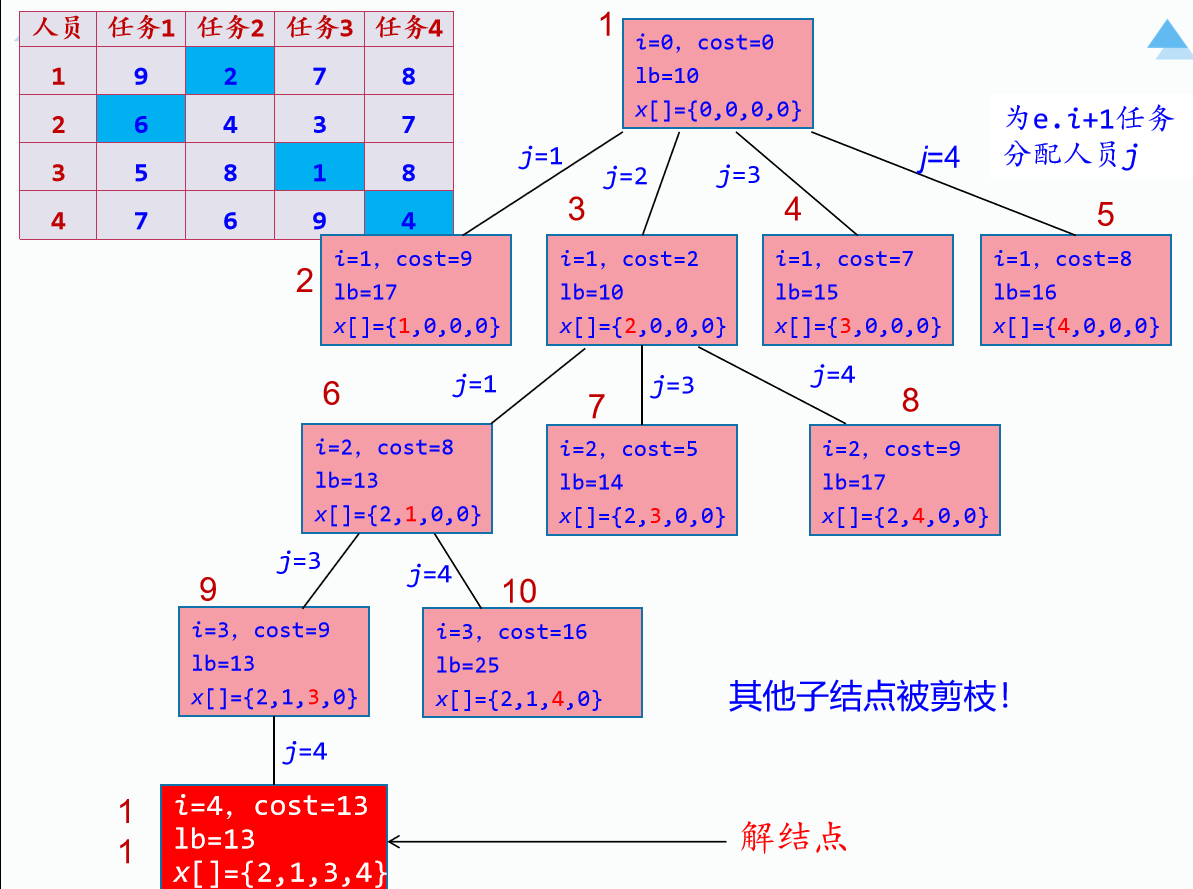
剪枝操作

用bestx[MAXN]存放最优分配方案， mincost（初始值为∞）存放最优成本。

显然一个结点的lb>mincost，则不可能从其子结点中找到最优解，进行剪枝。仅仅扩展lb≤mincost的结点