FFT加窗和频谱泄露

所谓加窗，目的就是针对非整周期采样得到的非自窗信号（self-windowing signal），缓解其频谱分析结果中的能量泄漏现象（注意是“缓解”，而不是“避免”或“消除”）。所谓信号整周期采样（蓝色）和非整周期采样（红色），如图1所示。

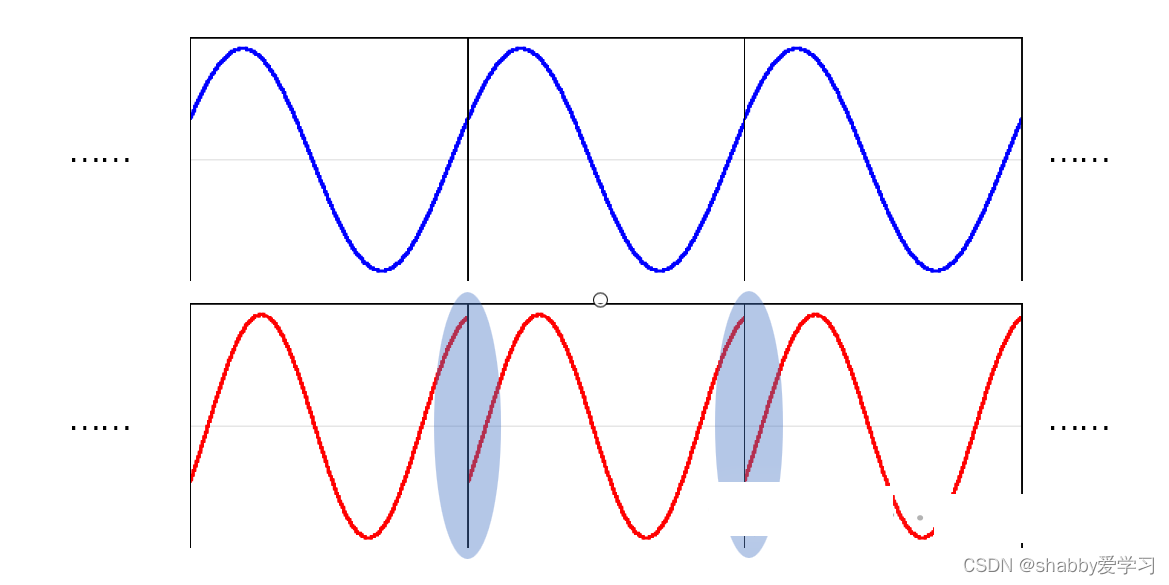
①：由于非整周期截断，对信号周期拓延时，在首尾位置，会出现人为的信号不连续（图1阴影部分），进而造成虚假的高频成分。在FFT分析结果中，这些高频成分会混叠到分析带宽内，使得真实频率处的能量被分散，就是所谓能量泄漏现象；

②：非整周期截断，那么FFT频率分辨率所决定的谱线，就与信号的真实频率不能完全对应了，所以就会造成能量被分散到周边频率。举例来说，信号真实频率为1.5Hz，如果非整周期截断，每次FFT只取1s的样，频率分辨率Δf =1Hz，那么1.5Hz信号成分就无法直接体现出来，而是会被分散到1Hz、2Hz以及周边的谱线上。

下面，我们尝试从信号处理本身的过程，来说一下所谓能量泄漏到底是怎么发生的。：傅里叶变换和FFT，这是两个不同的概念。傅里叶变换

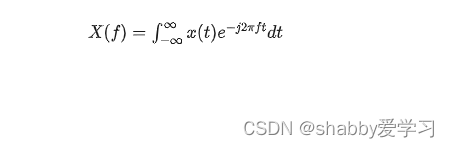
是对连续时间信号x(t)进行积分，得到频域的连续函数X(f)。而FFT是DFT（离散傅里叶变换）的一种快速算法实现，

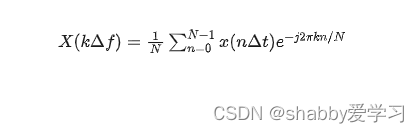
N为采样点数，Δt为采样时间间隔，Δf为频率分辨率。因此FFT是基于时域离散采样点数据x(nΔt)，计算出频域离散函数X(kΔf)的过程。FFT是对连续傅里叶变换得到频域连续函数，在频域进行离散采样，所得到的一个近似的分析结果。
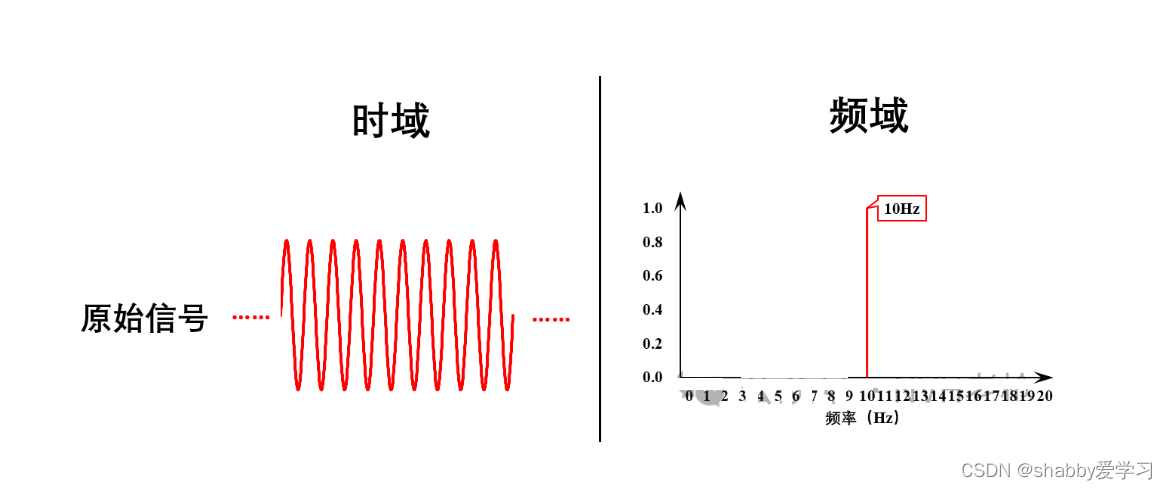
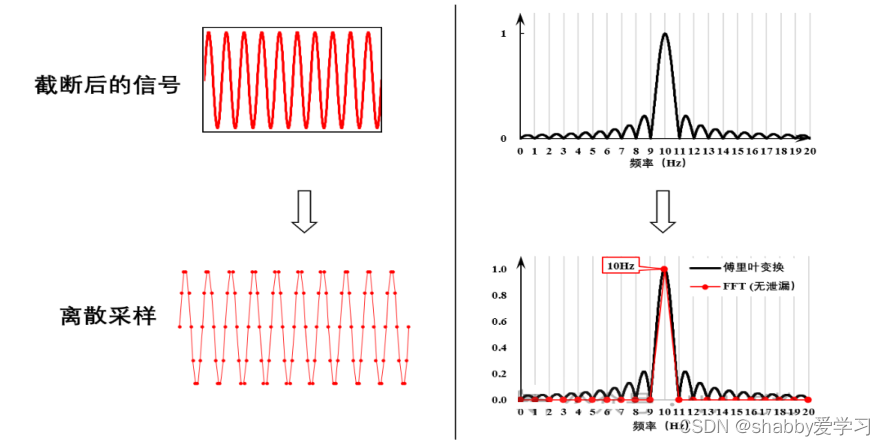
先来看看整周期截断的情况，我们以对一个频率为10Hz，幅值为1的正弦信号FFT分析为例。
1）原始信号原本是一个时间上从－∞变化到＋∞的周期信号，对应的频谱只在10Hz 有能量。

2）我们在进行FFT之前，需要截取一段信号（比如对应1Hz频率分辨率，我们截取1s的数据）。这个数据截取的过程，相当于给原始信号乘一个矩形波，这个矩形波函数，在截取信号的1s时间内，函数值为1，在这截取时间段之外函数值为0。这个截取过程，就像是我们透过一扇窗户去观察信号，所以我们把这个矩形波函数称之为矩形窗函数。

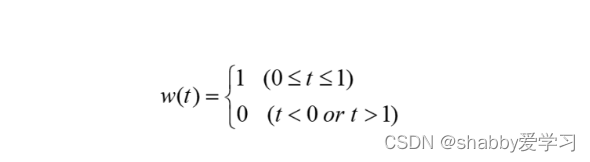
对这个时长1s的矩形窗函数进行傅里叶变换，可以很容易得到其在频域的函数表示。这里引出一个 sinc 函数，sinc(x) = sinx/x，当x = 0时，sinc(x) 函数取极限值为1。

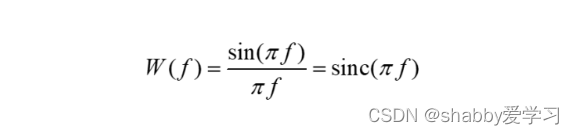
下图中，左图为矩形窗的时域波形，右图是其双边傅里叶变换结果的幅频图。可以看到频谱结果中有一个宽度为2Hz的主瓣，主瓣旁边存在很多旁瓣。

下面将矩形窗函数作用到原始信号上，也就是把矩形窗的时域信号和原始时域信号相乘，完成信号的截取，两个信号在时域相乘，对应频域就是两个信号进行卷积（*）运算。所以截断后信号的傅里叶变换结果中，也出现了旁瓣。

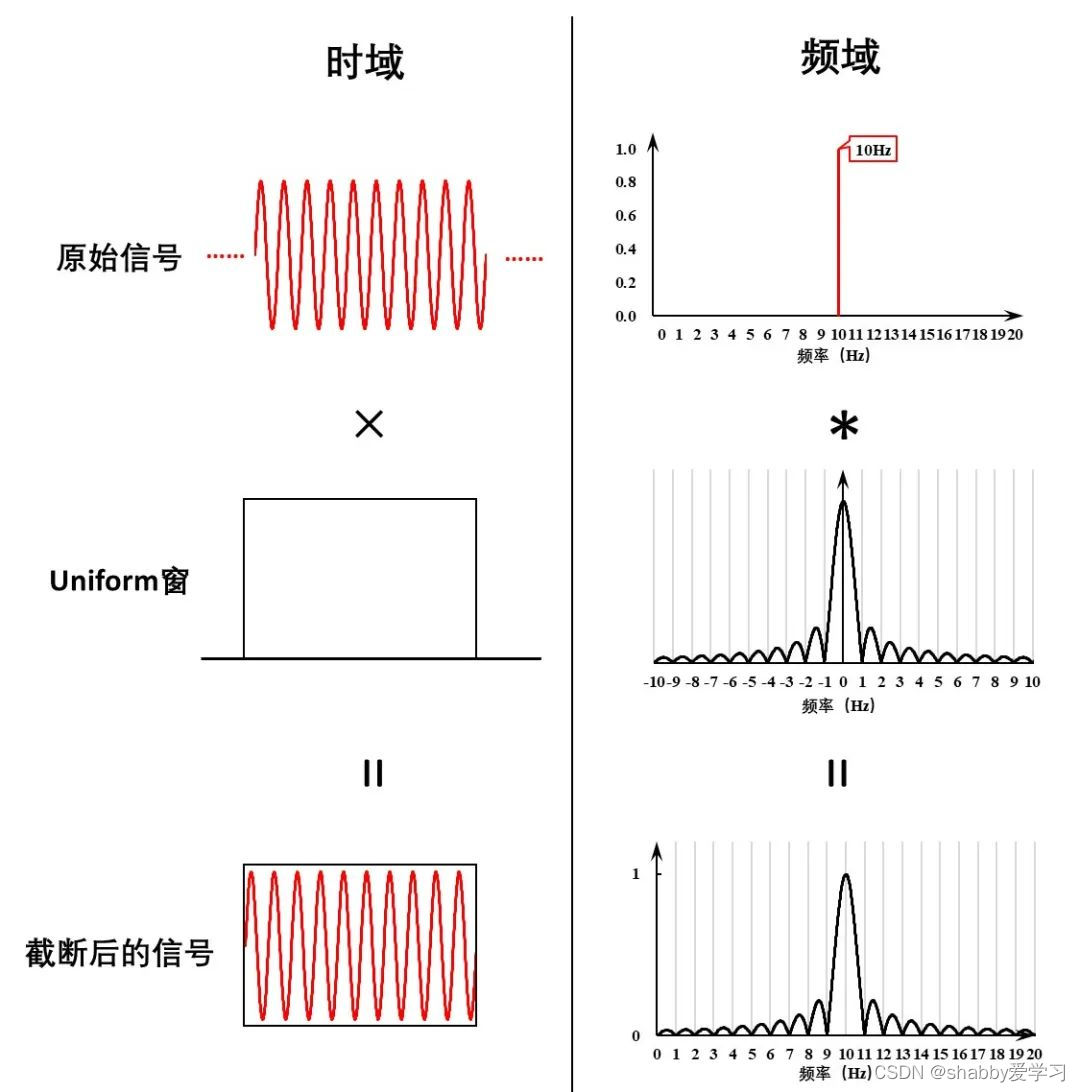
4）最后对截出的信号，分别在时域和频域进行离散采样。时域离散采样大家都很熟悉，那么频域采样，就是对截出信号的傅里叶变换结果，根据1s数据所对应的1Hz的频率分辨率，进行频域的离散采样。（相信大家都知道为什么1s对应1Hz频率分辨率，FFT/DFT中二者互为倒数）此时10Hz正弦信号的能量完全集中在10Hz的谱线上，在所有其他谱线上的结果均为0，分析结果与原始周期信号的频谱完全一致，不存在任何能量的泄漏。

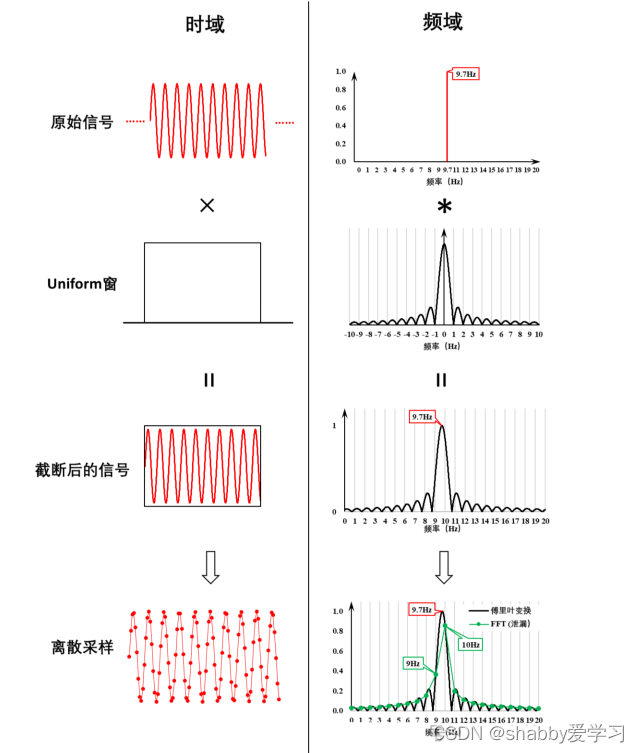
下面看看非等周期截断的情况。对信号频率为9.7Hz的正弦信号，仍然采集1s时间信号。如图中的原始信号时域波形所示，周期拓延后，信号首尾连接处显然会不连续。

分析的过程与上面一样，区别主要在于最后一步的离散采样。对应1Hz分辨率所决定的谱线，依旧从傅里叶分析结果中离散取样，此时所表现出来的结果是，信号的真实频率（9.7Hz）无法对应任何一根谱线，所以信号的能量就被分散到了周边的各条谱线上了。其中与9.7Hz最接近的10Hz谱线上的幅值最大，为0.86。如果以10Hz的这个最大值作为参考，与原周期正弦信号的幅值相比，结果出现了14%的误差。此外，在主瓣另一根谱线上（9Hz），也存在一个比较明显的分量。

能量泄漏的改善：
Hann窗（时长1s）的时域函数为：

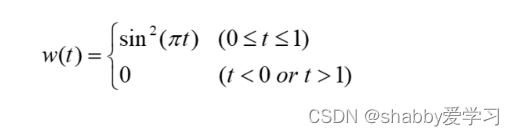
通过傅里叶变换，可计算出其频域的函数表达：

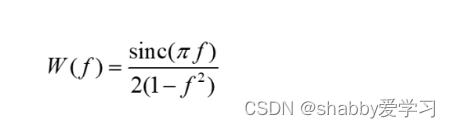
Hann窗的时频特性如图所示。可以看到相比较矩形窗，Hann窗的主瓣要宽一倍，而旁瓣的幅值要小很多。所以，从截断后信号的傅里叶变换频谱中可以看到，相比较矩形窗而言，信号能量从主瓣泄漏到旁瓣的现象，得到了明显的抑制和改善。

对加窗截断后的信号，分别在时域和频域离散采样，并对FFT分析结果进行窗函数幅值修正（所谓窗函数修正是怎么回事，有机会在以后的文章再说），可以看到现在10Hz谱线上的结果为0.94，误差从矩形窗的14% 降低到了6%。但也注意到，在主瓣上的其他3根谱线（8Hz，9Hz，11Hz）上，也出现不小的分量。

因此，当我们使用Hann窗进行频谱分析时，如果在某个频率附近，相邻的3-4根谱线都有一定的分量，并不总是代表这里存在着3~4个不同的频率成分，而很可能是由于信号非等周期截断所造成的能量分散。

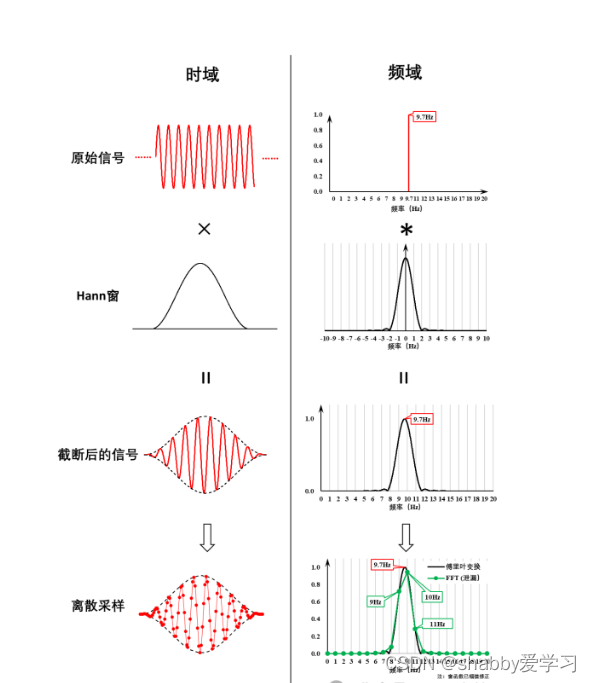
如果是非等周期采样，FFT分析结果就将无法准确复现原始周期信号的频谱特征，表现为真实频率处的信号能量，被泄漏到了窗函数所引起的主瓣及周边旁瓣的各条谱线上，即所谓能量泄漏现象。