【算法】一维、二维前缀和 解决算法题(C++)
发布时间:2024年01月02日
文章目录
1. 前缀和算法 介绍
前缀和算法 用于高效地计算 数组或序列 中某个区间内元素的和。
前缀和数组是一个辅助数组,其每个元素存储原始数组从开头到当前位置的元素和。通过提前计算前缀和数组,可以在O(1)的时间复杂度内快速计算出任意区间内的元素和。
2. 一维前缀和 模板引入
DP34【模板】前缀和

这道题目帮助我们 理解前缀和模板 和 使用前缀和数组 :
思路
-
题意分析:题目要求我们返回 数组中l~r范围内所有元素的和
-
我们引出前缀和数组dp的使用:

-
解法:前缀和数组
- 我们首先通过循环
dp[i] = dp[i-1] + arr[i]进行dp数组的初始化(预处理) - 再根据找到的规律,l~r的范围和即为
dp[r]-dp[l-1]
- 我们首先通过循环
代码
int main() {
int n = 0, q = 0;
cin >> n >> q;
vector<int> arr(n+1); // 下标从1开始,数组大小为n+1
// 写入数组
for(int i = 1; i <= n; ++i) cin >> arr[i];
// 预处理前缀和数组
vector<long long> dp(n+1); // long long 防止溢出
for(int i = 1; i <= n; ++i) dp[i] = dp[i-1] + arr[i];
// 使用前缀和数组
while(q--)
{
int l, r;
cin >> l >> r;
cout << dp[r] - dp[l-1] << endl;
}
return 0;
}
3. 利用一维前缀和 解题
724.寻找数组的中心下标

思路
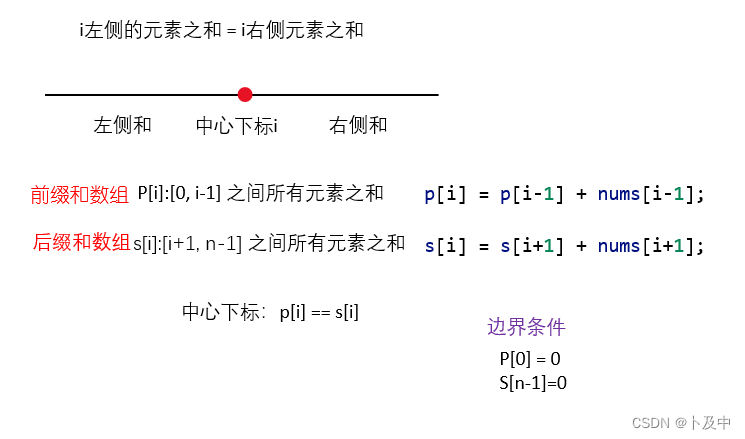
- 题意分析:要求我们找到数组的中心下标,中心下标满足:左侧元素和==右侧元素和
- 解法:前缀和数组 + 后缀和数组
- 预处理前缀和 / 后缀和数组
p[i] = p[i-1] + nums[i-1];s[i] = s[i+1] + nums[i+1];
- 遍历数组:找到满足条件的中心下标(p[i] == s[i])
- 细节注意:关于创建两数组时,循环条件从哪到哪。
- 预处理前缀和 / 后缀和数组
代码
int pivotIndex(vector<int>& nums) {
int n = nums.size();
// 预处理前缀和数组
vector<int> p(n); // P[i]:[0, i-1] 之间所有元素之和;
for(int i = 1; i < n; ++i) // p[0] == 0 s[n-1] == 0]
p[i] = p[i-1] + nums[i-1];
// 预处理后缀和数组
vector<int> s(n); // s[i]:[i+1, n-1] 之间所有元素之和
for(int i = n - 2; i >= 0; i--)
s[i] = s[i+1] + nums[i+1];
// 通过前缀和/后缀和数组找到中心下标
int i;
for(i = 0; i <= n - 1; ++i)
{
if(p[i] == s[i])
return i;
}
return -1;
}
238.除自身以外数组的乘积

思路
- 题意分析:返回数组answer,answer[i]为nums中除去自身的其余元素乘积。
- 解法:前缀积数组 + 后缀积数组
- 我们知道:不论是前缀和还是前缀积数组,p[i]的值代表0~i-1位置的和/积,不包括其自身。
- 则当我们求出数组的前缀积和后缀积后,answer[i] 即为 p[i] * s[i]。

代码
vector<int> productExceptSelf(vector<int>& nums) {
int n = nums.size();
vector<int> p(n), s(n);
p[0] = s[n-1] = 1; // 边界条件
// 构建前缀积数组
for(int i = 1; i <= n - 1; ++i)
p[i] = p[i-1] * nums[i-1];
// 构建后缀积数组
for(int i = n-2; i >= 0; --i)
s[i] = s[i+1] * nums[i+1];
vector<int> answer(n);
for(int i = 0; i < n; ++i)
answer[i] = p[i] * s[i];
return answer;
}
560.和为K的子数组
思路
- 题意分析:题目要求找到和为k的子数组的个数。
- 解法一:暴力枚举
- 一道题如果没有思路,首先可以想暴力解法
- 即:用两个循环遍历所有子数组,找到和为k的
- 缺点:时间开销大,时间复杂度O(n^2)
- 为什么不能使用双指针(滑动窗口)?
- 我们知道,双指针适合解决子数组问题,但其是解决连续子数组,这道题满足要求的子数组不一定连续。且数组中存在负数,也不能利用单调性使用滑动窗口。
- 解法二:前缀和 + 哈希表
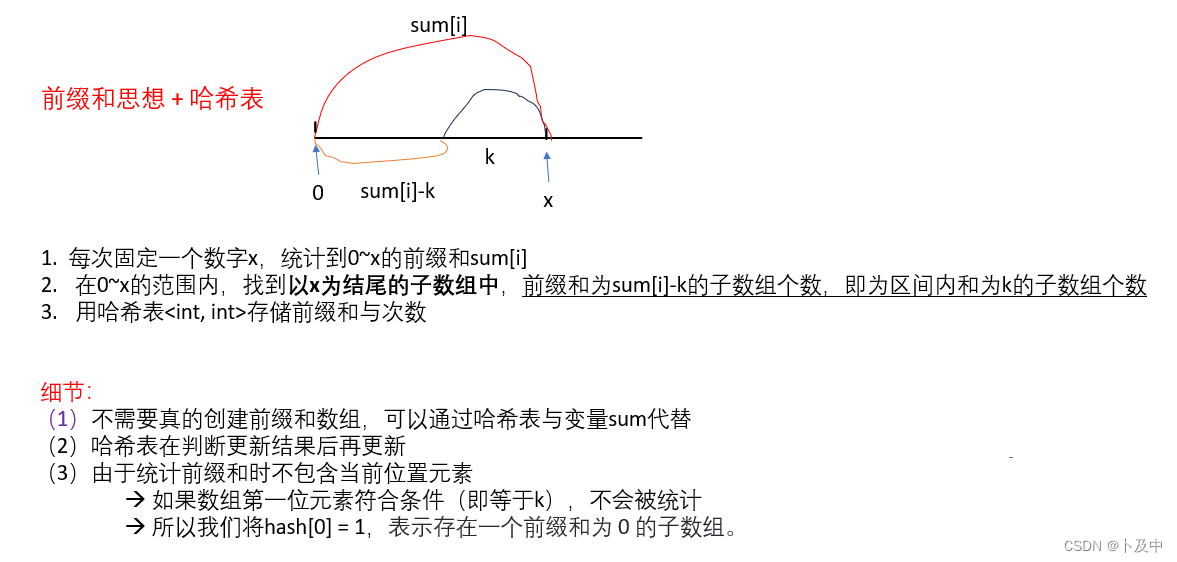
- 如上图所示
代码
int subarraySum(vector<int>& nums, int k) {
int sum = 0, count = 0; // sum存储前缀和
unordered_map<int, int> hash;
hash[0] = 1; // 特殊情况:当子数组的第一个元素就满足条件的情况时
for(int x : nums)
{
sum += x;
// 以x为结尾的子数组,值为sum-k,则存在满足和为k的子数组
if(hash.count(sum-k)) count += hash[sum-k];
hash[sum]++;
}
return count;
}
974.和可被K整除的子数组

思路
- 题意分析:此题和前一题很像,只是从求和为k的子数组变成求和可被k整除的子数组的个数
- 解法:前缀和 + 哈希表
- 思路与之前一致,我们每次在更新前缀和sum后,更新余数r,如果哈希表中存在则更新结果
- 细节注意:同理为了防止前缀和为0的子数组满足条件,则将hash[0%k](就是0)定为1
代码
int subarraysDivByK(vector<int>& nums, int k) {
// C++,java 中负数%正数=负数
// 为了使余数满足题目条件,余数计算为(sum % k + k) % k
int sum = 0, count = 0;
unordered_map<int, int> hash;
hash[0 % k] = 1; // hash[0] = 1;
for(int x : nums)
{
sum += x;
int r = (sum % k + k) % k;
if(hash.count(r)) count += hash[r];
hash[r]++;
}
return count;
}
525.连续数组

思路
- 题意分析:要求找到有相同数量0和1的最长子数组
- 这道题要求我们找到最长连续子数组,但是没有直接单调性,不能使用滑动窗口解题
- 将数组中的1全部改为0,题目就转化为了:找和为0的连续最长子数组
- 相当于将和为K的子数组改为了和为0的子数组 ,但需要注意的是,这道题要求的是最长子数组的长度:所以我们用哈希表分别存储前缀和+下标
- 解法:前缀和 + 哈希表
- 我们每次将前缀和加入到数组中,如果已经存在,则根据长度更新结果
- 否则将当前下标与前缀和加入到hash中
- 细节注意:因为我们计算长度是用:下标i-hash[sum]
- 如果首位就是满足条件的,此时长度应为1
- 即i - hash[0] = 1,此时i为0,为了保证特殊情况,我们将hash[0]设为-1
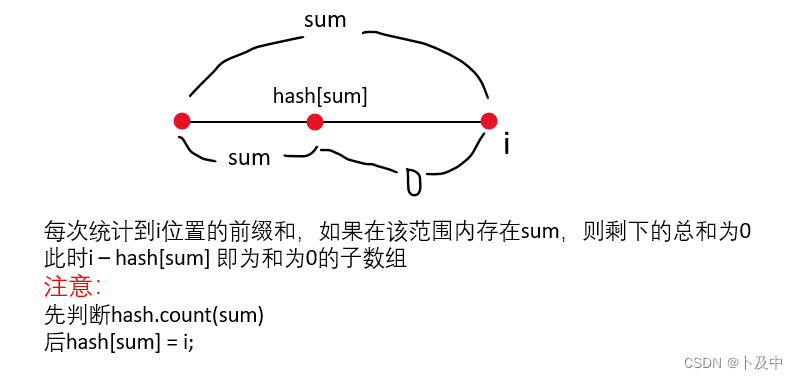
代码
int findMaxLength(vector<int>& nums) {
int sum = 0, ret = 0;
// 将数组中的0改为-1,题目可以演化为:求和为0的子数组
//for(int &x : nums) x = 0 ? -1 : x;
unordered_map<int, int> hash; // 哈希表存放前缀和以及下标
hash[0] = -1;
for(int i = 0; i < nums.size(); ++i){
sum += nums[i] == 0 ? -1 : 1; // 更新前缀和
if(hash.count(sum)) // 前缀和sum存在 则更新ret(hash[sum] 为前缀和尾部下标, i-hash[sum] 为 连续数组长度)
ret = max(ret, i - hash[sum]);
else
hash[sum] = i;
}
return ret;
}
二维前缀和 模板
1314.矩阵区域和

思路
-
题意分析:题目要求返回answer矩阵,矩阵每一位元素可以理解为是以mat的每一位为中心,向上下左右分别扩展k个单位的元素总和。
-
解法:二维前缀和
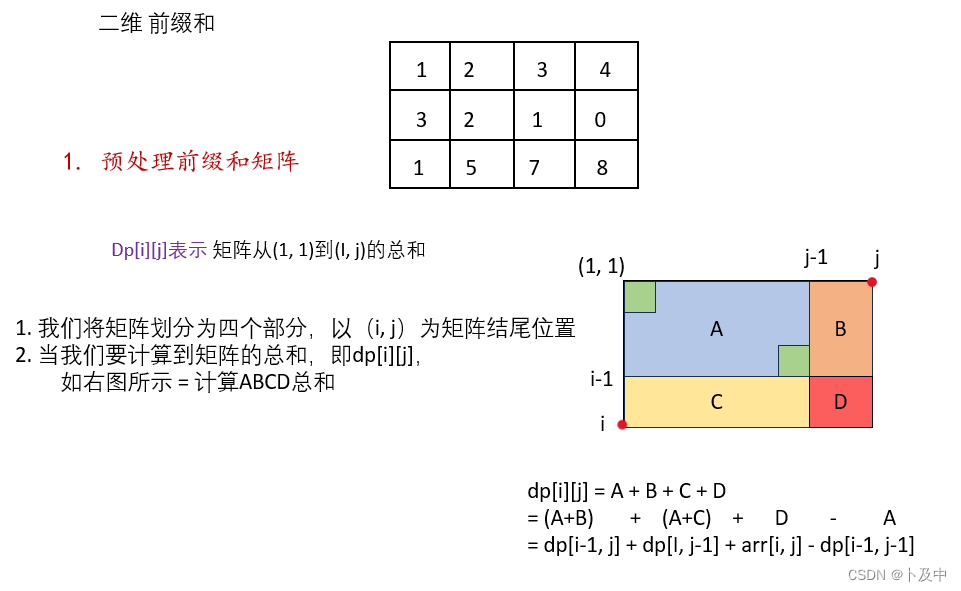
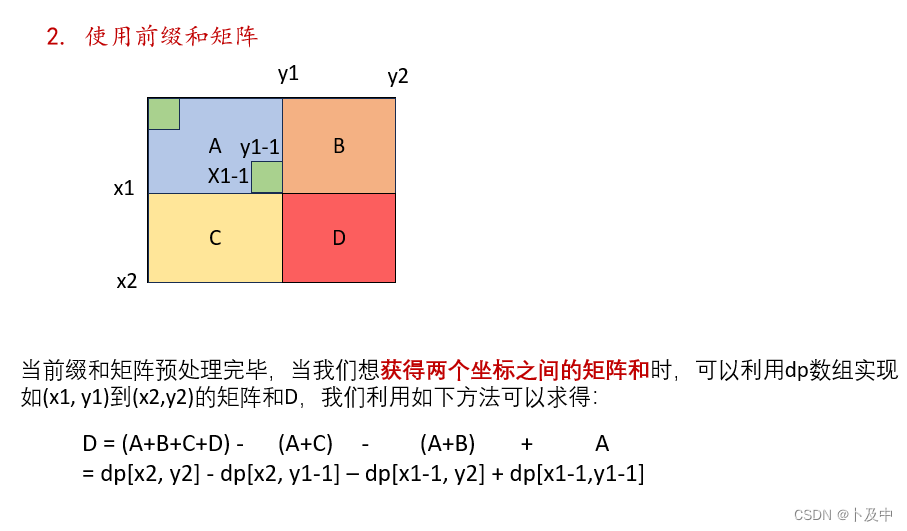
- 根据上面的图,我们首先用两层循环预处理前缀和矩阵
- 随后使用前缀和矩阵:只需要根据当前的(i, j)下标找到其向四周扩散的矩阵的左上和右下的坐标即可
- 根据求得的(x1, y1) (x2, y2) 以及我们算出的公式计算结果
-
需要注意的是,最好不要死记模板公式,理解了过程,做题的时候可以模拟,自然会想出来过程
代码
vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
int m = mat.size(), n = mat[0].size();
// 预处理前缀和矩阵
vector<vector<int>> dp(m+1, vector<int>(n+1)); // 扩充一行一列:对应下标
for(int i = 1; i <= m; ++i)
for(int j = 1; j <= n; ++j)
dp[i][j] = dp[i-1][j] + dp[i][j-1] + mat[i-1][j-1] - dp[i-1][j-1];
// 使用前缀和矩阵 构建answer
vector<vector<int>> answer(m, vector<int>(n));
for(int i = 0; i < m; ++i)
{
for(int j = 0; j < n; ++j)
{
// answer[0][0] 对应 dp[1][1],把坐标+1
int x1 = max(i-k, 0) + 1, y1= max(j-k, 0) + 1;
int x2 = min(i+k, m-1) + 1, y2 = min(j+k, n-1) + 1;
answer[i][j] = dp[x2][y2] - dp[x2][y1-1] - dp[x1-1][y2] + dp[x1-1][y1-1];
}
}
return answer;
}
文章来源:https://blog.csdn.net/Dreaming_TI/article/details/135248679
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【知识点随笔分析 | 第六篇】HTTP/1.1,HTTP/2和HTTP/3的区别
- 宝强前经纪人宋喆出狱后首露面;美团外卖平台KeeTa;电视开机率跌至30%;朝军发射200多枚炮弹
- L1-071 前世档案(Java)
- 速盾网络:cdn数量对网站访问速度的影响
- 短视频赋能:TikTok对用户自我表达的推动
- 如何本地搭建开源分布式任务调度系统DolphinScheduler并远程访问
- 策略模式在工作中的运用
- 10-高并发-应用级缓存
- 为什么企业容易陷入“自嗨式营销”,媒介盒子分析
- 【数据结构】图