并查集（C++）

一、并查集的原理

并查集的两个功能：

• 合并：合并两个不想联系的元素
• 查询：判断两个元素是否在同一个组内

主要解决的是元素分组的问题。

---

例如：某班级要创建三个兴趣小组，分别是象棋、游泳、篮球。
班级总人数10人，现在需要不10人分别添加到三个兴趣小组中，每个人只能参加一个兴趣小组。

象棋小组：{2，4，6，7}
游泳小组：{0，1，5，8}
篮球小组：{3，9}

这里就可以使用到并查集。

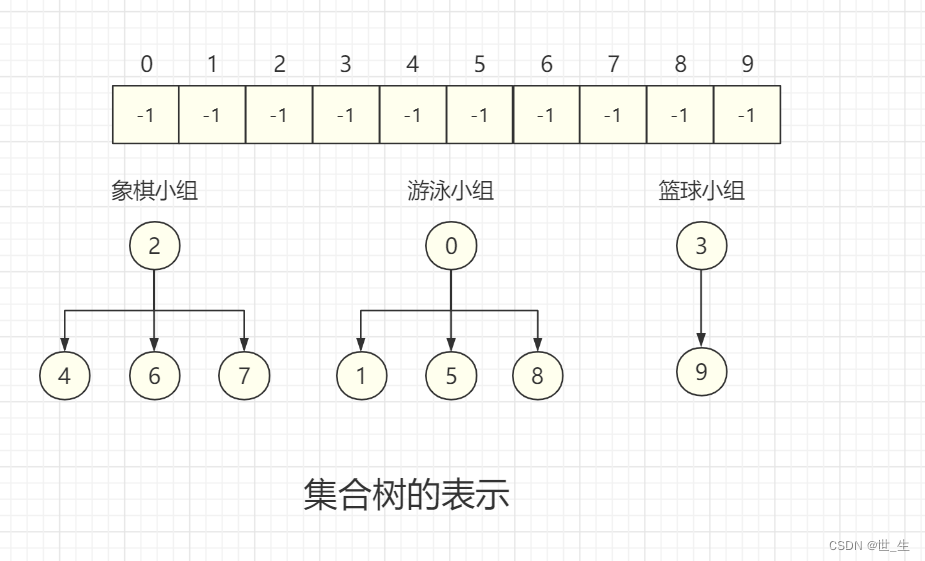
在数组中的表示：

1.数组的下标对应集合中元素的编号（映射关系）
2.数组中如果为负数，负号代表根，数字代表该集合中元素个数
3.数组中如果为非负数，代表该元素双亲在数组中的下标

---

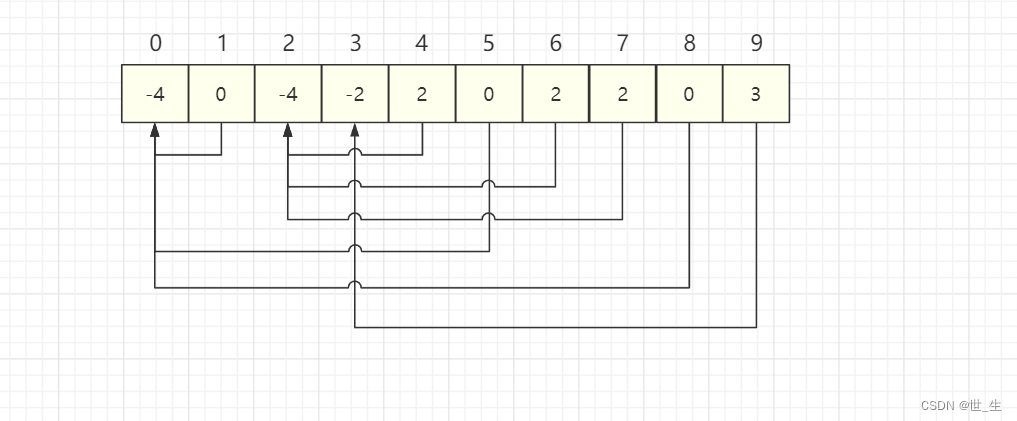
例如：由于篮球小组人比较少，某班级决定解散，成员合并到游泳小组。

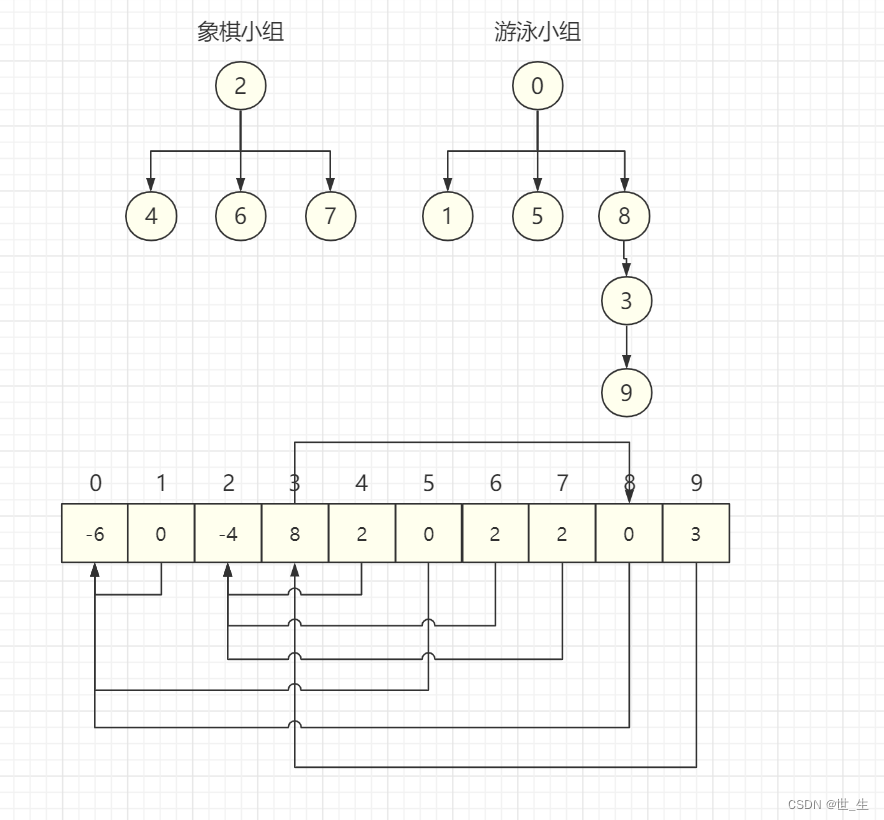
1. 数组0下标的数据变为-6
2. 数组3下标的数据变为8

二、并查集的实现

代码实现：

1.使用vector容器
2.实现合并功能（一个节点只能附属一个根节点）
3.实现查询功能（判断两个节点的根节点是否相同）

#pragma once
#include<iostream>
#include<vector>
using namespace std;
template<class T>
class UnionFindSet {
public:
	UnionFindSet(const size_t n)
		:UFS(n,-1)
	{}

	//合并查集
	void UnionSet(const int x,const int y)
	{
		int root1 = FindRoot(x);
		int root2 = FindRoot(y);

		if (root1 != root2)
		{
			//合并：控制数量少的往控制数量大的合并（合并意味着层数多了一层）
			if (abs(UFS[root1]) < abs(UFS[root2]))
				swap(root1, root2);

			UFS[root1] += UFS[root2];
			UFS[root2] = root1;
		}
	}
	
	//寻找节点的根
	int FindRoot(int index)
	{
		int temp = index;
		while (UFS[index] >= 0)
		{
			index = UFS[index];
		}

		//子树全部去直接连接根（路径压缩）
		while (UFS[temp] >= 0)
		{
			int next = UFS[temp];
			UFS[temp] = index;
			temp = next;
		}
		return index;
	}	

	//计数森林的个数
	int CountSet()
	{
		int count = 0;
		for (auto n: UFS)
		{
			if (n < 0)
				++count;
		}
		return count;
	}
private:
	vector<T> UFS;
};

路径压缩

1、数量少的森林往数量多的森林合并。（在合并的时候进行优化）
数量多的森林往往代表的查询频率多，如果往数量少的森林上合并，就会使原有的层数+1，提高了查询的成本。
2、子节点全部直接和根节点联系，降低森林的层数。（在查询的时候进行优化）

三、并查集的应用

题1：省份问题
题2：等式方程的可满足性

题1思路：

• 矩阵的横、纵坐标代表这省份之间的联系，1代表联系需要合并，0代表不联系不需要合并。
• 最后计算森林的数量

题2思路：

• 建立字母和数组下标映射关系
• 合并==的两个字母
• 最后查询!=的两个字母是否有相同的根，有相同的根则false

结尾

不定期更新，给小编点点赞，为小编加加油，点赞?收藏不迷路噢~??

下一篇：讲解图。