二分查找及其复杂的计算

（一）二分查找及其实现

二分查找，也称为折半查找，是一种高效的搜索算法，用于在有序数组（或有序列表）中查找特定元素的位置。

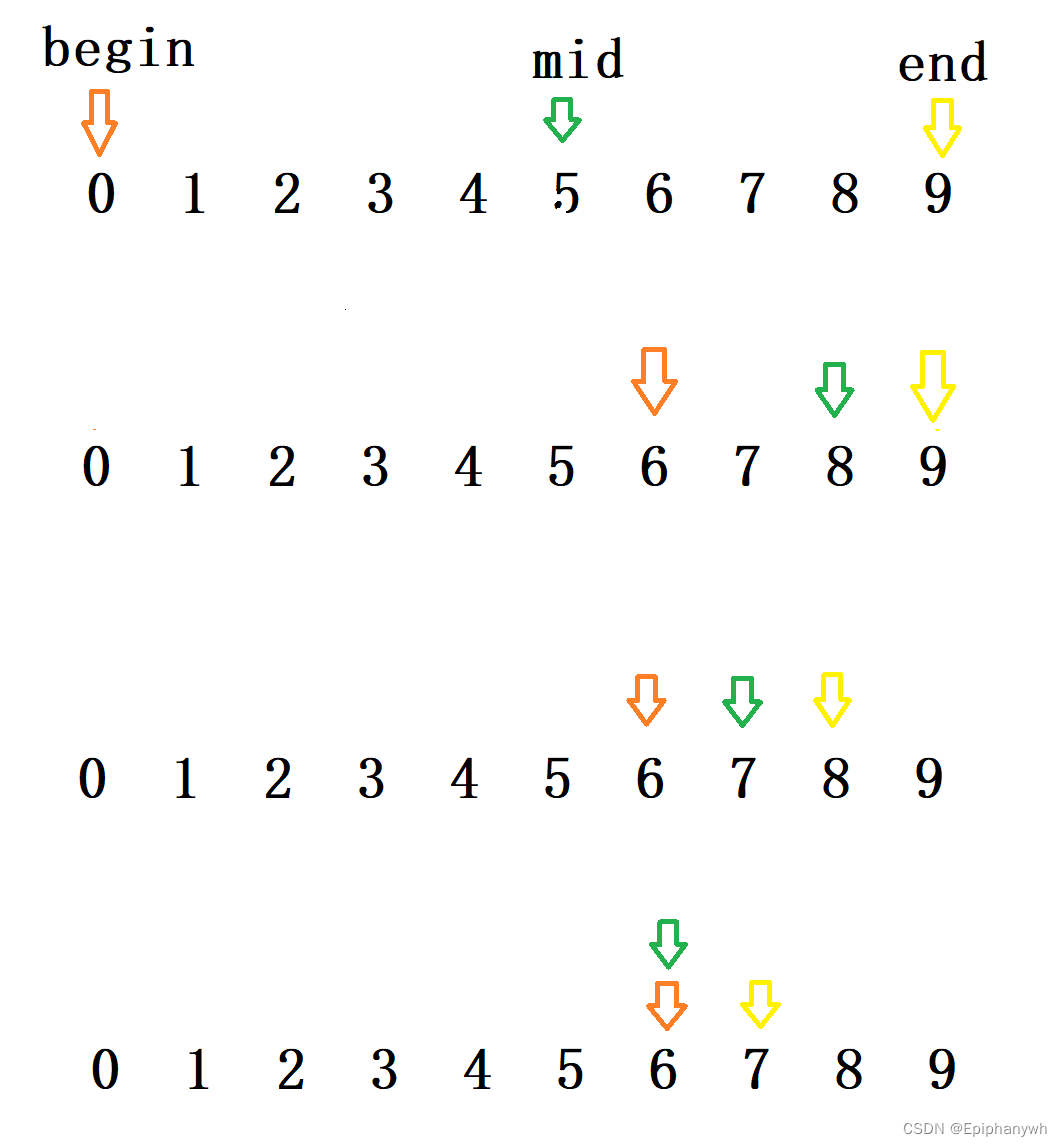
二分查找的基本思想是将待查找的区间不断地二分，然后确定目标元素位于左半部分还是右半部分，从而缩小查找范围。具体步骤如下：

1. 确定初始的查找区间，一般为整个数组或列表。
2. 找到待查找区间的中间位置（mid）。
3. 比较中间位置的元素与目标元素的大小关系：
   • 如果中间位置的元素等于目标元素，直接返回该位置。
   • 如果中间位置的元素大于目标元素，说明目标元素可能位于左半部分，将查找区间缩小为左半部分。
   • 如果中间位置的元素小于目标元素，说明目标元素可能位于右半部分，将查找区间缩小为右半部分。
4. 在新的查找区间上重复步骤2和步骤3，直到找到目标元素或者确定目标元素不存在（即查找区间为空）为止。

二分查找的时间复杂度为O(log n)，其中n表示数组或列表的长度。相比线性查找的O(n)时间复杂度，二分查找的效率更高。但要注意，二分查找要求数组或列表是有序的，否则无法正确进行查找。

需要特别注意的是，二分查找适用于静态查找（即不会频繁插入、删除元素）的情况，并且要求查找的数据结构支持随机访问。对于动态变化的数据集，如链表，二分查找并不适用。

代码如下：

#include <stdio.h>
int BinarySearch(int arr[], int n, int x)
{
	int right = n;
	int left = 0;
	while (left < right)
	{
		int mid = left + ((right - left) >> 1);
		if (arr[mid] > x)
			right = mid;
		else if (arr[mid] < x)
			left = mid + 1;
		else
			return mid;//当arr[mid]==x时，返回下标
	}
	return -1;//没找到返回-1
}
int main()
{
	int arr[10] = { 0,1,2,3,4,5,6,7,8,9 };
	int n = sizeof(arr) / sizeof(arr[0]);
	int ret = BinarySearch(arr, n, 6);
	printf("目标元素的下标是：%d\n", ret);
	return 0;
}

????????

?（二）二分查找的复杂度

想要得到二分查找的复杂度，仅仅看代码是不能得到正确的答案的，要分析代码的逻辑。

查找最多次的情况有两种：第一种是该数列中没有目标数据；第二种是最后一次才找到目标数据（其实就是目标数据在最左面或最右面）。

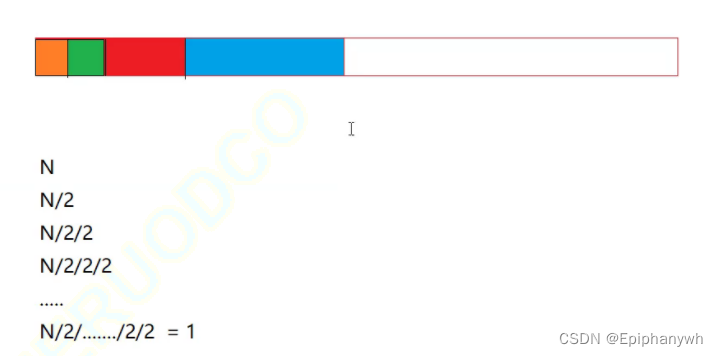
有代码可知，一次得到mid再进行判断,可以排除一半的数据。可以设经过x次求mid和判断，能够找到目标数据。

展开的思想：

找到目标数据，最终得到一个数据，一次排除一半的数据，也就意味着倒数第二次的数据个数（排除前）是最后一次的数据个数的二倍，而倒数第三次的数据个数是倒数第二次数据个数的二倍……

依次类推，直到展开得到第一次二分前的数据个数，而这个数据个数就是所有的数据个数，也即N个。所以有以下等式：

1*2*2*2……*2=N

2^x=N

得到 x = log2n，也即时间复杂度为O（log2n）.

从二分查找的时间复杂度可以看出，二分查找的效率是十分高的，但是使用二分查找算法需要先做好排序的准备工作。

因此，二分查找的时间复杂度为O(log n)，其中n为待查找区间的长度。