Java实现LeetCode447.回旋镖的数量
发布时间:2024年01月10日
题目描述
给定平面上 n 对 互不相同 的点 points ,其中 points[i] = [xi, yi] 。回旋镖 是由点 (i, j, k) 表示的元组 ,其中 i 和 j 之间的距离和 i 和 k 之间的欧式距离相等( 需要考虑元组的顺序 )。
返回平面上所有回旋镖的数量。
思路

首先,看到数据量,判断应该可以暴力+模拟,似乎也没有什么别的好方法。
先开始想的是数据结构是Map<Integer,List<int[][]>>,其中key为点之间的距离distance,val结构是list<int[][]>,放具体两点的坐标。那么经过两层循环后,示例一在map中的数据如下:
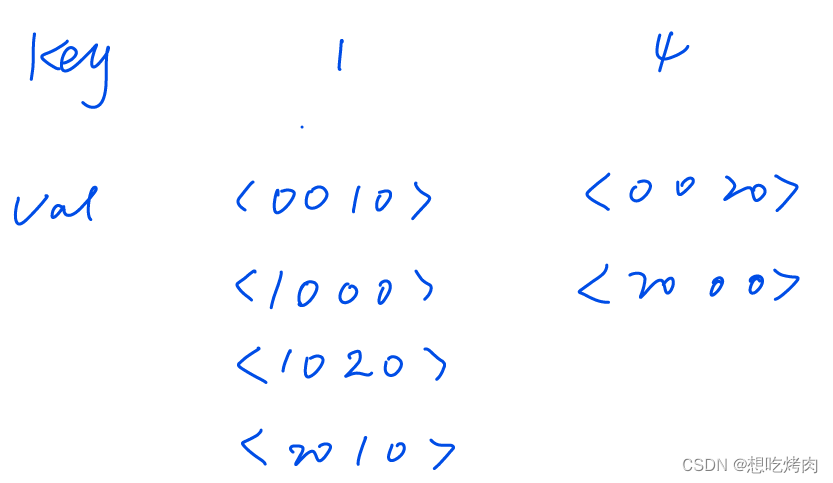
显然,val里存在顺序不同的元组对,还需要对val进行循环判断,遂放弃。
看了题解以后,发现同样是双重循环,但是先将回旋镖的 中间点a 定下来,维护一个map,记录到该中间点距离为某定值的点 b 的数量,进行排列组合后累加。
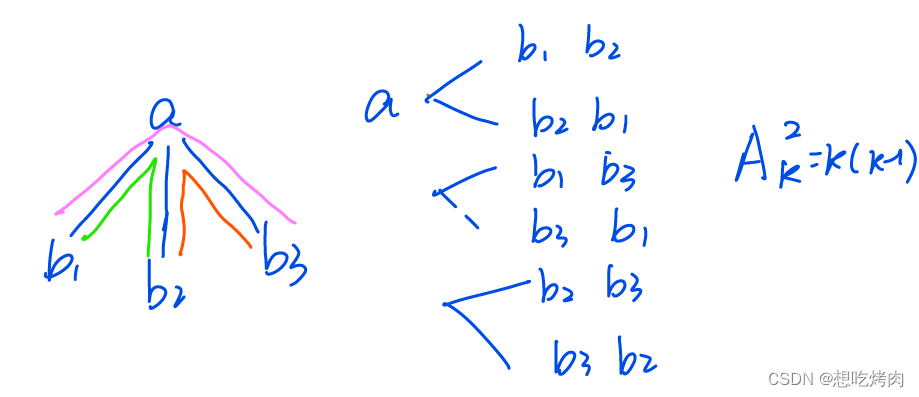
代码
class Solution {
public int numberOfBoomerangs(int[][] points) {
int len = points.length;
int ans = 0;
for( int i = 0 ; i < len ; i++ ){
Map<Integer, Integer> mp = new HashMap();
for( int j = 0 ; j < len ; j++ ){
if( i==j ) continue;
int x = points[i][0] - points[j][0];
int y = points[i][1] - points[j][1];
int dis = x * x + y * y;
mp.put( dis , mp.getOrDefault( dis , 0 ) + 1 );
}
for( int key : mp.keySet() ){
int val = mp.get( key );
ans += ( val*(val-1 ) );
}
}
return ans;
}
}
反思
学习使用map的getOrDefault函数,可以避免if else讨论map中是否存在key
文章来源:https://blog.csdn.net/weixin_43273560/article/details/135450801
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 带你深度理解什么是CRM客户关系管理?
- 一段与VFP共舞的编程岁月
- 对比Numpy的数组和Python列表的求和速度
- 笨蛋学设计模式行为型模式-责任链模式【18】
- java swing UI第三方设计器JFormDesiner和FlatLaf UI
- 小程序商城的优势是什么?
- 基于PHP的医院办公管理系统
- 内存 vs 硬盘:固态硬盘代替内存可以工作吗?
- 【SpringBoot】mybatis基础操作
- 阿里面试:说说Rocketmq推模式、拉模式?