数据结构之排序二叉树
排序二叉树
基本概念
二叉树是一种从上往下的树状结构的数据结构,从根节点开始每个节点最多有两个子节点,左边的为左子节点,右边的为右子节点。
排序二叉树–有顺序,且没有重复元素的二叉树。顺序为:
对每个节点而言:
1)如果左子树不为空,则左子树上的所有节点都小于该节点;
2)如果右子树不为空,则右子树上的所有节点都大于该节点;
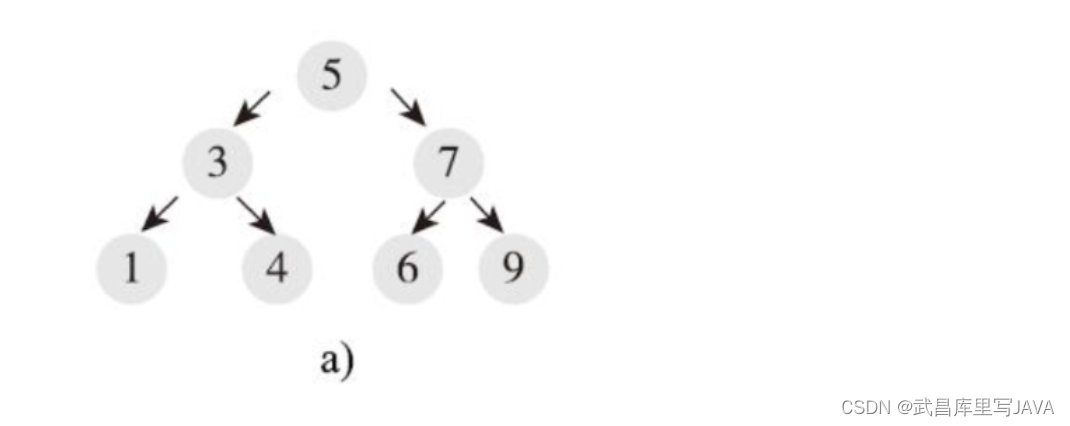
如图,根节点为5,左边的节点都大于5,右边的节点都小于5。
插入操作
首先要从根节点开始往下找到自己要插入的位置(即新节点的父节点);具体流程是:新节点与当前节点比较,如果相同则表示已经存在且不能再重复插入;如果小于当前节点,则到左子树中寻找,如果左子树为空则当前节点为要找的父节点,新节点插入到当前节点的左子树即可;如果大于当前节点,则到右子树中寻找,如果右子树为空则当前节点为要找的父节点,新节点插入到当前节点的右子树即可。
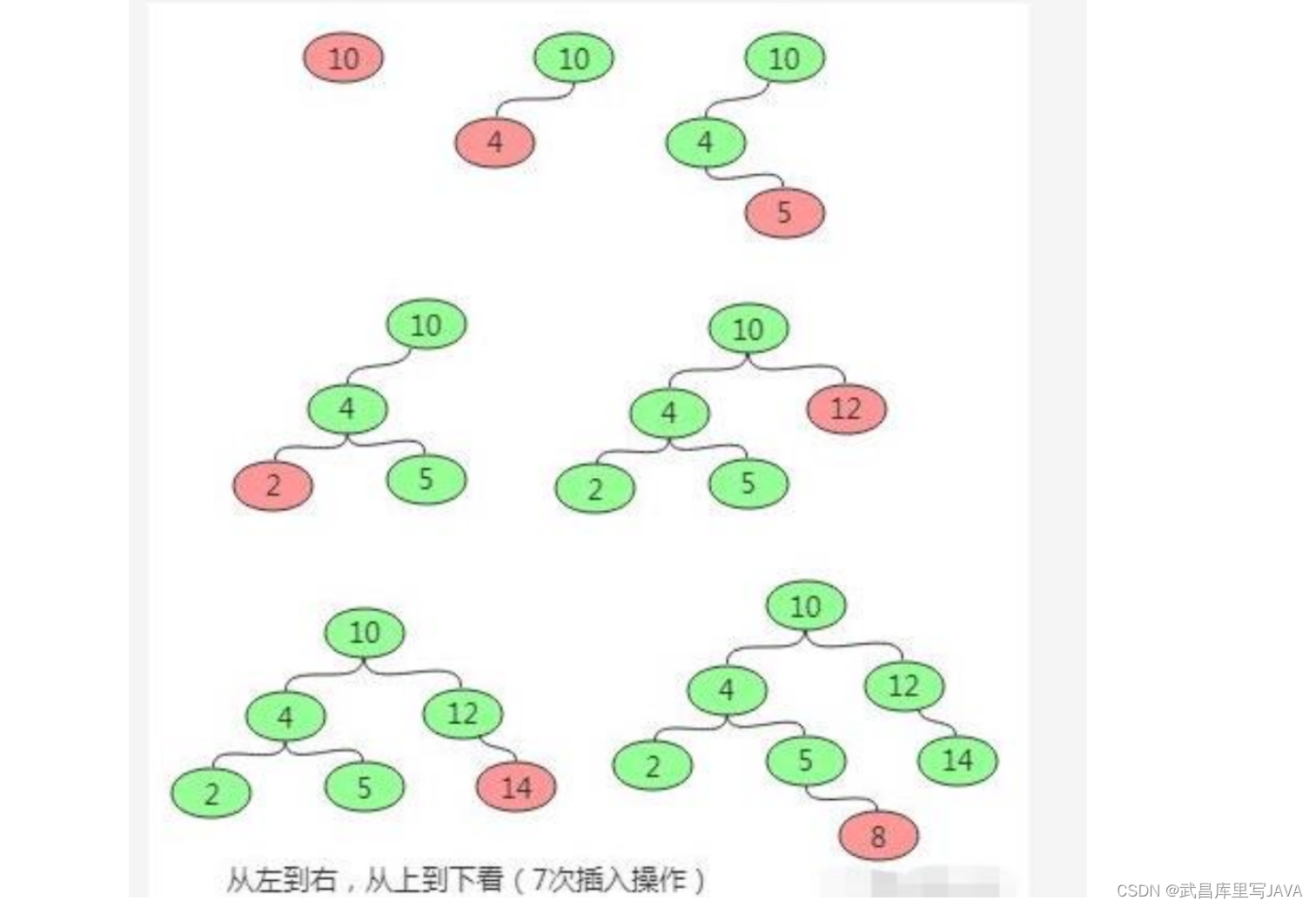
删除操作
删除操作主要分为三种情况,即要删除的节点无子节点,要删除的节点只有一个子节点,要删除的节点有两个子节点。
- 对于要删除的节点无子节点可以直接删除,即让其父节点将该子节点置空即可。
- 对于要删除的节点只有一个子节点,则替换要删除的节点为其子节点。
- 对于要删除的节点有两个子节点,则首先找该节点的替换节点(即右子树中最小的节点),接着替换要删除的节点为替换节点,然后删除替换节点。

查询操作
查找操作的主要流程为:先和根节点比较,如果相同就返回,如果小于根节点则到左子树中递归查找,如果大于根节点则到右子树中递归查找。因此在排序二叉树中可以很容易获取最大(最右最深子节点)和最小(最左最深子节点)值。
遍历操作
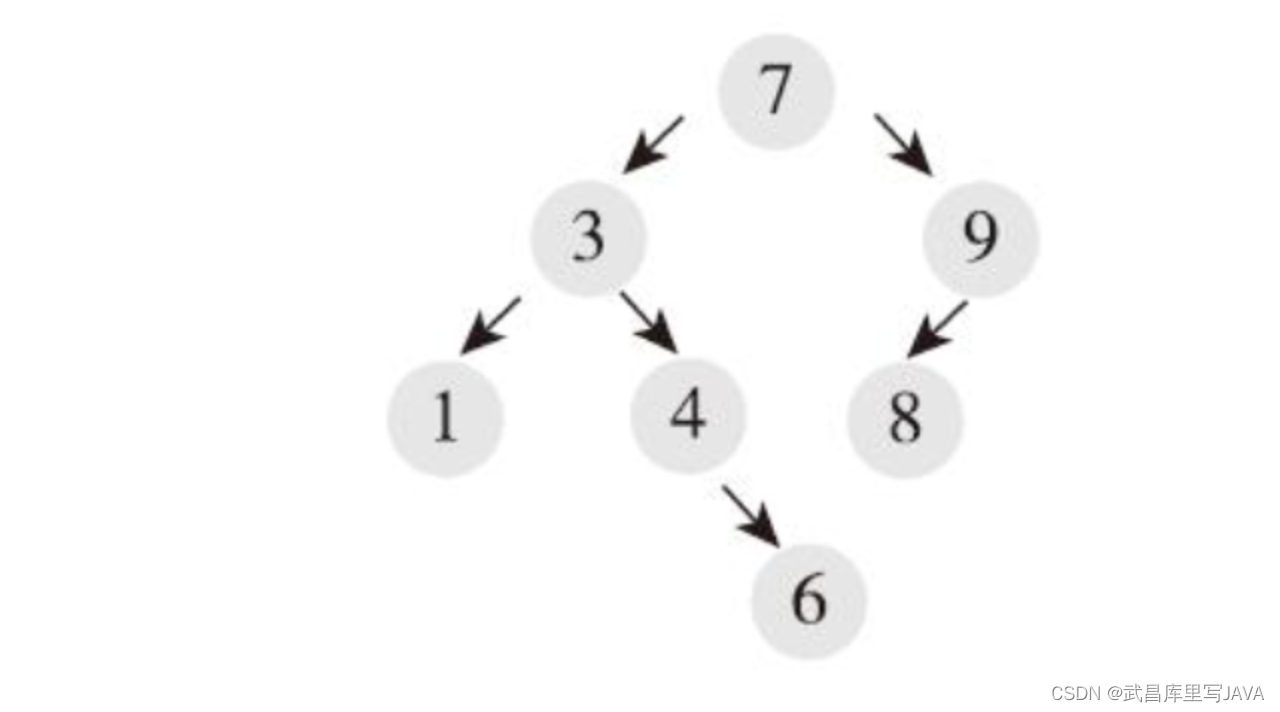
排序二叉树可以方便的按序遍历,用递归的方式。如下图的例子,先访问根节点的左子树,一直到最左边的节点–1,1没有右子树
,返回上一层,访问3,然后访问3的右子树,4没有左子树,所以访问4,然后4的右子树6,以此类推。1–3–4–6–7–8–9
不用递归的方式,也可以实现按序遍历:第一个节点为最左边的节点,从第一个节点开始,依次找后继节点,找其后继节点的算法为:
1)如果该节点有右子节点,则后继节点为右子树中的最小节点;
2)如果该节点无右子节点,则后继节点为父节点或者某个祖先节点,从当前节点往上找,如果它是父节点的右孩子,则继续找父节点,直到它不是右孩子或父节点为空,第一个非右孩子节点的父节点就是后继节点,如果找不到这样的祖先节点,则后继为空,遍历结束。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 用友U8 Cloud smartweb2.RPC.d XXE漏洞复现
- 安全访问服务边缘 (SASE) 增强您公司的网络安全
- iOS 字符串中的字母大小写转换、首字母大写转换
- 1月 mysql索引分享
- Element-ui自定义input框非空校验
- 华为云CodeArts Deploy常见问答汇总
- 蓝牙物联网开发与应用:五大核心应用场景!
- QT 信号与槽
- 【Shell-判断文件是否存在】使用Linux-Shell判断文件或目录是否存在
- 2024最新EasyRecovery易恢复专业数据文件恢复软件