2.1 关系模型的数据结构及形式化定义

2.1.1 关系

单一的数据结构----关系 现实世界的实体以及实体间的各种联系均用关系来表示 。

逻辑结构----二维表 从用户角度，关系模型中数据的逻辑结构是一张二维表 。

建立在集合代数的基础上。

1. 域（domain）

2. 笛卡儿积（Cartesian product）

3. 关系（relation）

1. 域（domain）

域：是一组具有相同数据类型的值的集合。

例: n 整数 n 实数 n 介于某个取值范围的整数 n 长度小于25B的变长字符串集合 n {男，女} n …

2. 笛卡儿积（Cartesian product）

笛卡儿积 ：给定一组域D1，D2，…，Dn，允许其中某些域是相同的。 D1，D2，…，Dn的笛卡儿积为： D1×D2×…×Dn ＝ ｛（d1，d2，…，dn）｜di?Di，i＝1，2，…，n｝，所有域的所有取值的一个组合 ，不能重复。

元组（tuple） ：笛卡儿积中每一个元素（d1，d2，…，dn）叫作一个n元组（n-tuple）或简称 元组。

分量（Component）：笛卡儿积元素（d1，d2，…，dn）中的每一个值di 叫做一个分量。

基数（cardinal number）：一个域允许的不同取值个数 n，若Di（i＝1，2，…，n）为有限集，其基数为mi（i＝1，2，…，n）， 则D1×D2×…×Dn的基数M为：?

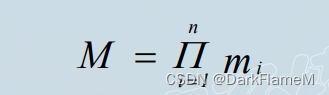
笛卡儿积的表示方法 ：?可表示为一张二维表 n 表中的每行对应一个元组，表中的每列来自一个域。

3. 关系（relation）

关系模型中D1，D2，…，Dn的笛卡儿积一般没有实际语义，只有某个真子集才 有实际含义 。

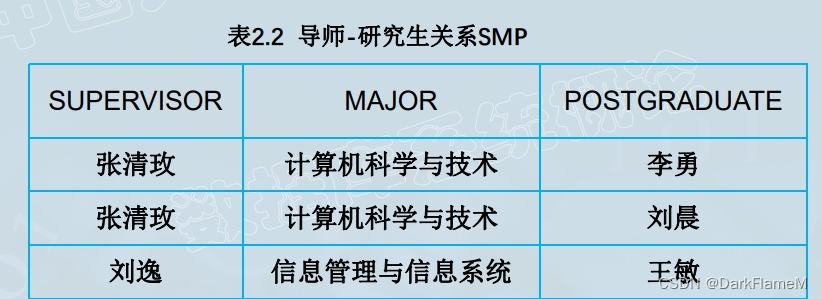
表2.1的笛卡儿积中许多元组是没有意义的 。在学校中一个专业方向有多个导师，而一个导师只在一个专业方向带研究生； 一个导师可以带多名研究生，而一名研究生只有一个导师，学习某一个专业。 ?表2.1中的一个子集才是有意义的，才可以表示导师与研究生的关系，把该关 系取名为SMP。

把关系SMP属性名取为SUPERVISOR，MAJOR和POSTGRADUATE?。

?导 师 - 研 究 生 关 系 模 式 可 以 表 示 为 S M P （ S U P E R V I S O R ， M A J O R ， POSTGRADUATE）。

（2）元组： 关系中的每个元素是关系中的元组，通常用t表示。

（3）单元关系与二元关系：当n=1时，称该关系为单元关系（unary relation） 或一元关系 当n=2时，称该关系为二元关系（binary relation）。

（4）关系的表示：关系也是一个二维表，表的每行对应一个元组，表的每列对应一个域。

（5）属性：关系中不同列可以对应相同的域 n 为了加以区分，必须对每列起一个名字，称为属性（attribute）

（6）三类关系：

基本关系（基本表或基表）：实际存在的表，是实际存储数据的逻辑表示。

查询结果：查询执行产生的结果对应的临时表。

视图表：由基本表或其他视图表导出的虚表，不存储实际数据。

（7）基本关系的性质 ：

① 列是同质的（homogeneous）。

② 不同的列可出自同一个域 ，?其中的每一列称为一个属性 ，不同的属性要给予不同的属性名。

③ 列的顺序无所谓,列的次序可以任意交换。

④ 任意两个元组的码不能相同。

⑤ 行的顺序无所谓，行的次序可以任意交换。

⑥ 分量必须取原子值，即每一个分量都必须是不可分的数据项 这是规范条件中最基本的一条。