LeetCode 98. 验证二叉搜索树

98. 验证二叉搜索树

给你一个二叉树的根节点?root?，判断其是否是一个有效的二叉搜索树。

有效?二叉搜索树定义如下：

• 节点的左子树只包含?小于?当前节点的数。
• 节点的右子树只包含?大于?当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

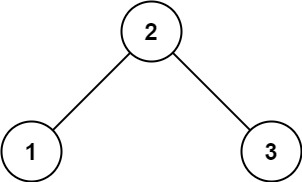
输入：root = [2,1,3]
输出：true

示例 2：

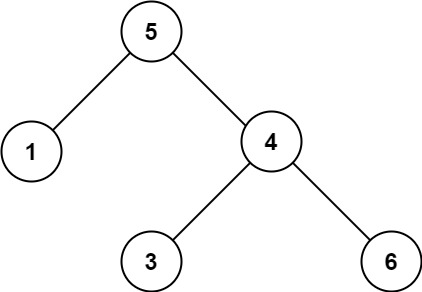
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 10^4]?内
• -2^31 <= Node.val <= 2^31 - 1

解法思路：

1、递归

2、中序遍历

法一：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 * int val;
 * TreeNode left;
 * TreeNode right;
 * TreeNode() {}
 * TreeNode(int val) { this.val = val; }
 * TreeNode(int val, TreeNode left, TreeNode right) {
 * this.val = val;
 * this.left = left;
 * this.right = right;
 * }
 * }
 */
class Solution {
    public boolean isValidBST(TreeNode root) {
        // Recursion
        // Time: O(n) n 为节点数
        // Space: O(n)
        return isValidBSTHelper(root, Long.MIN_VALUE, Long.MAX_VALUE);
    }

    private boolean isValidBSTHelper(TreeNode node, long minVal, long maxVal) {
        // 如果节点为空，视为有效
        if (node == null) {
            return true;
        }
        // 检查当前节点的值是否在合适的范围内
        if (node.val <= minVal || node.val >= maxVal) {
            return false;
        }
        // 递归检查左右子树
        return isValidBSTHelper(node.left, minVal, node.val) && isValidBSTHelper(node.right, node.val, maxVal);
    }
}

法二：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 * int val;
 * TreeNode left;
 * TreeNode right;
 * TreeNode() {}
 * TreeNode(int val) { this.val = val; }
 * TreeNode(int val, TreeNode left, TreeNode right) {
 * this.val = val;
 * this.left = left;
 * this.right = right;
 * }
 * }
 */
class Solution {
    private long prev = Long.MIN_VALUE; // 用于存储前一个节点的值

    public boolean isValidBST(TreeNode root) {
        // Recursion， Inorder Traversal
        // Time: O(n) n 为节点数
        // Space: O(n)
        return inOrderTraversal(root);
    }

    private boolean inOrderTraversal(TreeNode node) {
        if (node == null) {
            return true;
        }
        // 递归遍历左子树
        if (!inOrderTraversal(node.left)) {
            return false;
        }
        // 检查当前节点的值是否大于前一个节点的值
        if (node.val <= prev) {
            return false;
        }
        prev = node.val;
        // 递归遍历右子树
        return inOrderTraversal(node.right);
    }
}