leetcode刷题(剑指offer) 240.搜索二维矩阵Ⅱ
发布时间:2024年01月24日
240.搜索二维矩阵Ⅱ
编写一个高效的算法来搜索 *m* x *n* 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
示例 1:

输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出:true
示例 2:
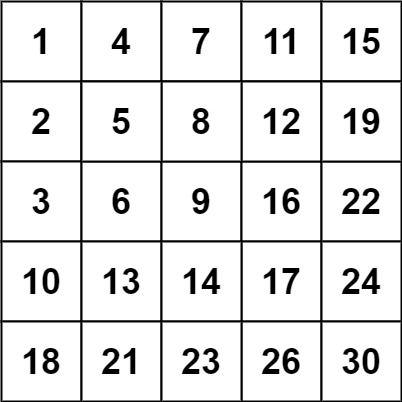
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出:false
提示:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-109 <= matrix[i][j] <= 109- 每行的所有元素从左到右升序排列
- 每列的所有元素从上到下升序排列
-109 <= target <= 109
解法:
仔细观察上图可以发现,从右上角出发,每次往左一格都是更小的数值,每次往下一格都是更大的数值,且从右上角的位置,以往左和往下这两个方向可以抵达二维数组的任何一格。
可能直接从上图的矩阵上来看不容易理解,那么把这个图翻转45°变成下图所示呢。

再加入箭头。。。。。

是不是有点二叉排序树的感觉了。15就是根节点,搜索的次数最多就为这颗树的深度。
从15这个位置开始,如果目标数比15更大就向右,比15更小就向左,以此迭代,最后可以找到目标数,如果遍历到不能再向下遍历了,那就是矩阵中不存在目标数。
方法的时间复杂度为O(N), 空间复杂度为O(1)。
代码如下:
/**
* @author bwzfy
* @ClassName _240搜索二维矩阵
* @create 2024/1/23 - 17:40
* @Version 1.0
**/
public class _240搜索二维矩阵Ⅱ {
private static boolean res = false;
public static void main(String[] args) {
int[][] matrix = new int[][]{
{1, 4, 7, 11, 15},
{2, 5, 8, 12, 19},
{3, 6, 9, 16, 22},
{10, 13, 14, 17, 24},
{18, 21, 23, 26, 30}
};
System.out.println(searchMatrix(matrix, 12));
}
public static boolean searchMatrix(int[][] matrix, int target) {
if (matrix.length == 0 || matrix[0].length == 0) {
return false;
}
int row = 0;
int col = matrix[0].length - 1;
while (row < matrix.length && col >= 0) {
int value = matrix[row][col];
if (target > value) {
row++;
} else if (target < value) {
col--;
} else {
return true;
}
}
return false;
}
}
文章来源:https://blog.csdn.net/weixin_41249051/article/details/135832758
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 2024年程序设计专业的大学毕业生们,怎么写开题报告呢?
- 【webpack5】高级优化
- 用自制编程语言写自制操作系统(二)在空无一人的赛道里狂奔
- count distinct在spark中的运行机制
- 什么叫范数?
- 总结23年最火的前端项目出炉,竟然是它?
- fastapi-amis-admin快速创建一个后台管理系统增加音乐管理功能(3)
- java获取一个视频的时长
- uniapp地图标记点的点击事件
- 定时任务组件Quartz和CronTrigger的介绍和整合SpringBoot项目实例